.原載於科學月刊第十五卷第十二期
.作者當時任教於台大數學系
曹亮吉
|
.原載於科學月刊第十五卷第十二期 .作者當時任教於台大數學系 | |||
|
函數觀念的演變史
曹亮吉 |
|
文藝復興以後,西方的科學觀,可以 Galileo Galilei(1564∼1642年)的看法為代表。他認為大自然是依數學方式建構的,人只要掌握各種現象的基本數學關係,就可以靠數學加以推演。將自然科學數量化,尋求其間的數學關係並加以推演,就成了研究自然科學的新方法。科學革命對數學的影響之一就是促使函數觀念漸趨成熟;當然,函數觀念的成熟也使科學研究帶來許多方便。
Galilei 研究落體運動,發現「物體在空中下降的距離(從靜止開始計算)與所經過時間的平方成正比」、「物體從高度固定的斜板滑落所需的時間與斜板的長度成正比」。也就是說他發現了距離與時間或時間與長度之間的數學關係。距離隨時間而變或時間隨長度而變,用現在的說法就是:距離是時間的函數或時間是長度的函數。研究運動也引出更多的曲線──點動成曲線,而曲線和函數之間,也經由解析幾何的引入,變得不可分離。
用坐標的方法研究曲線,就是把曲線以 x、y 的關係式表示,然後用代數的方法加以處理。反過來,如果採取 Fermat 式的解析幾何觀,從任何一個 x、y 的關係式出發,探討它所代表的曲線的幾何性質,那麼函數觀念的重要性更顯而易見了,因為 x、y 之間的關係常以函數的方法出現。
函數到底是什麼呢?最早的想法認為:一個函數是一個代數式子,只含變數以及加減乘除開方等符號,漸漸地,所謂超越(代數的)函數,如
為了求得一個函數的導數,Newton(1642∼1727年)儘量把函數寫成冪級數,譬如,為了求得
而得 因此當 h 趨近於 0 時,就得 到了十八世紀,數學家乾脆認定函數就是冪級數。譬如 則 因此當 x 趨近於 0 時,就得 f'(x0) = a1。由此可以導出:一個函數(冪級數)各項的微分和就是原函數的微分;反過來,一個函數各項的積分和就是原函數的積分。這麼一來,函數的微積分變得非常簡單;當然他們忽略了冪級數的收斂問題。
「函數就是冪級數」是十八世紀眾所公認的觀念,但波動問題的興起,使得這種觀念不時遭到挑戰,迫使 Euler(1707∼1783年)也承認:最先開始時,弦所成的曲線 y=f(x) 可以是任意的,只要是連續的,但不一定可以用冪級數來表示。到了 Fourier(1768∼1830年)研究熱傳導時,他發現他必須把初期條件函數 f(x) 以三角級數的方式展開:

而 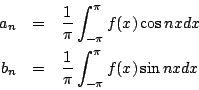
根據傳統的做法,他原假定 f(x) 為冪級數才能得到這樣的表示法,但他注意到an、bn 只不過是函數 的曲線之下的面積而已,所以不管 y=f(x) 是怎樣的曲線,an、bn 都可以計算而得。他試了種種的函數 f(x),求取頭幾個 an、bn 的值,發現將由此而得的三角級數頭幾項和所代表的曲線與原來的曲線 y=f(x) 相比較,都相當接近。所以 Fourier 深信「任何」函數 f(x) 都可以表成三角級數之和。
三角級數的興起引起了函數觀念的再檢討。譬如在
若 x 在
推而廣之,可以分段用熟知的式子表示者也可以看成函數,在十八世紀時很少人會有這樣的認識。
Fourier 宣稱「任何」函數都可以表成三角級數之和的看法更值得檢討,因為到底什麼是函數,Fourier 也說不清楚。函數觀念的澄清是 Dirichlet(1805∼1859年)研究 Fourier 論之後的重要貢獻之一。他認為 y=f(x) 是個函數的意思是說:f 是一個規則,它告訴我們說,變數 x 之值固定了,其相應唯一的 y 值是什麼。f 不一定要是個式子,它只要能說清楚 x 到 y 之間的對應是什麼就好了。有了 Dirichlet 的函數觀念,數學家才能談什麼時候 an、bn 之值可以確定,什麼相對應的三角級數在特定的區間內和原來的函數是一致的。
雖然 Dirichlet 有了函數最一般的定義,通常我們總希望用式子來表示一個函數所提供的規則。但什麼是式子呢?譬如,我們都承認 f(x)=x2+x+1 是個式子;其實它代表一段敘述,告訴我們函數對應的規則:把變數 x 自乘,加上變數本身,再加上 1,就是變數對應的 y 值。只因我們太習慣多項式所代表的意義,所以認為它是個式子,而不認為它代表的是一段敘述。再如
除了「明」的式子外,還有些「暗」的式子。暗的式子指的是以參數函數、隱函數、微分方程式、積分方程式等來表示自變數 x 與他變數 y 之間的數學關係。怎樣化暗為明自然是最重要的課題之一。
式子之外,函數最常以曲線的形式出現。當然,每當有曲線出現,數學家總是想辦法把它量化,以式子的形式表示,好方便研究。譬如行星運行的軌道,是個橢圓其(隱)函數為
又譬如小提琴聲波呈現規則而複雜的形狀(見圖三),它可以表成一三角級數。
當然並不是每條曲線都能找到適當的式子。譬如如某地的氣溫變化曲線,患病者的腦波(見圖四)等等這些太不規則的曲線恐怕就很難用式子表示。
Dirichlet 曾經考慮過有理數的特徵函數,它在有理數時取值為 1,否則為 0。這樣的函數根本無法用圖形來表示。
Weierstrass(1815∼1897年)曾經提出一個級數函數
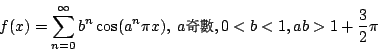
它是個連續的,但到處不可微分的函數。用曲線的觀點來看,它是個連續不斷,一整條的,但又到處沒有切線的曲線。這樣的曲線是用圖畫不出來的。別以為這是古怪的曲線,Wiener(18944∼1964年)證明:幾乎所有的分子的 Brown 運動的路徑都是連續而到處沒有切線的。
Dirichlet 的函數觀不但包含已往種種的函數,提供了許許多多新鮮有趣、有用的例子,而且也因為函數觀念的確定,使得數學家能夠討論函數的連續、微分、積分等種種有關的性質。經過幾世紀的發展,函數成為數學中最基本的觀念之一,同時也是科學數量化的主要工具。
|
對外搜尋關鍵字: .Galileo .Fermat .Newton .冪級數 .Euler .Fourier .三角級數 .Dirichlet .Bessel函數 .Legendre多項式 .參數函數 .隱函數 .微分方程式 .積分方程式 .曲線 .懸垂線 .Weierstrass .Wiener .Brown運動 .連續 .微分 .積分 .Leibniz |
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:洪瑛 / 校對:黃信元 / 繪圖:簡立欣 | 最後修改日期:2/17/2002 |