|
在談積分之前,不得不複習所謂微量的概念。任何一個量都容許些微的變動,比方說,時間是一個量,在某時刻 t 的時候,可以讓 t 再往前走一點點,或者,(假想)往後走一點點,這個「一點點」就是一個微量,通常記成 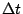 , ,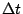 可正可負,它的值不必確定,它可以是千分之一、萬分之一、或是更小更小。一般而言,現象通常以一個或多個量來描述,例如在 t 時刻時,某物的位置在 x,或是當密度為 ρ 的時刻,某物所受的浮力為 F 等等。當我們觀察兩個相關的量的時候,其中一個量微微的變化,會影響另一個量也跟著起了微微的變化,也就是說,這兩個微量(的變化)之間是相關的。由於生活中一些具體事物的啟發,我們因此專注在理解兩個微量之間的比值。
比方說 可正可負,它的值不必確定,它可以是千分之一、萬分之一、或是更小更小。一般而言,現象通常以一個或多個量來描述,例如在 t 時刻時,某物的位置在 x,或是當密度為 ρ 的時刻,某物所受的浮力為 F 等等。當我們觀察兩個相關的量的時候,其中一個量微微的變化,會影響另一個量也跟著起了微微的變化,也就是說,這兩個微量(的變化)之間是相關的。由於生活中一些具體事物的啟發,我們因此專注在理解兩個微量之間的比值。
比方說
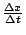 ,又由於 ,又由於 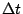 的大小並不確定,我們因此發展了一個令 的大小並不確定,我們因此發展了一個令 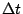 趨近於 0 的(求極限)處理方式,記成 趨近於 0 的(求極限)處理方式,記成
稱為 x 對 t 的微分。如果了解求微分的操作,就可以從已知的公式中,如
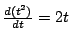 ,得到當 x=t2 時, ,得到當 x=t2 時,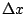 和 和 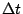 的比之極限是 2t。在更多的場合,我們常常喜歡使用另一種寫法,即 d(t2)=2tdt,或 d(x2)=2xdx(參見〈條目:微分〉)。 的比之極限是 2t。在更多的場合,我們常常喜歡使用另一種寫法,即 d(t2)=2tdt,或 d(x2)=2xdx(參見〈條目:微分〉)。
如果兩個量 y 與 x 之間有 y=x2 的關係,那麼,從 d(x2)=2xdx 這個關係式中,y=x2 對 x 的微分就是 2x,經常,我們把上述的觀念直接表成
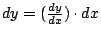 。或者,如果 y=f(x),dy=f'(x)dx。 。或者,如果 y=f(x),dy=f'(x)dx。
式子
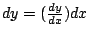 千萬不可看成只是把「dy」除以「dx」再乘以「dx」,而應該讀成「將 千萬不可看成只是把「dy」除以「dx」再乘以「dx」,而應該讀成「將 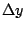 與 與 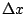 之比的極限表成 之比的極限表成 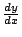 」或者「dy 與 dx 之比就是 y 對 x 的微分,記成 」或者「dy 與 dx 之比就是 y 對 x 的微分,記成 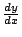 」。 」。
積分,則是一個把許多微量重新求和的概念。例如,想求圓的面積 A,如果把圓割成許多小小的扇形,這每一個小小的扇形可以籠統的以 dA 表達。在分割的過程中,無論分成多麼細的扇形,它們的總和總是原來的 A 這個量,記成 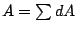 或 或 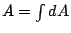 , ,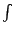 是 是 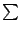 的變形,它代表對無窮多個無窮小的微量求和的過程。 的變形,它代表對無窮多個無窮小的微量求和的過程。
再說,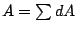 也不能簡單的看成是一句廢話,這個式子有兩個要緊之處,其一就是剛才談過的「A 是一個不變的總量」這件事,任何一個問題的處理,都要注意到所求的量是不會因為求法的不同而改變的。其二就是 也不能簡單的看成是一句廢話,這個式子有兩個要緊之處,其一就是剛才談過的「A 是一個不變的總量」這件事,任何一個問題的處理,都要注意到所求的量是不會因為求法的不同而改變的。其二就是 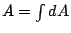 的這個表示,必須要倚重另一個量才有真正的用處。例如弧長 s,我們知道一個小扇形可以看成是一個小小的等腰三角形,它的底邊近似來看是 ds 而腰或高的近似就是半徑 r,因此 的這個表示,必須要倚重另一個量才有真正的用處。例如弧長 s,我們知道一個小扇形可以看成是一個小小的等腰三角形,它的底邊近似來看是 ds 而腰或高的近似就是半徑 r,因此
這樣一個表示同時也提醒我們 dA 和 ds 這兩個微量之間的關係,這個關係是從本文一開始就一再強調的。
知道了
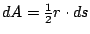 ,則 ,則 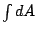 就是 就是 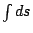 的 的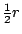 倍,但是 倍,但是 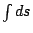 的意義正是求所謂圓周的總長,因此得到圓面積的公式 的意義正是求所謂圓周的總長,因此得到圓面積的公式
我們注意到,如果不能把 dA 表達成另一個微量 ds 的一個係數,那麼即便是寫下 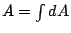 也是無法真正求出一個答案來。 也是無法真正求出一個答案來。
可以這麼說,若是想求一個量 Q,積分的意義就在於把 Q 表成 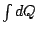 之後,再繼續把 dQ 以某一個更方便的微量 dP 來表成 之後,再繼續把 dQ 以某一個更方便的微量 dP 來表成
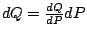 ,則 ,則
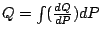 ,如果能了解 ,如果能了解 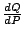 ,就可以掌握 Q,這樣的想法和過程不僅幫我們求出答案,同時,也說明了求 Q 的方式不外是了解 ,就可以掌握 Q,這樣的想法和過程不僅幫我們求出答案,同時,也說明了求 Q 的方式不外是了解 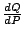 再得到 Q,這個過程有人說成是求 再得到 Q,這個過程有人說成是求 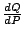 的反微分,因為 的反微分,因為 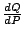 是 Q 的微分,所以 Q 就是 是 Q 的微分,所以 Q 就是 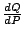 的反微分了。至於求 Q 的時候要選誰當(參考量)P 呢?那當然要看哪一個 P 才能提供最清楚的 的反微分了。至於求 Q 的時候要選誰當(參考量)P 呢?那當然要看哪一個 P 才能提供最清楚的 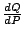 。
一般來說,問題的本身可能會提供不只一個的參考量 P,但是若是不能方便的知道 。
一般來說,問題的本身可能會提供不只一個的參考量 P,但是若是不能方便的知道 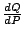 ,如何求 Q 也就幫不上忙。 ,如何求 Q 也就幫不上忙。
再以求 y=f(x) 的函數圖形下所覆蓋的面積 A 為例,如果以 x 為參考量的話,要如何理解 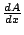 呢?注意到 呢?注意到 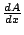 是 是
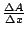 的極限,也就是說要先了解當 x 變化到 的極限,也就是說要先了解當 x 變化到 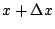 時,A 究竟起了什麼變化?當然 時,A 究竟起了什麼變化?當然 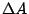 是一個近似的梯形,它的高是 是一個近似的梯形,它的高是 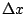 ,下底和上底分別是 y 和 ,下底和上底分別是 y 和 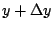 ,同時面積 ,同時面積 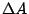 近似等於 近似等於
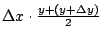 ,而 ,而
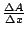 近似等於 近似等於
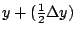 ,當 ,當 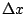 趨近於 0,得到 趨近於 0,得到
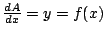 ,所以求 A 等於是求 y=f(x) 的反微分,這正是牛頓與 Leibniz 發現的微積分基本定理。 ,所以求 A 等於是求 y=f(x) 的反微分,這正是牛頓與 Leibniz 發現的微積分基本定理。
|