蜜蜂與數學 (第 4 頁)

　1│2│3│4│5│6　

蜜蜂與數學（第 4 頁）

蔡聰明

首頁 | 搜尋

．原載於科學月刊第二十七卷第七期
．作者當時任教於台大數學系
‧對外搜尋關鍵字

蜂巢的極值原理

自古以來，人類對於蜜蜂的勤勞以及蜂巢的巧妙精準，無不讚揚有加。從生物學的祖師爺亞里斯多德 (Aristotle)，到數學家 Pappus，以及近代的博物學家達爾文 (Darwin) 都曾留下讚美的語句。

工蜂分泌蜂蠟築成蜂巢，做為后蜂產卵、育幼，以及存放蜂蜜、花粉的儲藏室。從正面看起來，蜂巢是由許多正六邊形的中空柱狀儲藏室連結而成，參見圖八，讀者若具有實地見過蜂巢的經驗當然是最好。

圖八

從整個立體的蜂巢來看，它具有左右（或前後）兩側的儲藏室．其截面如圖九；而圖十是一個柱狀的儲藏室，其底部是由三個全等的菱形面 ASBR、ASCQ與 PBSC 所組成。

圖九

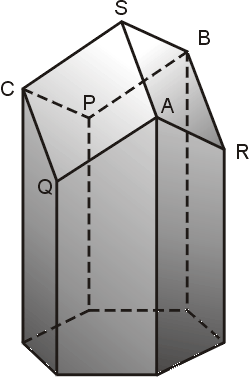
圖十

人類對於蜂巢的結構，由觀察產生驚奇，進而提出兩個數學問題：

(i): 為何是正六邊形？
(ii): 底邊為何是三個全等的菱形面組成？

下面我們就來探索這兩個問題。

第一個問題涉及古老的等周問題 (isoperimetric problem)：即在平面上，要用固定長的線段圍成一塊封閉的領域，使其面積為最大，問應如何圍法？

這個問題又叫做 Dido 問題。在古希臘傳說中，Dido 公主（建立迦太基的女王）憑她的直覺提出正確的答案：圓。不過，要等到兩千多年後的十九世紀，透過變分學 (calculus of variation) 的研究，才有真正嚴格的證明。

對於等周問題，古希臘數學家 Zenodorus（約180 B.C.）已經證得下列的結果：

: (i) 在所有 n 邊形中，以正 n 邊形的面積為最大，並且邊數越多，面積也越大；
: (ii) 圓的面積比任何正多邊形的還要大。

另外一方面，古埃及人已經知道，用同一種形狀與大小的正多邊形舖地，恰好只有三種樣式，參見圖十一。

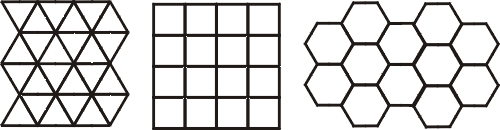
圖十一

即只能用正三角形，正方形與正六邊形三種情形，再沒有其他的了。這是三角形三內角和為 180°的簡單推論。

蜜蜂分泌蜂蠟築巢，從橫截面來看，這相當於是用固定量的蠟，要圍成最大的面積，這是等周問題。由 Zenodorus 的結果，再配合上述舖地板只有三種樣式，所以蜜蜂只有正三角形、正方形與正六邊形三種選擇，而蜜蜂憑本能選擇了最佳的正六邊形。換言之．蜜蜂採用「最經濟原理」來行事。

亞歷山卓 (Alexandria) 的幾何學家 Pappus，約在西元300年出版一套八冊的《數學文集》(Mathematical Collection)，其中第五冊討論等周問題及蜂巢結構問題。他特別稱讚蜜蜂「依本能智慧作論證」(reason by instinctive wisdom) 的本領，天生俱有的「某種幾何的洞悟力」(a certain geometrical foresight)。

其次，我們探討蜂巢的第二個問題，即每個儲藏室 (cell) 底部的幾何結構。這個問題比較困難。

我們觀察蜂巢的一個儲藏室，它是中空的正六角形柱，而底部是由三個菱形面組成，交會於底部中心頂點 S（見圖十二）。讓我們先回顧一段歷史。

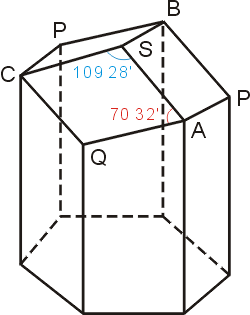
圖十二

在1712年，巴黎天文觀測所的天文學家 G.F. Maraldi，他實際度量菱形的角度，得到的結果是 70°32' 與 109°28'，見圖十二。Maraldi 實地叩問自然，並且相信蜜蜂是根據單純 (simplicity) 與數學美 (mathematical beauty) 兩個原理來築巢。

Maraldi 的結果引起法國著名的博物學家 Reaumur 的興趣，他猜測蜜蜂選擇這兩個角度一定是有原因的，可能就是要在固定容積下，使得表面積為最小，即以最少的蜂蠟作出最大容積的儲藏室。因此，Reaumur 就去請教瑞士年輕的數學家 Samuel König 如下的問題：

給定正六角形柱，底部由三個全等的菱形作成，問應如何做會最節省材料？

Reaumur 並沒有告訴 König 這個問題是由蜂巢引起的。

一直等到 König 把算得的結果 70°34" 與 109°26" 送到 Reaumur 的手裡，Reaumur 才告訴 König 關於蜂巢與 Maraldi 的實測結果。他們對於理論與實測的結果僅相差 2"，同感震驚。König 的結果支持了 Reaumur 的猜測：蜜蜂是按「最經濟原理」來行事。König 利用微分法解決上述的極值問題，他說：「蜜蜂所解決的問題，超越古典幾何的能力範圍，而必須用到 Newton 與 Leibniz 的微積分。」然而，一代博學者 Fontenelle（法國科學院永久秘書）在1739年卻作出著名的判斷，他否認蜜蜂具有智慧，認為蜜蜂只是按照天生自然與造物者的指示，「不知亦能行」地（盲目地）使用高等數學而已。

關於 König 的相差2分問題，後來經過 Cramer、Boscovich、Maclaurin 等人的重算，發現蜜蜂是對的，錯在 König，而 König 所犯的小錯又出在計算 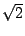$\sqrt{2}$ 時，所使用的數值表印錯了一個數字。

下面我們就來求解 Reaumur 對 König 所提出的極值問題。

考慮圖十三的正六角形柱，在 A、C、E 處分別用平面 BFM、BDO、DFN 截掉三個相等的四面體 ABFM、CDBO、EDFN，見圖十四，使得變成圖十五。三個平面 BFM、BDO、DFN 延伸交於頂點 P，見圖十六。從圖十三變成圖十六，所截掉的體積恰好等於所補足的體積。因此，圖十三與圖十六的體積相等，但是，兩者的表面積卻不相等。

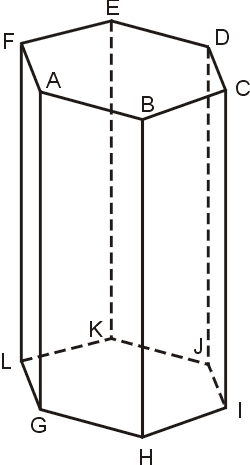
圖十三

因此，原極值問題等價於，在容積固定下，求最小表面積。蜂巢一個儲藏室的表面（圖十六）是由六個梯形（BMGH 等等）與三個菱形組成的。在圖十四中，設AB=a，BH=h，AM=x（x 是變數），則由餘弦定律與畢氏定理可求得菱形PBMF 的對角線

$\begin{displaymath} BF=\sqrt{3}a \quad, \quad MP=2\sqrt{x^2+\frac{a^2}{4}} \end{displaymath}$

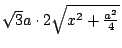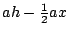今每個菱形的面積為 $\sqrt{3}a\cdot 2\sqrt{x^2+\frac{a^2}{4}}$ 每個梯形的面積為 $ah-\frac{1}{2}ax$ ，所以一個儲藏室的總表面積為

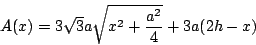$\begin{displaymath} A(x) = 3\sqrt{3}a\sqrt{x^2+\frac{a^2}{4}}+3a(2h-x) \end{displaymath}$

(5)

由微分法，令 A'(x)=0 得

$\begin{displaymath}3\sqrt{3}ax\cdot\frac{1}{\sqrt{x^2+\frac{a^2}{4}}}-3a=0\end{displaymath}$

解得

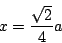$\begin{displaymath} x=\frac{\sqrt{2}}{4}a \end{displaymath}$

(6)

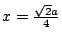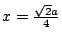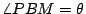利用二階微分，容易驗知 $x=\frac{\sqrt{2}a}{4}$ 確是極小點。在 $x=\frac{\sqrt{2}a}{4}$ 之下，進一步令菱形的銳角 $\angle PBM=\theta$ ，則

$\begin{displaymath}\tan(\frac{1}{2}\theta)=\frac{\sqrt{2}}{2}\end{displaymath}$

從而

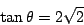$\begin{displaymath} \tan\theta &=& 2\sqrt{2} \end{displaymath}$

(7)

$\begin{displaymath} && \theta \quad \mbox{{\fontfamily{cwM2}\fontseries{m}\selec... ...{cwM1}\fontseries{m}\selectfont \char 107}} \quad 70^\circ 32' \end{displaymath}$

習題：在圖十六中，令 α 表示對角線 PO 與中心軸 PQ 之交角，試證一個儲藏室的總表面積為

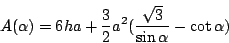$\begin{displaymath} A(\alpha)=6ha+\frac{3}{2}a^2(\frac{\sqrt{3}}{\sin\alpha}-\cot\alpha) \end{displaymath}$

(8)

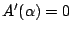再解 $A'(\alpha)=0$ ，得

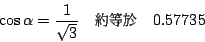$\begin{displaymath} \cos\alpha=\frac{1}{\sqrt{3}} \quad \mbox{{\fontfamily{cwM2}... ...family{cwM1}\fontseries{m}\selectfont \char 107}}\quad 0.57735 \end{displaymath}$

(9)

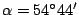
所以 $\alpha=54^\circ 44'$

註：我們也可以利用(6)式，再配合圖十六，推得(9)式。

對於一個初等的極值問題，要用到微分法來處理（殺雞用牛刀），令人不滿意。於是有人，例如 Maclaurin（1743）、L'Huillier（1781），開始尋求初等的、簡單的代數與幾何解法。

(i)代數的配方法
我們注意到，在上述的解法中，其實都跟 a 與 h 無關，所以我們不妨從頭就假設 a=1。於是(5)式變成

$\begin{displaymath}A(x)=3\sqrt{3}\sqrt{x^2+\frac{1}{4}}+6h-3x\end{displaymath}$

由於 6h 是常數，故只需求

$\begin{displaymath}f(x)=\frac{3\sqrt{3}}{2}\sqrt{1+4x^2}-3x\end{displaymath}$

之最小值。令

$\begin{eqnarray*} y &=& \frac{3\sqrt{3}}{2}\sqrt{1+4x^2}-3x \\ y+3x &=& \frac{3\sqrt{3}}{2}\sqrt{1+4x^2} \end{eqnarray*}$

兩邊平方，再化簡得

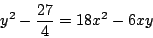$\begin{displaymath} y^2-\frac{27}{4} &=& 18x^2-6xy \end{displaymath}$

(10)

對右項配方，再化簡得

$\begin{displaymath}3y^2-\frac{27}{2}=(6x-y)^2\geq0\end{displaymath}$

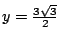因此，當 y=6x 時，y 有最小值 $y=\frac{3\sqrt{3}}{2}$ ，從而

$\begin{displaymath}x=\frac{y}{6}=\frac{\sqrt{2}}{4}\end{displaymath}$

得到跟 (6)式相同的答案（a=1）。

(ii)二次方程的判別式法
由(10)式得

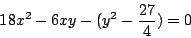$\begin{displaymath} 18x^2-6xy-(y^2-\frac{27}{4})=0 \end{displaymath}$

(11)

看作是 x 的二次方程式。因為 x 恒為實數，故(11)式的判別式

$\begin{displaymath}\Delta=36y^2+4\times 18 \times(y^2-\frac{27}{4})\geq0\end{displaymath}$

整理化簡得

$\begin{displaymath}y^2\geq\frac{9}{2}\end{displaymath}$

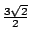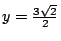於是 y 的最小值為 $\frac{3\sqrt{2}}{2}$ ，以 $y=\frac{3\sqrt{2}}{2}$ 代入(11)式得

$\begin{displaymath}x=\frac{\sqrt{2}}{4}\end{displaymath}$

達爾文稱讚蜂巢為「在已知的僅憑本能的建構中是最令人驚奇的成就」。他又說：「欲超越這樣完美的建構，自然選擇 (natural selection) 是不能達成的，因為就我們所見，蜂巢不論是在勞動力上或蜂蠟的使用上，都符合最經濟的原則，是絕對地完美。」

在大自然中，除了蜜蜂遵行「最小原理」之外，還有荷葉上的水珠，校園草地出現的人行道，光的 Heron 最短路徑原理與 Fermat 的最短時間原理等等，這不禁使我們要猜測，大自然是按著某種「最小原理」來運行的。

在十七世紀，Leibniz 從哲學上論證「這是所有可能世界中最好的一個世界」(the best of all possible worlds)。物理學家終於在十八、十九世紀找到了動力學的「最小作用量原理」(the principle of least action)，成為數理科學中最美麗的成就。

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：黃信元

最後修改日期：2/27/2002