蜜蜂是群居性的昆蟲,嚴格施行分工合作的社會(經濟學家 Adam Smith 在1776年才開始提倡人類社會也應該分工合作)。一個蜂巢通常是由一隻后蜂(又叫蜂王,是體型最大的雌蜂)、約五萬隻的工蜂以及數百隻的雄蜂組成的。后蜂專司產卵,是蜂群共同生活中心;工蜂負責築巢、清潔、採蜜、分泌蜂王乳、守衛、餵食幼蜂等工作;雄蜂是「小白臉」,好吃懶做,只負責跟后蜂交配。受精卵孵化出雌蜂之幼蟲,若持續餵以蜂王乳就長成蜂王;若前三天餵以蜂王乳,以後餵以蜂蜜或花粉,就發育成工蜂,因此工蜂是雌蜂。后蜂所產的未受精卵就孵化為雄蜂,故雄蜂有母無父,這是奇特之處。參見圖一。

圖一
|
採蜜是工蜂最繁重的工作。首先是派出一些工蜂做偵察蜂 (explorer),到處去找尋蜜源。當偵察蜂發現採蜜的地點時,回巢要如何告知同伴呢?這就是描述地點的問題。蜜蜂不會說話,如何解決這個難題呢?
我們人類描述地點的方式有很多種,例如從日常生活用語言說明、用手明指方向、畫張地圖、給出你家的地址、說出颱風所在的經緯度,到數學上更有效的直角坐標、極坐標、柱坐標、球坐標、廣義坐標等等。
然而蜜蜂沒有「語言」,怎麼辦呢?牠們有「跳舞語言」(the dance language),以跳舞的方式來傳遞訊息,描述地點,基本上就是極坐標!(我們不要受人類自己習以為常的「語言」框框所限制!)
奧地利動物學家 Karl von Frisch(1886∼1982)就是專門研究蜜蜂的跳舞語言與定向 (orientation) 而有成的人,他懂得「蜂語」,故被譽為「現代公冶長」(公冶長聽得懂「鳥語」)。由於對個別動物及其社會行為規律的研究有卓著的貢獻,Frisch 與德國的 Konrad Lorenz、荷蘭的 Nikolaas Tinbergen 在1973年一起得到諾貝爾生理學暨醫學獎。
根據 Frisch 的研究,當偵察蜂發現一處蜜源時,牠飛回巢就先放出氣味,並且在垂直的蜂巢表面上跳舞。基本上分成兩種舞步:圓舞與搖尾舞。
如果蜜源距離蜂巢超過100公尺,則跳搖尾舞。先走一小段直線路徑,再繞半圓,回到原出發點,然後走原直線路徑,再對另一側繞半圓,如此規律地反覆交替繞半圓。在走直線路徑時,還不斷地搖擺牠的下腹,這是「搖尾舞」名稱的由來。
圖二
|

圖三
|
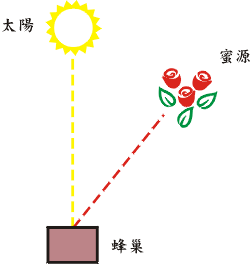
如果太陽、蜂巢與蜜源的位置關係如圖二所示,那麼圖三就是相應的搖尾舞,其中有四隻尾隨者接到訊息(見參考資料1,p.57)。直線路徑偏離鉛垂線右方30度,這表示蜜源在太陽方向偏右30度的方向。至於蜂巢與蜜源的距離由單位時間的繞圈數決定,繞越多圈表示距離越遠。例如,每分鐘若繞18圈,就表示距離約為1000公尺。如果直線路徑垂直向上的話,就表示蜜源在太陽的方向。因此,我們看出偵察蜂並不是使用直角坐標,而是採用極坐標來傳遞訊息。鳥類與魚類也有類似的行為。
所謂極坐標就是,為了描述平面上 P 點(蜜源)的位置,於是在平面上選定一條半線
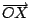 (蜂巢與太陽方向之半線),叫做極軸,O 點叫做極點(蜂巢),將極軸旋轉一個角度 θ,遇到 P 點, (蜂巢與太陽方向之半線),叫做極軸,O 點叫做極點(蜂巢),將極軸旋轉一個角度 θ,遇到 P 點,
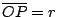 ,那麼 P 點的極坐標就是 (r,θ),參見圖四。在極坐標的世界有許多美妙的幾何圖形,例如各種螺線、擺線(輪迴線)等,這些都是直角坐標方程式難於表達的。 ,那麼 P 點的極坐標就是 (r,θ),參見圖四。在極坐標的世界有許多美妙的幾何圖形,例如各種螺線、擺線(輪迴線)等,這些都是直角坐標方程式難於表達的。
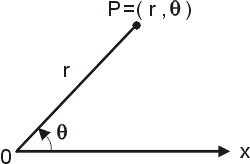
圖四
|
如果蜜源在100公尺以內,偵察蜂就跳圓舞,參見圖五。這表示蜜源就在附近,請同伴出去四周圍轉一下就可以找到。實際上,在圓舞與搖尾舞之間還有一些變化形狀,在此就略掉不提。
圖五
|
由下面的數據我們可以體會到工蜂的辛苦與勤勞。工蜂採集10公斤的花蜜才能釀造出半公斤的蜂蜜,而工蜂必須出動八萬次,每次平均飛行兩公里才能採集到10公斤的花蜜。換言之,每釀造1公斤的蜂蜜,必須飛行32萬公里,大約是繞地球8圈的距離。
Frisch 的主要工作如下:在1910年證明魚可以看出不同的顏色;1919年發現蜜蜂透過身體的搖動來傳遞訊息;在1947年發現蜜蜂利用極化光來定向。他更在1967年出版《蜜蜂的跳舞語言與定向》一書(即參考資料1)。物理學家李政道曾說,他喜讀各種雜書,其中 Frisch 的這本名著就是他覺得特別有趣的一本。
|