瓦里斯公式及其相關的結果 (第 3 頁)

　1│2│3│4│5│6│7　

瓦里斯公式及其相關的結果（第 3 頁）

蔡聰明

首頁 | 搜尋

．原載於科學月刊第二十七卷第五期
．作者當時任教於台大數學系
‧對外搜尋關鍵字

瓦里斯、史特林公式的等價性

在組合學裡，有一個重要的公式叫做史特林公式 (Stirling formula)：

$\begin{displaymath}n!\sim\sqrt{2\pi n} n^ne^{-n}\eqno{(13)}\end{displaymath}$

此式的意思是指

$\begin{displaymath}\lim_{n\rightarrow\infty}\frac{n!}{\sqrt{2\pi n} n^ne^{-n}}=1\eqno{(14)}\end{displaymath}$

亦即當 $n \rightarrow \infty$ 時，n! 與 $\sqrt{2\pi n} n^ne^{-n}$ 漸近地相等(asympotically equal)。史特林公式的由來，請見參考資料[2]。

令人驚奇的是史特林公式居然跟瓦里斯公式等價 (equivalent)，本段我們就來證明這件事。

(一)瓦里斯公式的各種變形

瓦里斯公式(1)就是

$\begin{displaymath}\frac{\pi}{2}=\lim_{n\rightarrow\infty}\frac{2\cdot2\cdot4\cd... ...ts2n\cdot2n}{1\cdot3\cdot3\cdot5\cdots2n-1\cdot2n-1}\eqno{(15)}\end{displaymath}$

這個式子可以有三種等價的變形：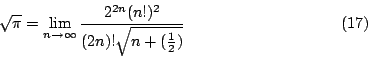

$\begin{displaymath}\pi=\lim_{n\rightarrow\infty}(\frac{2}{1})^2\cdot(\frac{4}{3})^2\cdots(\frac{2n}{2n-1})^2\cdot\frac{2}{n+1}\eqno{(16)}\end{displaymath}$

$\begin{displaymath}\sqrt{\pi}=\lim_{n\rightarrow\infty}\frac{2^{2n}(n!)^2}{(2n)!\sqrt{n+(\frac{1}{2})}}\eqno{(17)}\end{displaymath}$

$\begin{displaymath}\sqrt{\pi}=\lim_{n\rightarrow\infty}\frac{2^{2n}(n!)^2}{(2n)!\sqrt{n}}\eqno{(18)}\end{displaymath}$

這些也都叫做瓦里斯公式。

上述(17)與(18)兩式的等價性所根據的理由是：若 $\lim_{n \rightarrow \infty} a_n = \alpha$ 且 $a_n \sim b_n$ ，則 $\lim_{n \rightarrow \infty}b_n = \alpha$ 。這可以利用極限的 $\epsilon-N$ 式加以證明。

(二)由史特林公式證明瓦里斯公式

假設(13)式成立，則

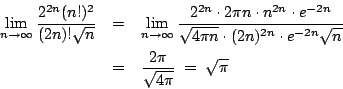
$\begin{eqnarray*} \lim_{n\rightarrow\infty}\frac{2^{2n}(n!)^2}{(2n)!\sqrt{n}} &... ...\sqrt{n}} \\ & = & \frac{2\pi}{\sqrt{4\pi}} \; = \; \sqrt{\pi} \end{eqnarray*}$

所以(18)式成立。

習題：求極限值 $\lim_{n \rightarrow \infty}\frac{\sqrt[n]{n!}}{n}$ 。

(三)由瓦里斯公式證明史特林公式

假設(18)式成立。令

$\begin{displaymath}a_n=\frac{n!}{\sqrt{n} n^ne^{-n}}\end{displaymath}$

於是

$\begin{eqnarray*} n! &=& a_n\cdot\sqrt{n}\cdot n^n\cdot e^{-n} \\ (2n)! &=& a_{2n}\cdot(2n)^{2n} \cdot e^{-2n} \end{eqnarray*}$

代入(18)式並且化簡得

$\begin{displaymath}\lim_{n\rightarrow\infty}\frac{a_n^2}{a_{2n} \cdot \sqrt{2}} = \sqrt{\pi} \eqno{(19)} \end{displaymath}$

另一方面，我們可以證明：數列 (a_n) 是遞減的且有下界。因此，考慮比值

$\begin{displaymath}\frac{a_n}{a_{n+1}}=\frac{1}{e}(1+\frac{1}{n})^{n+\frac{1}{2}}\end{displaymath}$

我們要證明 $\frac{a_n}{a_{n+1}}>1$ 。顯然下列各式都是等價的：

$\begin{displaymath}\frac{1}{e}(1+\frac{1}{n})^{n+\frac{1}{2}}>1 \eqno{(20)}\end{displaymath}$

$\begin{displaymath}\Leftrightarrow e<(1+\frac{1}{n})^{n+\frac{1}{2}}\end{displaymath}$

$\begin{displaymath}\Leftrightarrow \frac{1}{n+\frac{1}{2}}<\ln(n+1)-\ln n\end{displaymath}$

$\begin{displaymath}\Leftrightarrow \frac{1}{n+\frac{1}{2}} < \int_n^{n+1}\frac{1}{x}dx \eqno{(21)}\end{displaymath}$

今因 $y=\frac{1}{x}$ 為一個凸函數 (convex function)，並且圖二陰影梯形的面積恰為 $\frac{1}{n+\frac{1}{2}}$ ，所以(21)式成立，從而(20)式成立。這就證明了 (a_n) 是遞減數列。

由實數的完備性，可令 $\lim_{n\rightarrow\infty}a_n=L$ ，代入(19)式得到

$\begin{displaymath}\frac{L^2}{L\sqrt{2}}=\sqrt{\pi}\end{displaymath}$

從而， $L=\sqrt{2\pi}$ 。因此，史特林公式得證。

　1│2│3│4│5│6│7　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：李渭天

最後修改日期：2/17/2002