我們從最簡單情況切入,抓住形式本質,再飛躍到一般情形:
-
- (a)一維平行多面體的體積就是線段的長度:
- (b)二維平行多面體的體積就是平行四邊形的面積:
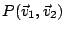 的體積
=由 的體積
=由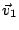 與 與 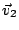 所決定的平行四邊形的面積: 所決定的平行四邊形的面積:
從表面形式上看起來,(22)與(23)兩式似乎沒有相通的地方。
但是,只要我們引入矩陣的記號與演算,將向量看作是矩陣的特例,
並且允許向量元之矩陣,那麼(24)與(25)兩式可以改寫成一致的形式:
令
則
其中
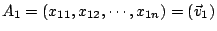 看作是
1 x 1 型向量元矩陣,而 看作是
1 x 1 型向量元矩陣,而
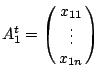 表示 A1 的轉置矩陣。其次,
表示 A1 的轉置矩陣。其次,
其中 A2 為 1 x 2 型之向量元矩陣。
由這兩個例子,我們猜測:
其中
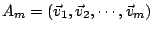 為1 x m型向量元矩陣。
為1 x m型向量元矩陣。
這個猜測成立嗎?如何證明?
首先,我們要問,什麼是m維平行多面體的體積?我們採用歸納定義法:
-
- (i)由一個非零向量
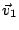 所決定的一維平行多面體之體積定義為
所決定的一維平行多面體之體積定義為
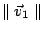 ; ;
- (ii)
假設
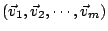 為m個獨立向量並且對於k < m,k維平行體的體積已有定義。令
為m個獨立向量並且對於k < m,k維平行體的體積已有定義。令
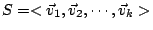 表示由
表示由
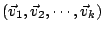 所張成的線性子空間,再令
所張成的線性子空間,再令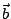 表示 表示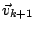 投影至S的分向量並且
投影至S的分向量並且
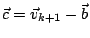 ,
於是 ,
於是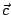 垂直於S(見圖十一)。我們定義: 垂直於S(見圖十一)。我們定義:
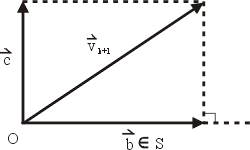
圖十一
|
注意到,如果
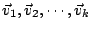 為線性相依,
則 為線性相依,
則
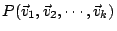 的體積為 0。
換言之, 的體積為 0。
換言之,
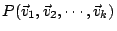 的體積是指其 m 維體積。 的體積是指其 m 維體積。
下面我們證明(28)式。首先,我們觀察到:
-
- 補題:
設
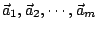 為
為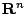 中m個向量( 中m個向量(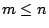 ),令矩陣 ),令矩陣
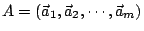 且 且
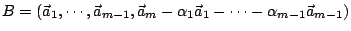 ,
其中 ,
其中
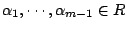 表純量,則 表純量,則
這個補題只不過是行列式的基本操作之結論,將一行(或列)乘以一個係數加到另一行
(或列),行列式的值保持不變。
- 定理六:
設
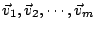
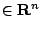 為 m 個獨立向量,則 m 維平行多面體: 為 m 個獨立向量,則 m 維平行多面體:
其中
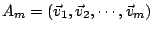
證明:利用 Gram-Schmidt 直交化手法與數學歸納法。
-
- (i)
當 m=1,2 時,(28)式化成(24)與(25)兩式,這是成立的。
- (ii)
假設 m=k>2 時,(28)式成立。對於
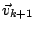 ,
如圖十一之直交化分解 ,
如圖十一之直交化分解 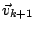 = =
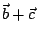 ,其中 ,其中
並且
垂直於
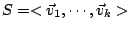 。 。
令矩陣
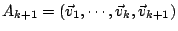 且
且
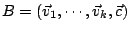 則得
則得
由歸納假設與補題知
所以m=k+1時,(28)式也成立。
對於任何 m 個向量
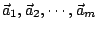 ,
令矩陣 ,
令矩陣
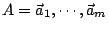 ,則 Gram 行列式 ,則 Gram 行列式
代表由
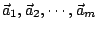 所決定的平行多面體的體積平方,因此,下面的推論是顯然的: 所決定的平行多面體的體積平方,因此,下面的推論是顯然的:
推論一:
-
- (i)
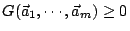
- (ii)
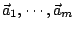 線性獨立 線性獨立
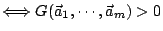
推論二:(Hadamard 行列式不等式)
-
- (i)
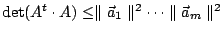
- (ii)
如果 m=n,則
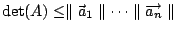
推論三:設
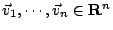 且 且
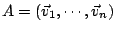 所決定的n維平行多面體的體積為
所決定的n維平行多面體的體積為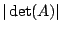 。
換言之, 。
換言之, 代表n維平行多面體的有號體積。 代表n維平行多面體的有號體積。
現在我們可以將三維歐氏空間的畢氏定理(定理三)
推廣到 n 維歐氏空間。結論很容易猜測到:一個 m 維平行多面體的體積平方,等於它投影到各個 m 維坐標空間的體積平方和。這同時含納了定理二與定理三。設
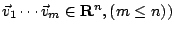 。
考慮矩陣 。
考慮矩陣
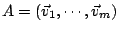 ,
這可以看成 n x m 型矩陣。如果 ,
這可以看成 n x m 型矩陣。如果
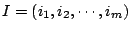 滿足 滿足
則稱 I 為從
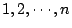 中取出 m 元遞昇指標。
令 AI 表示從矩陣 A 中取出 中取出 m 元遞昇指標。
令 AI 表示從矩陣 A 中取出
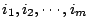 列 (rows) 所成的 n x m 型子矩陣。 列 (rows) 所成的 n x m 型子矩陣。
-
- 定理七(n 維歐氏空間的畢氏定理):
設
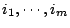 為 Rn 中的任何 m 個向量,
則 為 Rn 中的任何 m 個向量,
則
其中 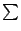 表示對 表示對
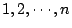 的所有 m 元遞昇指標求和,因此總共有 Cmn 項。 的所有 m 元遞昇指標求和,因此總共有 Cmn 項。
證明:假設
令
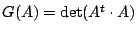 ,且 ,且
![$F(A)=\sum_{[I]} [\det (A_I)]^2$](img145.gif) 。
我們要證明: 。
我們要證明:
對所有 n x m 型矩陣 A 皆成立。我們分成五個步驟:
- (i)
當 m=1 或 m=n 時,(32)式成立:
若 m=1,則
若 m=n,則求和只有一項而已,並且有
![$G(A)=[\det (A)]^2=F(A)$](img148.gif)
- (ii)
若
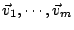 為直交 (orthogonal),則 為直交 (orthogonal),則
- (iii)
由行列式的性質知,A 的兩行互換或一行乘以一個常數加到另一行,
並不影響 F 或 G 的值。
- (iv)
經過 Gram-Schmidt 直交化手法與(iii)之操作,
可以將 A 的各行向量變成直交並且呈下形
其中
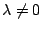 或 或 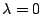 ,這樣並不影響 F 或 G 的值。 ,這樣並不影響 F 或 G 的值。
- (v)
現在對空間的維數 n 進行歸納法證明:
當 n=1 時,則 m=1,由(i)證畢。
當n=2時,則m=1或m=2,仍然由(ii)證畢。
假設對於 A 的列數比 n 少的情形 F(A)=G(A)。
令 A 為 n x m 型矩陣,由(i)知,只需考慮 1<m<n 就好了。
由(iv)知,可設 A 如下形
其中
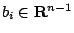 皆為直交,因為 A 的每一行向量在 Rn 中已直交。令 皆為直交,因為 A 的每一行向量在 Rn 中已直交。令
由(ii)知
其次計算 G(A)。將求和式按 im 分成兩部分
令
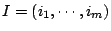 為遞昇的m元指標。
如果im<n,則AI=BI,於是 為遞昇的m元指標。
如果im<n,則AI=BI,於是
如果im=n,則
所以
由歸納法假設知
因此F(A)=G(A)
|