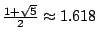黃金分割比 (第 2 頁)

　1│2│3│4　

黃金分割比（第 2 頁）

黃敏晃;方述誠

首頁 | 搜尋

．原載於科學月刊第一卷第四期
．作者當時任教於台大數學系
‧對外搜尋關鍵字

黃金分割比 (Golden section)

$\frac{1+\sqrt{5}}{2} \approx 1.618$ 這個數是很有趣的，早在古希臘時期，希臘人就給它取了個特殊名稱「黃金分割比」。種種跡象顯示，在古希臘之前，古埃及人早已發現這個神秘的數字，他們在歷史上最偉大的工程之一，金字塔的建築設計上，便大量的用到這個數值。

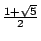被倫敦的大英博物館所珍藏，早於古希臘文明數百年的阿米斯文獻 (Papyrus of Ahmes) 中，就有西元前4700年，建築於蓋瑟 (Gizeh) 地方的大金字塔的詳細說明。該文獻中提到，在這座金字塔的構造上便用到「神聖比數」(sacred ratio)。近代的測量指出，該金字塔的斜邊長，與底層的中央到底邊長度的比值，恰好就是 $\frac{1+\sqrt{5}}{2}$ （測量只精準到小數位後第 3 位，其值為 1.618）。

如此巧妙的黃金分割比，定義作抽象的極限，似乎很不配合埃及與古希臘傳統的風格。讓我們還是尊重古老的傳統，用古典的方法來定義黃金分割比吧：在圖 1 中，長為 x+y 的線段，分成長為 x 與 y 的兩段。如果全長與較長的一段的比，及較長與較短兩段的比相等，其比值就是（設x>y）

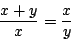$\begin{displaymath} \frac{x+y}{x} = \frac{x}{y} \end{displaymath}$

(3)

把此式乘出來得 x² - xy - y² =0 ,再以 y 除以等好兩邊得

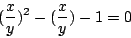$\begin{displaymath} (\frac{x}{y})^2 - (\frac{x}{y}) -1 = 0 \end{displaymath}$

(4)

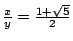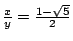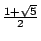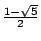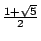把(4)式解出來得 $\frac{x}{y} = \frac{1+\sqrt{5}}{2}$ 或 $\frac{x}{y} = \frac{1-\sqrt{5}}{2}$ 。這兩個數就是(1)式中出現的兩個數了，其中 $\frac{1+\sqrt{5}}{2}$ 是正根， $\frac{1-\sqrt{5}}{2}$ 是負根，我們要的是幾何中的比值，即正根 $\frac{1+\sqrt{5}}{2}$ ，所以黃金分割比,就是這個數值。

這裡有一點值得一提的有趣的性質就是：黃金分割比是唯一與其倒數相差為一的正數，即黃金分割比減去 1，就得其倒數：

$\begin{displaymath} \frac{1+\sqrt{5}}{2} -1 = \frac{2}{1+\sqrt{5}} \end{displaymath}$

這個性質不難由(3)是直接證明得到

$\begin{displaymath} \frac{x+y}{x} = \frac{x}{y} \Longrightarrow 1+ \frac{y}{x} = \frac{x}{y} \end{displaymath}$

當然，你也無妨用有理根式的方法，得到這個關係。

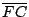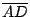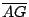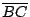讀者也許會問，給定一個線段，如何把它分割成黃金分割比呢？下列是古希臘人的方法，先做出一個黃金矩形，即其長與寬的比，恰好為黃金分割比；先取一的邊長為 1 的正方形，並連結一組組對邊的中點 E 與 F，把正方形對分為一半，再以 F 為圓心，長 $\overline{FC}$ 為半徑圓弧，交 $\overline{AD}$ 的延長線於 G 點，過 G 作 $\overline{AG}$ 的垂線，交 $\overline{BC}$ 的延長線於H。

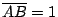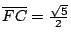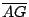
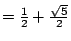
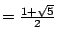此時得到的矩形 ABHG 就是黃金矩形了，因為 $\overline{AB}=1$ ，而 $\overline{FC} = \frac{\sqrt{5}}{2}$ （利用畢氏定理），所以 $\overline{AG}$ $= \frac{1}{2} + \frac{\sqrt{5}}{2}$ $= \frac{1+\sqrt{5}}{2}$ ，有了黃金矩形後，任何學過基本幾何作圖的人，都會把一段線分成黃金分割比了。

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：康明軒 ∕ 繪圖：簡立欣

最後修改日期：5/2/2002