| |
我們感興趣的問題是關於 Jensen 不等式(6)式或(7)式之幾何意義與物理意義,首先介紹質量中心:
假設平面上有 n 個點且它們皆有相同之質量,其位置向量為
 , ,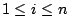 ,則質量中心之位置向量為 ,則質量中心之位置向量為
或
這意思是從 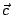 點到各點之向量彼此互相抵消。 點到各點之向量彼此互相抵消。
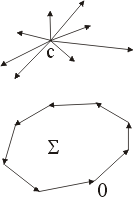
圖三
|
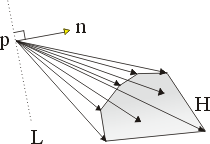
我們可以這麼想像:在每一點
 為一釘有木樁而後用一條橡皮筋連接各點 為一釘有木樁而後用一條橡皮筋連接各點
 。則如此可形成一多邊形 H(陰影區域)而這就是 。則如此可形成一多邊形 H(陰影區域)而這就是
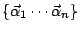 的「凸包」(convex hull)。 的「凸包」(convex hull)。
圖四
|
質量中心(9)式告訴我們的就是
這點可由圖形直觀而得。通過任意一點 P,P 在該集合之外部,我們可劃一直線 L 使得 H 及其所圍區域完全落在 L 之一邊。當然這些向量不可能互相抵消,因為它們在法向量  上均有正的分量。 上均有正的分量。
註:上面所談的這個概念其實就是泛函分析中 Banach Separation 定理之一雛形。
有了這個預備工作之後,我們回到原來的點:

圖五
|
令
K = {(x,f(x))} 為函數 f 之圖形 (graph),同時我們也連接兩端點 (x1,f(x1)),(xn,f(xn)),則由質量中心為
必定落在陰影區域 H 之內部,即
這就是(7)式,其意義為:質量中心 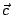 必定在圖形 K 之上方。而通過 (x1,f(x1)),(xn,f(xn)) 兩點之弦方程式為 必定在圖形 K 之上方。而通過 (x1,f(x1)),(xn,f(xn)) 兩點之弦方程式為
由圖形亦知
而且對所有
![$x \in I=[x_1,x_n]$](img34.gif) 下式成立 下式成立
這個不等式我們可視為比較定理(Comparison 定理)最簡單的形式,而這在微分方程理論中扮演著舉足輕重的角色。比較(7)與(12)式,各等式要成立其充分必要條件為質量中心 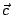 落在圖形 K 上,即 落在圖形 K 上,即
這相當於
如果將 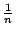 視為 xi 之機率分配(一致分配),則 Jensen 不等式(7),也可以用機率的角度來看 視為 xi 之機率分配(一致分配),則 Jensen 不等式(7),也可以用機率的角度來看
E 為期望值。
對於較一般的(6)式其意義仍是一樣的,即視 x1,…,xn 為 n 個點但其質量分別為 pi 而
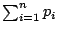 為其總質量,故有 為其總質量,故有
若視
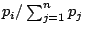 為點 xi 之機率分配,則上式可以期望值之形式表達出來,其形式與(15)式同。 為點 xi 之機率分配,則上式可以期望值之形式表達出來,其形式與(15)式同。
若仔細推敲,可知我們前面這些推導的過程中對維數 (dimension) 之依賴並不深,因此我們可自然地推廣至 n 維空間。例如設 z=f(x,y) 為一向上凹之曲面,則(7)式可推廣為
或用向量之形式
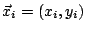
另一個方向的推廣則是想像粒子數目增加至無窮多個
 ,如此我們便可以從離散型過渡到連續型,表記如下: ,如此我們便可以從離散型過渡到連續型,表記如下:
這就是我們在數學上,尤其是分析學思想的過程而需要克服的問題──「收斂性」,即無窮級數或積分是否有意義(即是否收斂)。
在區間 [a,b] 我們可以取分割點
由(6)式知
將上式表為 Riemann 和之形式
再取極限
 ,我們就有積分形式的 Jensen 不等式。 ,我們就有積分形式的 Jensen 不等式。
-
- 定理(Jensen 不等式一)
- 若 p 滿足
 ,且 f 為一凸函數,則 ,且 f 為一凸函數,則
更一般情形則將區間 [a,b] 代換為任意可測集合 A (
![$[a,b] \rightarrow A$](img54.gif) ) )
- 定理(Jensen 不等式二)
-
讀者若有機率或測度 (measure) 之概念,則可將 p 視為一密度函數,故有
- 定理(Jensen 不等式三)
-
作個簡單的習題,其實就是例題 1 之推廣
- 例題 2:
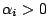 , , 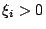 , ,
 ,試證 ,試證
|
|
|