凸函數、Jensen 不等式與 Legendre 變換 (第 4 頁)

　1│2│3│4│5　

凸函數、Jensen 不等式與 Legendre 變換（第 4 頁）

林琦焜

首頁 | 搜尋

．原載於數學傳播第十九卷第四期
．作者當時任教於成大數學系
‧對外搜尋關鍵字

四、Legendre 變換

關於 Jensen 不等式之證明，最簡單直接的方法就是用支撐線 (supporting line) 之概念，而這方法在 F. Riesz 寫給 Hardy 的信中（1930年）就曾提過關於幾何－算術平均不等式的證明，就是利用底下之不等式

$\begin{displaymath} \log t\leq t-1, \quad t>0 \eqno{(24)} \end{displaymath}$

這就是支撐線 (supportingline) 之概念。

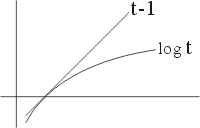
圖六

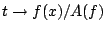若 f 為區間 (0,1) 上的一個正的且可積函數，則由(24)式知（ $t \rightarrow f(x)/A(f)$ ）

$\begin{displaymath} \log \frac{f(x)}{A(f)} \leq \frac{f(x)}{A(f)} - 1 \end{displaymath}$

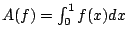其中 $A(f)=\int_0^1 f(x)dx$ 為 f 之算數平均，將上式積分一次得

$\begin{displaymath} \int_0^1\log\frac{f(x)}{A(f)}dx\leq\int_0^1\frac{f(x)}{A(f)}dx-1=0 \end{displaymath}$

由對數函數之性質知

$\begin{displaymath} \int_0^1\log f(x)dx\leq\log A(f)=\log\int_0^1f(x)dx \end{displaymath}$

或者表為

$\begin{displaymath} \begin{array}[t]{lcl} {\displaystyle \exp \big( \int_0^1 \lo... ...\fontseries{m}\selectfont \char 204})} \end{array} \eqno{(25)} \end{displaymath}$

仿此精神我們證明 Jensen 不等式

圖七

由圖形知 y=f(r)+m(x-r),m=f'(r) 為凸函數 f(x) 之支撐線 (supporting line)，即

$\begin{displaymath} f(r)+m(x-r) \leq f(x) \eqno{(26)} \end{displaymath}$

現在取 r 為質量中心

$\begin{displaymath} r=\frac{\int_A p\varphi dx}{\int_A pdx} \eqno{(27)} \end{displaymath}$

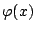而 x 則取為 $\varphi(x)$ ，則(26)式成為

$\begin{displaymath} f(r)+m(\varphi(x)-r)\leq f(\varphi(x)) \end{displaymath}$

兩邊同時乘 p 並積分得

$\begin{displaymath} f(r)\int_Apdx+m(\int_Ap\varphi dx-r\int_Apdx) \leq \int_Af(\varphi)pdx \end{displaymath}$

但由 r 之選法知

$\begin{displaymath} \int_Ap\varphi dx-r\int_Apdx=0 \end{displaymath}$

故得

$\begin{displaymath} f(r)\int_Apdx\leq\int_Af(\varphi)pdx \end{displaymath}$

這就是 Jensen 不等式。

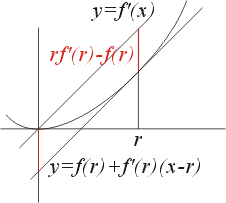
在尚未作進一步論述之前，我們不禁要對 F. Riesz 的想法獻上我們的敬意。所謂的「好數學」便是以簡單的方法來解決困難的問題，而不是學了很深的數學然後再說 "Trivial" 簡單、容易。這基本土是對數學的無知。另外一門好的數學就是其本身有「將來性」，而非解完一個問題便壽終正寢。我們要特別強調的是 Riesz 所提支撐線的概念，實際上就是 Legendre 變換之化身。不失一般性可設函數上通過原點，f(0)=0 因此通過 (r,f(r)) 之切線方程式（即支撐線）為

$\begin{displaymath} y = f'(r)(x-r)+f(r) = xf'(x)-[rf'(x)-f(r)] \eqno{(28)} \end{displaymath}$

這式子告訴我們 (f'(r),f(r)-rf'(r)) 唯一決定點 (r,f(r)) 即這兩者之間可定義某種變換關係，而這就是我們要談的 Legendre 變換。在還沒有正式談 Legendre 變換之前，我們先看看(28)式之幾何意義。

圖八

首先將切線平移為通過原點斜率為 f'(r) 之直線

$\begin{displaymath} y=f'(r)x \eqno{(29)} \end{displaymath}$

因此 [rf'(r)-f(r)] 為直線 y=f'(r)x 之 y 截距，由圖形可知其實

$\begin{displaymath} rf'(r)-f(r)=\max_x(f'(r)x-f(x)) \eqno{(30)} \end{displaymath}$

即直線 y=f'(r)x 與曲線 y=f(x) 相割後垂直距離最寬者，而這就是 Legendre 變換。記為

$\begin{displaymath} f^*(p)=xp-f(x), \quad p=f'(x) \eqno{(31)} \end{displaymath}$

直接由(31)式，即 Legendre 變換之定義可得的就是 Young's 不等式

$\begin{displaymath} xy \leq f(x) + f^*(y) \eqno{(32)} \end{displaymath}$

一般我們所熟知的形式為（利用 Jensen 不等式）

$\begin{displaymath} \begin{eqalign} xy &= \exp(\log xy) \\ &= \exp(\frac{1}{p}... ...uad (\frac{1}{p}+\frac{1}{q}=1, p>1) \end{eqalign} \eqno{(33)} \end{displaymath}$

有時候我們可略作變化

$\begin{displaymath} x \rightarrow \epsilon^{\frac{1}{p}}x \; , \quad y \rightarrow \epsilon^{-\frac{1}{p}}y \end{displaymath}$

則(33)式可改寫為

$\begin{displaymath} xy \leq \epsilon \frac{x^p}{p} + \epsilon^{-\frac{q}{p}} \frac{y^q}{q} \eqno{(34)} \end{displaymath}$

這個技巧在分析尤其是偏微分方程中是常用的。上面這些探討主要是告訴讀者 Legendre 變換之本質是支撐線 (supporting line) 而實際上就是 Young's 不等式的另一形式。除此之外，支撐線的概念也提供我們重新定義凸函數之方法：

定義： f 為一定義在區間 [a,b] 之一連續函數，若對任意的點 $\xi\in[a,b]$ 皆存在一相應之值 $\lambda=\lambda(\xi)$ ，滿足下式

$\begin{displaymath} f(\xi)+\lambda(x-\xi)\leq f(x)\quad \forall x \in[a,b] \eqno{(35)} \end{displaymath}$

則稱 f 為一凸函數。

這個定義可由 Taylor 展開式來看。f 在 ξ 點之 Taylor 展開式為

$\begin{displaymath} f(x)=f(\xi)+f'(\xi)(x-\xi)+f''(r)(x-\xi)^2 \eqno{(36)} \end{displaymath}$

若 f 為一凸函數，則 f''>0 故有

$\begin{displaymath} f(\xi)+f'(\xi)(x-\xi) \leq f(x) \end{displaymath}$

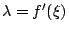因此通常(35)式中之 λ 是取 $\lambda=f'(\xi)$ 。

　1│2│3│4│5　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：黃信元 ∕ 繪圖：張琇惠、簡立欣

最後修改日期：4/26/2002