談 Stirling 公式 (第 3 頁)

　1│2│3│4　

談 Stirling 公式（第 3 頁）

蔡聰明

首頁 | 搜尋

．原載於數學傳播第十七卷第二期
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

丙、Stirling 公式的證明

定理1：（Stirling 公式，1730年）

$\begin{displaymath}\lim_{n \rightarrow \infty} \frac{n!}{\sqrt{2 \pi n}n^ne^{-n}} = 1\end{displaymath}$

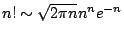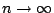記成 $n! \sim \sqrt{2 \pi n}n^ne^{-n}$ ，當 $n \rightarrow \infty$ 。

證明：

$\begin{eqnarray*} \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 226} } u_n &=& \frac{n!}{n^ne^{-n} \sqrt{n}} \\ \end{eqnarray*}$

得

$\begin{eqnarray*} n!&=&u_nn^ne^{-n} \sqrt{n} \\ (2n)!&=&u_{2n}(2n)^{2n}e^{-2n} \sqrt{2n} \end{eqnarray*}$

代入 Wallis 公式並且化簡得

$\begin{displaymath}\lim_{n \rightarrow \infty} \frac{u_n^2}{u_{2n} \sqrt{2}} = \sqrt{ \pi }\end{displaymath}$

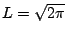再由 $\lim_{n \rightarrow \infty} u_n = L$ 得 $\frac{L^2}{L \sqrt{2} } = \sqrt{\pi }$ ，從而 $L = \sqrt{2 \pi }$ ，證畢。

Stirling 公式涉及兩個神奇的常數 π 與 e 這是其美妙的所在。物理學家 R. Feynman 每當遇到一個含有 π 的公式時，總是要問：「圓在哪裡？」(Where is the circle?) 此地我們很容易回答 π 來自 Wallis 對圓的求積公式。

利用同樣的方法我們可以證明下面深刻的結果：

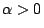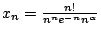定理2：設 $\alpha > 0$ ，且 $x_n = \frac{n!}{n^ne^{-n}n^{ \alpha }}$ ，則

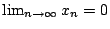: (i) 當 $\alpha > \frac{1}{2}$ 時，(x_n) 為遞減數列且 $\lim_{n \rightarrow \infty} x_n = 0$ 。
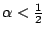: (ii) 當 $\alpha < \frac{1}{2}$ 時，(x_n) 終究遞增且 $\lim_{n \rightarrow \infty} x_n = \infty$ 。

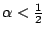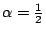換言之，當 $\alpha > \frac{1}{2}$ 時， $n^ne^{-n}n^{ \alpha}$ 高估了 n!；當 $\alpha < \frac{1}{2}$ 時， $n^ne^{-n}n^{ \alpha}$ 低估了 n!。 $\alpha = \frac{1}{2}$ 恰是分水嶺的 Stirling 公式。

證明：考慮相比

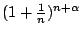$\begin{displaymath}\frac{x_n}{x_{n+1}} = \frac{(1 + \frac{1}{n})^{n + \alpha}}{e}\end{displaymath}$

我們來比較 $(1 + \frac{1}{n})^{n + \alpha}$ 與 e 之大小，我們改比較它們的對數：

$\begin{displaymath} \ln (1 + \frac{1}{n})^{n + \alpha} = (n + \alpha ) \ln ( \fr... ...ontfamily{cwM2}\fontseries{m}\selectfont \char 68} } \ln e = 1 \end{displaymath}$

由級數展開公式

$\begin{displaymath} \ln (\frac{1 + x}{1 - x} ) = 2 ( \frac{x}{1} + \frac{x^3}{3} + \frac{x^5}{5} + \cdots ), \mid x \mid <1 \end{displaymath}$

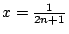令 $x = \frac{1}{2n + 1}$ ，則 $\frac{1+x}{1-x} = \frac{n + 1}{n}$ 當 $\alpha > \frac{1}{2}$ 時，於是

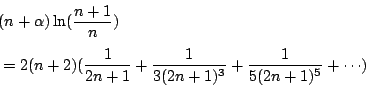$\begin{displaymath} \begin{eqalign} \lefteqn{ (n + \alpha ) \ln (\frac{n+1}{n}) ... ...frac{1}{3(2n+1)^3} + \frac{1}{5(2n+1)^5} +\cdots) \end{eqalign}\end{displaymath}$

(12)

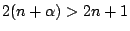(i)當 $\alpha > \frac{1}{2}$ 時， $2(n + \alpha) > 2n+1$ ，故由(12)式易知

$\begin{displaymath} (n+ \alpha) \ln (\frac{n+1}{n}) > 1 \end{displaymath}$

亦即

$\begin{displaymath}(1 + \frac{1}{n} )^{n+ \alpha} > e\end{displaymath}$

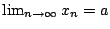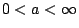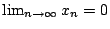因此 (x_n) 遞減，於是 $\lim_{n \rightarrow \infty} x_n = a$ 存在且 $0 \leq a< \infty$ 。如果 $0<a< \infty$ ，由 Wallis 公式會得到一個矛盾。只好 a=0，亦即 $\lim_{n \rightarrow \infty} x_n = 0$ 。

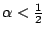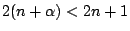(ii)當 $\alpha < \frac{1}{2}$ 時， $2(n+ \alpha) < 2n+1$ 。將(12)式中的5, 7, 9, ……皆改為 3，得到估計式

$\begin{eqnarray*} &&(n+ \alpha ) \ln (\frac{n+1}{n} )\\ &<&(2n+ \alpha )( \frac... ...\ &=& \frac{(2n+2 \alpha)(12n^2 + 12n +1)}{(2n+1)(12n^2 + 12n)} \end{eqnarray*}$

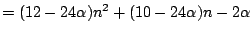分母 =24n³+36n²+12n，分子 $=24n^3+(24+24 \alpha)n^2+(2+24 \alpha )n+2 \alpha$ ，分母－分子 $=(12-24 \alpha)n^2+(10-24 \alpha )n -2 \alpha$ 。

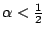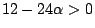今因 $\alpha < \frac{1}{2}$ ，故 $12-24 \alpha >0$ 。從而只要 n 夠大，則分母大於分子。換言之，只要 n 夠大，

$\begin{displaymath}(n+ \alpha) \ln (\frac{n+1}{n} ) <1\end{displaymath}$

亦即

$\begin{displaymath}(1 + \frac{1}{n} )^{n+ \alpha} < e\end{displaymath}$

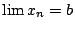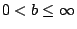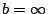於是 (x_n) 終究會遞增，故 $\lim x_n = b$ 存在且 $0<b \leq \infty$ ，同樣由 Wallis 公式會得到一個矛盾。只好 $b=\infty$ ，即 $\lim_{n \rightarrow \infty} x_n = \infty$ 。

推論：

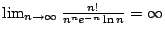
: (i) $\lim_{n \rightarrow \infty} \frac{n!}{n^n e^{-n} \ln n} = \infty$
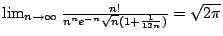
: (ii) $\lim_{n \rightarrow \infty} \frac{n!}{n^n e^{-n} \sqrt{n} (1+ \frac{1}{12n} )} = \sqrt{2 \pi}$

將上述追尋 n! 的歷程圖解如下：

n!

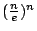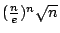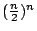$( \frac{n}{e} )^n$ $(\frac{n}{e})^n n^{\alpha}$ $(\frac{n}{e})^n \sqrt{n}$ $(\frac{n}{e})^n n^{\alpha}$ $(\frac{n}{e})^nn$ $( \frac{n}{2} )^n$ nⁿ

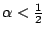$\alpha < \frac{1}{2}$ $\alpha > \frac{1}{2}$

(3) (7) (5) (6) (4) (2) (1)

低估高估

經過這麼辛苦的試誤、計算過程，終於得到美麗的 Stirling 公式，這是令人欣喜的事。唯有經過這樣的辛苦，我們對這個公式才真正有感覺 (feeling)，甚至有感情。數學公式不再是冰冷的，而是可親的。

如果將做數學比喻為登一座高山，那麼現代人大多是利用現代化的交通工具直接登到山頂（相當於直接給出公式、定理），然後就指看剛才的登山路徑（即給出邏輯證明），接著是欣賞風景（應用公式來解一些問題）。但是我們要指明，如果沒有經歷一步一步登山的流汗，沒有親自感受花草的芳香與泥土的味道，甚至嚐到偶爾的迷路，即使到了山頂也不容易領會美景的。

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：簡立欣 ∕ 校對：簡立欣 ∕ 繪圖：張琇惠

最後修改日期：4/26/2002