| |
- 例題6.1
設 t 為任意的實數,則
- 證:
將 f(t)=et 展開成 Taylor 級數具形式(2),特別我們取 n = 2, a=0 則
(注意
(f(n)(0)=1)
因為
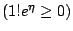
- 例題6.2
設 x 為 >0 的實數,求證函數
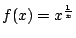 ,在 x=e 時有極大值。 ,在 x=e 時有極大值。
- 證:
至少有兩種證明方式,一種是先取對數,然後微分,使此導函數為 0 的點就是原函數取值的點,即
微分得
上式的零點是當 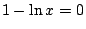 即 x=e 時,但還要進一步驗證 x=e 時 f(x) 的確取得極大值(而不是極小值!),這時嚴格的講要檢驗第二次導函數在 x=e 的值,所以並不是很清析的。 即 x=e 時,但還要進一步驗證 x=e 時 f(x) 的確取得極大值(而不是極小值!),這時嚴格的講要檢驗第二次導函數在 x=e 的值,所以並不是很清析的。
第二種證明是我們下面要提的,主要的是利用例題1。
在例題6.1中,令
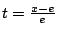 從而 從而
化簡得
兩邊開 x 次得
故易見 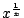 在 x=e 時有極大值。 在 x=e 時有極大值。
- 例題6.3
設 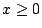 則 則
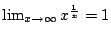
- 證:
此結果一般可用洛比脫法則來證明,但我們在此介紹利用 Taylor 級數定理不但可以證明此結果,且可對此收斂的速度有個度量。
首先設 1>a>0,則對任何 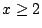 ,下式成立 ,下式成立
此可將 (1+a)2 視為 a 的函數,利用泰勒級數(2)的形式可得
其中
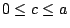 。因為 。因為 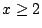 故由上式可得 故由上式可得
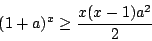 |
(10) |
設 x>1 則由
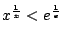 得 得
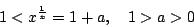 |
(11) |
從而
(1+a)x = x
由上式及式(10)兩式得
解此不等式便有
代入式(11)得
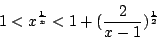 |
(12) |
即
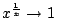 的速率至少和 的速率至少和
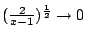 的速率相當。 的速率相當。
下面我們介紹一個基本且重要的不等式。
- 輔理1
設 |x|<1,則對任何實數 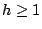 或 h<0 或 h<0
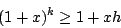 |
(13) |
- 證:
取 f(x)=(1+x)k,則
f'(x)=h(1+x)h-1,
f''(x)=h(h-1)(1+x)h-2 引用定理2可得
(因上式右邊最後一項恆為正!)。
由輔理1可得一串在高等數學分析中常用到的一些重要不等式。
- 定理6
設 y 為任意正實數,α 為實數,則
- 證:
我們只證式(14)。對式(15)的證明是完全一樣的。
令 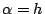 及 1+x=y 則 y>0 故由輔理1得 及 1+x=y 則 y>0 故由輔理1得
或
不等式:當 |x|<1 及
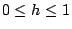 時即;式(14)得證。至於式(15)可由(讀者可仿輔理1之證法求得) 時即;式(14)得證。至於式(15)可由(讀者可仿輔理1之證法求得)
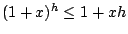 。 。
及仿式(14)的證明得到。
- 定理7
對任意兩正實數 x1 , x2 及實數 α,
- 證:
在定理6,(14)及(15)兩式中,令
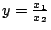 代入立即可得(16)及(17)。 代入立即可得(16)及(17)。
上面的一個推廣定理如下:
- 定理8
設
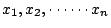 為 n 個正數, 為 n 個正數,
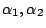 , ,
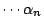 亦為 n 個正實數且 亦為 n 個正實數且
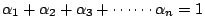 則 則
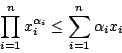 |
(18) |
- 證:
用數學歸納法,現由定理7知(18)在 n=2 時成立。假設式(18)對 n=k 時成立,我們將證 n=k+1 時亦成立。
首先不妨設在
 ,k+1 個數中, ,k+1 個數中,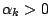 , ,
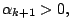 (否則就不必證明了!) (否則就不必證明了!)
令
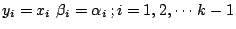
及
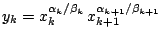
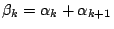
則有
由歸納法假設得知
即原式對 n=k+1 亦成立,由歸納法原理知式(18)對所有的 n 皆成立,定理8由此得證。
在定理8中若令
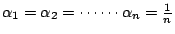 ,立即可得下面有名及常用的一些系理。 ,立即可得下面有名及常用的一些系理。
- 系理1(算數與幾何的平均定理)
設
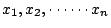 為 n 個 為 n 個 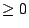 的實數,則 的實數,則
- 系理2
設 a , b 為兩正數, p,q 為不等於 0, 1 且滿足
的兩實數,則
- 證:
這是定理7的另一種形式而已。
設 p, q 為滿足
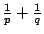 的兩正實數,令 的兩正實數,令
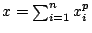 , ,
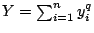 , ,
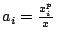 , ,
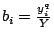 , ,
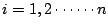
逐次將 ai 及 bi 代入(19)式中相加終於可得。
- 系理3
赫爾得 (Hölder) 不等式,若 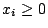 , , 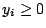 , ,
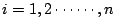
p>1, q>1 且
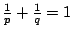 , 則 , 則
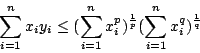 |
(21) |
- 證:
讀者不妨試討論一下以上的一些不等式,其等號在什麼情形下才成立。
利用系理3,又可導致下面一結果。
- 系理4
明可士基 (Minkowski) 不等式,設
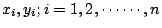 皆為非負的實數,p>1,則 皆為非負的實數,p>1,則
![\begin{displaymath}[\, \sum^n_{i=1} (x_i+y_i)^p \,]^{\frac{1}{p}}
\leq (\sum^n_{i=1} x_i^p)^{\frac{1}{p}}
+ (\sum^n_{i=1} y_i^p)^{\frac{1}{p}}
\end{displaymath}](img162.gif) |
(22) |
(若 p<1 則上不等式反向!)
- 證:
由
將上式右邊兩項分別應用系理3及
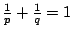 ,即 ,即
上兩式相加得
上式兩邊除以
![$[\sum^n_{i=1}(x_i+y_i)^p]^{\frac{1}{q}}$](img166.gif) 及利用 及利用
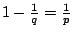 就得到(16)式。 就得到(16)式。
讀者不難證明當 0<p<1 時不等式(22)的不等號反向。由此只取兩項其他項為0,可得下面不等式:
又由上面不等式可推演得
一個似乎極明顯的事實是若
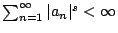 ,則可想見對 n>s 時 ,則可想見對 n>s 時
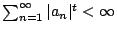 。這是因為 。這是因為
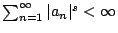 收斂。 收斂。
其表示當 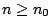 是充分大的正整數時,|an|s < 1,於是 是充分大的正整數時,|an|s < 1,於是 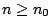 時
|an|t < |an|s,由此立即可證得 時
|an|t < |an|s,由此立即可證得
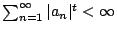 的事實。 的事實。
下面是剛剛提及的結果的推廣。
- 定理9(Jensen不等式):
設 p>0,則
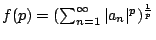 為 p 為一漸減函數。即若 q>p 則 f(p) > f(q)。 為 p 為一漸減函數。即若 q>p 則 f(p) > f(q)。
- 證:
設 q>p,令
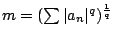 ,則 ,則
所以
因此
兩邊乘以 m 得
讀者如果熟習了以上的一些不等式,就無形中掌握了研究高深理論分析的有力工具。
|
|
|