| |
在分析上一個函數 f(x) 的導函數是指下列形式
當
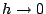 時極限存在。 時極限存在。
我們可以說若一個函數 f 具有導函數,則上式當 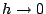 時趨向於 f'(x)。但另一方面,若我們把 h=0 代入上式分子及分母中,則得 時趨向於 f'(x)。但另一方面,若我們把 h=0 代入上式分子及分母中,則得
的不定型式。
而這也是若不加思索說「一個商式的極限為其分子及分母極限之比值」所得的結果。
這個關鍵點是我們忽略了,在這規則中能成立的先決條件是分母之極限值要不為0才行。
同樣的是
當 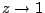 時極限值為-8,但我們若直認說「兩式差的極限,為各式極限的差」,上式就導至 時極限值為-8,但我們若直認說「兩式差的極限,為各式極限的差」,上式就導至 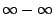 的不定型。另外常碰到的不定型有 的不定型。另外常碰到的不定型有 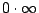 , ,
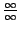 , , 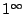 , , 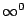 , 00 等。
我們現就討論如何利用泰勒展開式處理這些所謂的「不定型」的技巧。 , 00 等。
我們現就討論如何利用泰勒展開式處理這些所謂的「不定型」的技巧。
最簡單的情形是下面的一個結果:
- 定理4:
設 f(x) 及 g(x) 在 x=a 的泰勒展開式分別為
其中 ai, bi 等皆為常數,分別與 f 在 a 的各階導數值及 g 在 a 的各階導數值有關則
- 證:
這是因為當 h 很小時
另見定理由此得證。
- 例4.1
試證
因為 f(x)=ex-1-x 在點 a=0 的泰勒展開式為
及 g(h)=h+h3
由上定理,立即得所求的結果。
- 例4.2
試求
 ; e為自然對數的底 ; e為自然對數的底
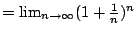 , n 為正整數。 , n 為正整數。
- 解:
設
我們先證
(注意它屬 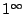 的不定型) 的不定型)
則對 G(x) 就形成
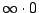 的不定型。 的不定型。
我們通常把一個函數f(x)在無窮遠點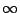 的動態作 的動態作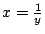 的變數變換後,討論新的函數在0點的舉止。我們現令 的變數變換後,討論新的函數在0點的舉止。我們現令
由 e 的定義為
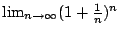 ;n為正整數。我們有 ;n為正整數。我們有
現我們要證:只要 y 趨向於0,則 F(y) 的極限值為e,即
我們將計算 F(y)-e 及 F'(0)。為此我們考慮在 |y|<1 時
由上式可知 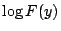 在 |y|<1 為 y 的一連續可微分的函數。 在 |y|<1 為 y 的一連續可微分的函數。
因而
也是一連續且可微分的函數。
現因
所以
現我們求
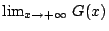 之值。 之值。
對式(9)的兩邊作微分得
(上式右邊是逐項微分的結果,要了解這個過程的合法性是需要較高深的分析理論,我們不在此介紹,讀者有興趣可翻查一般的高等微積分書必可得到滿意的解說)
由是令 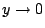 得 得
於是
從而
|
|
|