泰勒級數及其一些應用 (第 3 頁)

　1│2│3│4│5│6　

泰勒級數及其一些應用（第 3 頁）

楊重駿

首頁 | 搜尋

．原載於數學傳播第十卷第四期
．作者當時任職於美國海軍實驗室
‧對外搜尋關鍵字

3.泰勒級數或展開式

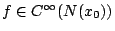設 f 在點 x₀ 的某一鄰域 N(x₀) 中為有定義的，且在 N(x₀)，f 具有任何階的導函數（以 $f\in C^{\infty}(N(x_0))$ 表之）則我們可形成一特殊形式的冪級數：

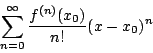$\begin{displaymath} && \sum^{\infty}_{n=0} \frac{f^{(n)}(x_0)}{n!} (x-x_0)^n \end{displaymath}$

(4)

則我們稱上式為 f 在點 x₀ 的泰勒展開式。以

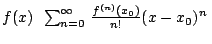$f(x) \sum^{\infty}_{n=0} \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n$ 表之

我們自然會問 (i)級數(4)除了在點 x=x₀ 外是否為收斂？ (ii)若級數(4)在點收斂，是否收斂于 f(x)？對此兩問題的答案，一般情形下為否定的。

例3.1 設

$\begin{displaymath}f(x)=\left\{ \begin{array}{lr}e^{-\frac{1}{x^2}}&x\neq0 0&x=0 \end{array}\right.\end{displaymath}$

則對任何 n，f⁽ⁿ⁾(0) 存在且皆為 0，故若取 x₀=0，則 f 在 x=0 的泰勒級數恆為 0，故除了與 f 在點 x=0 重合外，其它處與 f(x) 皆不吻合。

由泰勒公式知，若 $f\in C^{\infty} [a,b]$ （表示 f 在 [a,b] 中具有任何階的導函數），及若 $x_0\in[a,b]$ 則

$\begin{displaymath} f(x)=\sum^{n-1}_{k=0} \frac{f^{(k)}(x_0)}{k!} (x-x_0)^k + \frac{f^{(n)}(x_1)}{n!} (x-x_0)^n \end{displaymath}$

其中 x₁ 為介於點 x 與 x₀ 之間的一點，所以由上式可知泰勒級數在點 x 收斂且收斂于 f(x) 的主要條件是

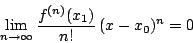$\begin{displaymath} \lim_{n\rightarrow \infty} \frac{f^{(n)}(x_1)}{n!}\,(x-x_0)^n &=& 0 \end{displaymath}$

(5)

但上面的條件涉及點 x₁（與 n 有關）。故如果我們能提供 |f⁽ⁿ⁾(x₁)| 對任何 x₁ 的值具有某個上限，使得條件(5)滿足，就可確保 f 的泰勒級數收斂于 f(x)。下面的定理就顯得很明白了。

定理3：
設 $f\in C^{\infty} [a,b]$ 及 $x_0\in[a,b],$ 若在點 x₀ 的一鄰域 N(x₀) 及存在一常數 M 使得 $\vert f^{(n)}(x)\vert\leq M ,\forall x\in N(x_0)\bigcap[a,b],n$ 為任一正整數，則對任何 $x\in N(x_0)\bigcap[a,b]$

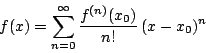$\begin{displaymath} f(x) &=& \sum^{\infty}_{n=0}\frac{f^{(n)}(x_0)}{n!}\,(x-x_0)^n \end{displaymath}$

(6)

注意：由式(6)可得下面一不等式：

$\begin{displaymath} \vert f(x)-\sum^n_{k=0} \frac{f^{(k)}(x_0)}{k!} (x-x_0)^k\vert &\leq& \frac{M(b-a)^{n+1}}{(n+1)!} \end{displaymath}$

(7)

這在數值分析上多項式逼近估計是有用的。

例3.2：

$\begin{displaymath}f(x)=\sin x \; x\in[-\pi,\pi],\end{displaymath}$

（x 表弧度）

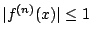則因為 $\vert f^{(n)}(x)\vert\leq1$ 及 f⁽²ⁿ⁾(0)=0, f^(2n-1)(0)=(-1)^n-1;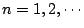 $n=1,2,\cdots$
所以

$\begin{displaymath}f(x)=\sum^{\infty}_{n=0}\frac{(-1)^{k-1}x^{2k-1}}{(2k-1)!}\end{displaymath}$

即

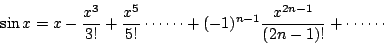$\begin{displaymath} \sin x &=& x-\frac{x^3}{3!}+\frac{x^5}{5!} \cdots\cdots + (-1)^{n-1}\frac{x^{2n-1}}{(2n-1)!} + \cdots\cdots \end{displaymath}$

(8)

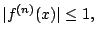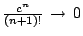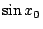這時由於 $\vert f^{(n)}(x)\vert\leq1,$ 及對任一固定的正數c, $\frac{c^n}{(n+1)!}\,\rightarrow\,0$ , 因此對一事先要求的精確度（如要求精確到小數點7位），我們總可得到一相應的正整數 m（與精確度有關）使得對任一 x₀，只要在式(8)中取前面 m 項多項式 p_m(x)，計算 p_m(x₀) 就是合精確度下的 $\sin x_0$ 的近似值。三角函數值表及一些特種函數值表就可這樣造出來了。

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：洪瑛 ∕ 校對：簡立欣 ∕ 繪圖：張琇惠

最後修改日期：4/26/2002