相異代表系古今談

　1│2│3│4　

首頁 | 搜尋

．原載於數學傳播第十卷第一期

相異代表系古今談

張鎮華

1.起源：何氏定理
2.第二把鑰匙：擬陣理論
3.電腦帶來的衝擊：匈牙利算法
4.幾個發展方向

是前生注定姻緣莫錯過
願天下有情人終成眷屬如果月下老人是數學家......

1.起源：何氏定理

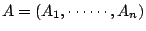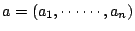相異代表系 (systems of distinct representatives，簡稱 SDR) 是1930年代的問題，我們可以把它解釋為委員會選派代表的問題，也可以將它看成月下老人牽紅線的問題。為了簡單，我們先用集合的說法描述：給定集合族， $A=(A_1,\cdots\cdots,A_n)$ ，希望在每一集合 A_i 中選出一個元素 a_i，使得 a_i, $\cdots\cdots$ ,a_n 是相異的 n 個元素；這時我們稱 $a=(a_1,\cdots\cdots,a_n)$ 是 A 的一個相異代表系。

在委員會選派代表的問題中，將集合 A_i 視為第 i 個委員會的成員集，但是每個人都可能在好幾個不同的委員會裏頭，問題就是要在每個委員會裡找到一位代表，但是同一人不能代表一個以上的委員會。在婚姻問題裏，A_i 可以看成是第 i 個女孩可能託付終身的白馬王子集，月老的任務是要將所有女孩許配給一位白馬王子，但二女不可同配一夫。

為了更瞭解問題所在，讓我們看看下面三個例子。

: 例 1： A₁ = { a,b,c } , A₂ = { c,d } , A₃ = { b,d } , A₄ = { c,d }。對這個系統，恰有兩組不同的相異代表系，就是 (a,c,b,d) 和 (a,d,b,c)。
: 例 2： A₁ = { a } , A₂ = { b } , A₃ = { a , b} , A₄ = { c,d,e,f,g,h }。這個集合族無解，因為 a 必須代表 A₁，b 代表 A₂，因此 A₃ 就找不到代表。
: 例 3： A₁ = { 3 , 4 } , A₂ = { 3 , 7 , 9 } , A₃ = { 2 , 3 } , A₄ = { 6 , 11 , 12} , A₅ = { 4 , 6 , 8} , A₆ = { 2 , 6 , 9} , A₇ = { 3 , 4 , 8 } , A₈ = { 3 , 5 , 10 , 13 }, A₉ ={ 2 , 3 , 7 , 9 } , A₁₀ = { 2 , 8 , 9 }。對於這個集合族，並不是一眼可以看出答案是什麼，在不知道好辦法的情況下，它可能浪費我們一個小時，用蠻力的方法去嘗試各種可能，最後終於得到答案了：不存在一個相異代表系。為了要讓大家信服，我們並不需要將這一小時的演算重來一次，一個簡易的方法可能是這樣的，將 A₁,A₂,A₃,A₄,A₅,A₆,A₇,A₈,A₉,A₁₀ 這 8 個集合聯集，得到 {2,3,4,6,7,8,9} 只含 7 個元素，所以不可能找到一個相異代表系。

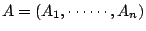例 3 的論證實在是這個問題的一個關鍵，它告訴我們，如果 $A=(A_1,\cdots\cdots,A_n)$ 在一個相異代表系，隨便拿出 k 個集合 A_i₁, $\cdots\cdots$ ,A_{i_k} 來，其聯集最少有k個元素；換言之，要說A沒有相異代表系，只要找出k個集合，其聯集的基數小於k即可。令人驚訝的是，這個必要條件同時也是充份條件，這就是著名的何菲力定理 (Philip Hall's Theorem )，我們將用和數學歸納法相等的最小原理來證明它。

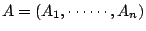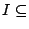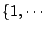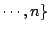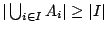何氏定理： $A=(A_1,\cdots\cdots,A_n)$ 存在一個相異代表系的充分條件是對所有 $I\subseteq$ $\{1,\cdots$ $\cdots,n\}$ 恒有 $\vert\bigcup_{i\in I}A_i\vert\geq\vert I\vert$ 。

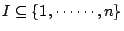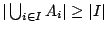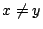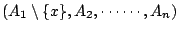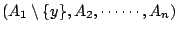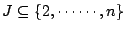證明：必要條件的證明已如上所述，現證條件為充分。如果對所有 $I\subseteq \{1, \cdots\cdots, n\}$ 恒有 $\vert\bigcup_{i\in I}A_i\vert\geq\vert I\vert$ ，我們可以假設 A 是滿足這個條件的最小集合族，也就是，從任何一個 A_i 中去掉任一元素所得的新集合族不再滿足上述條件。首先要證明的是，所有A_i恰含一元素。否則假設A₁含有x及y但 $x\neq y$ ，則 $(A_1\setminus \{x\},A_2,\cdots\cdots,A_n)$ 和 $(A_1\setminus \{y\},A_2,\cdots\cdots,A_n)$ 都不滿足上述條件，因此存在足碼集 I, $J\subseteq\{2,\cdots\cdots,n\}$ 使得

$\begin{displaymath} \vert X\vert\leq\vert I\vert \mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 47}}\vert Y\vert\leq\vert J\vert \end{displaymath}$

其中

$\begin{eqnarray*} X &=& (\bigcup_{i\in I}A_i)\bigcup(A_1\setminus\{x\}), \\ Y &=& (\bigcup_{i\in J}A_i)\bigcup(A_1\setminus\{y\}) \end{eqnarray*}$

所以

$\begin{eqnarray*} \vert I\vert+\vert J\vert & \geq & \vert X\vert+\vert Y\vert \... ...\vert+\vert I\bigcap J\vert \\ &=& 1+\vert I\vert+\vert J\vert \end{eqnarray*}$

得到矛盾,所以每一個集合 A_i={a_i} 恰含一元素,但因為何氏定理的條件, 所以這些 a₁, $\cdots\cdots$ ,a_n 都不相同,因此就得到一個相異代表系 (a₁, $\cdots\cdots$ ,a_n)。

何氏定理有許多有趣的應用,例如它可以用來得到下面兩個定理的簡潔證明。

斯伯納定理(Sperner's Theorem): 集合E恰含n個元素,F是E的子集合族,其元素兩兩互相不包含，則F最多只有( $\frac{n}{[\frac{n}{2}]}$ )個元素。

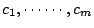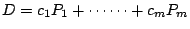伯考夫-馮紐曼定理(Birkhoff-von Neumann Theorem): 一個雙重隨機矩陣 (doubly stochastic matrix) 是一 n x n 的非負實數矩陣，其任一行或列的和恰為1；若其元素均為0或1，則稱為排列矩陣 (permutation matrix)，因為它恰和一個 $\{1,2,\cdots\cdots,n\}$ 上的排列相對應。定理是說，若D是雙重隨機矩陣，則存在排列矩陣 $P_1,\cdots\cdots,P_m$ 及和為1的正實數 $c_1,\cdots\cdots,c_m$ 使得 $D=c_1P_1+\cdots\cdots+c_mP_m$ 。例如

$\begin{displaymath} \begin{eqalign} \lefteqn{ \left[ \begin{array}{cccc} 0.3 &0.... ...&0&0 \\ 0&0&1&0 \\ 1&0&0&0 \end{array}\right] \end{eqalign}\end{displaymath}$

從文獻上考據，何氏定理始於1935年，事實上在1931年柯尼哥 (D. Konig) 和亞哥法利 (E. Egervary) 就曾以不同的語言（即 (0,1) 矩陣或二分圖網），證明到相同的結果；尤有甚者冕哥 (Meger) 在1927年時，研究圖網的連通性，就有一些更一般化的定理，將前三者的結果視為特殊情況。何氏定理重要的貢獻是，這樣描述的定理，開啟了一些緊閉的窗扉，通向往日鮮為人知的大道。從1930年代到1950年代之間是相異代表系的起步時期,其中雷多 (Rado) 的貢獻頗多；一直到1960年代，這套理論和擬陣理論(matroid theory)相結合，才大展異彩。

對外搜尋關鍵字：
．von Neumann

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：林君怡 ∕ 校對：黃怡碧 ∕ 繪圖：簡立欣

最後修改日期：4/26/2002