相異代表系古今談 (第 3 頁)

　1│2│3│4　

相異代表系古今談（第 3 頁）

張鎮華

首頁 | 搜尋

．原載於數學傳播第十卷第一期
‧對外搜尋關鍵字

3.電腦帶來的衝擊：匈牙利算法

在1960年代的熱潮裏，另外一個異軍突起的是電腦。電腦的興起完成人類快速計算的美夢，許多以前人們不敢奢望的問題，再度被拿出來借助電腦無怨言的快速計算順利完成。但是電腦的快速也有其一定的極限，於是一門新興的學問-算法(Algorithm)-廣泛的研究。

舉例來說，站在理論的觀點，何氏定理無疑的是一個極漂亮的定理，但從實用的立場來看，它似乎毫無發揮的餘地。隨便給n個集合，若想用何氏定理驗證是否存在一個相異代表系，就必須把 2ⁿ-1 種不同的 k 個集合拿出來，看它們聯集是否存在最少k個元素。一方面，當n大時，2ⁿ 大得不可思議，再者即使驗證出的答案是肯定的，何氏定理也沒告訴我們那一組是相異代表系，為此，我們需要一個有效的算法。

把相異代表系轉換成二分圖網 (bipartite graph) 上求對集 (matching) 的問題是一種方便的語言。一般而言，一個圖網 (graph) 包含有限個頂點 (vertices) 以及一些聯接兩個頂點的邊 (edges)，如圖1 的 A₁,A₂,A₃,A₄,a,b,c,d 是頂點， (A₁,a),(A₁,b), $\cdots\cdots$ 是邊，但圖上 (A₁,c) 和 (A₃,b) 兩邊另外相交的點並不算做頂點，換言之，聯接某兩頂點的邊其實只表示這兩點是「有關係」或「相鄰」而已，至於用直線或曲線表示，實無區別。

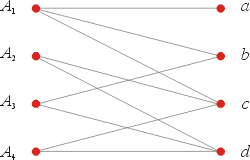
圖1

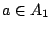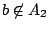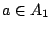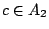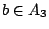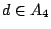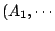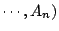圖1的圖網就是所謂的二分圖網，因為頂點可以分為兩部分，其中任一部分內的任二頂點不相鄰。這個二分圖網事實上也就是例1的集族的圖網表示法； $a\in A_1$ 所以 (A₁,a) 是一條邊， $b \not \in A_2$ 所以 (A₂,b) 不是一條邊。 (A₁,A₂,A₃,A₄)是一組相異代表(a,b,c,d),在圖網上相當於(A₁,a), (A₂,c),(A₃,b),(A₄,d)四邊,分別表示 $a\in A_1$ , $c\in A_2$ , $b\in A_3$ , $d\in A_4$ ;這四邊中的任兩邊沒有共同頂點, 因為我們找不同集合的相異代表,圖2中粗線表示這四邊。像這種兩兩不含共同頂點的邊所組成的集合稱為對集(matching)。所以求 $(A_1,\cdots$ $\cdots,A_n)$ 的一組相異代表, 相當於在它所對應的二分圖網中找一個有n邊的對集。

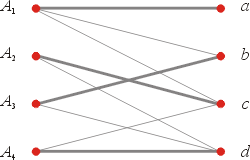
圖2

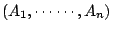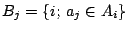用二分圖網表示集合族 $(A_1,\cdots\cdots,A_n)$ 的另一好處是可以看出集合A_i和元素a_j的對稱性, 如果對每一元素a_j,定義集合 $B_j=\{i;\:a_j\in A_i\}$ , (A₁, $\cdots\cdots$ ,A_n) 和 (B₁, $\cdots\cdots$ ,B_m) 所對應出來的二分圖網實際上是同一圖網(可能頂點左右相反,名稱各異)。在婚姻問題中,這表示男女平等。

隨便給一集合族 (A₁, $\cdots\cdots$ ,A_n) 不一定存在相異代表系, 所以在它的二分圖網中,也不見得能找到一個n邊的對集。一般來說, 我們有興趣的是,隨便給一個二分圖網,求一個具有最多邊的對集, 有名的匈牙利方法(Hungarian method)就是解決這問題的好算法。

給定一個二分圖網G=(X,Y,E),其中X和Y合成所有頂點,E是邊集, 任一邊的一端點在X內,另一端點在Y內。另給定G中的一個對集M, 如圖3(a)是一個例子,粗線代表對集M。

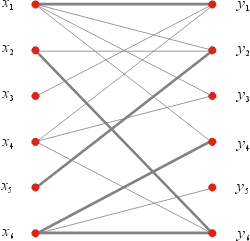
圖3(a)

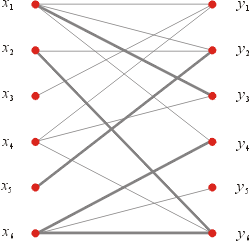
圖3(b)

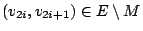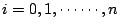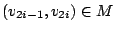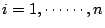G 的一條M-可擴張路徑 (M-augmenting path) 是含有 2n+1 個頂點的一條路徑 (v₀,v₁,v₂, $\cdots\cdots$ , v_2n,v_2n+1)，其中 $(v_{2i},v_{2i+1})\in E\setminus M$ , $i=0,1,\cdots\cdots,n$ , 但是 $(v_{2i-1},v_{2i})\in M$ , $i=1,\cdots\cdots,n$ 並且 v₀ 和 v_2n+1 是M-暴露頂點(M-exposed vertices)，也就是 v₀ 和 v_2n+1 不是 M 內任何邊的端點。例如圖3(a)中 (x₃,y₁,x₁,y₃) 是一條 M-可擴張路徑。

找到一條M-可擴張路徑 P 的好處是，如果將M在P的邊去掉，換上P 中不在M的邊，將造成一個新對集M^*，其邊數比原來M的邊數增加1。圖3(b)就是用上述M-可擴張路徑做出來為M^*。

: 貝爾齊定理(Berge Theorem)：任一圖網（不一定是二分圖網）中的對集M是最大對集的充分條件是不存在 M-可擴張路徑。

匈牙利方法簡單的說就是從二分圖網G=(X,Y,E)的任意對集M(例如空集合) 開始,有系統的尋找M-可擴張路徑，若找到就得到一個更大的對集，再繼續一直到不存在M-可擴張路徑為止。尋找M-可擴張路徑的方法如下述。

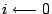: (甲) $i\longleftarrow 0$ ;列出所有M-暴露頂點當作第i層。
: (乙) 當i是偶數時:依次列出和第i層頂點相鄰的頂點當作第i+1層, 但被列出過的頂點不再重複;若第i+1層沒有頂點則停止, 表示沒有M-可擴張路徑。當i是奇數時: 若有某個第i層的頂點是M-暴露頂點, 表示找到一條M-可擴張路徑; 否則將第i層每一頂點所聯接的一條M邊找出來, 另一端點當作第i+1層頂點。
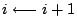: (丙) $i\longleftarrow i+1$ ;回到(乙)重做。

以圖3(a)為例,可以得到下圖;其中我們賦予偶(奇)數層的頂點以正(負)號, 這是為了以後說明方便。

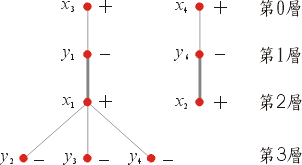
圖4

因為y₃(負號)是M-暴露頂點,所以找一條M-可擴張路徑, 就是 (y₃,x₁,y₁,x₃),這是由y₃倒返回去找到的。由這個M-可擴張路徑得到一個更大的對集,如圖3(b)所示, 再做一次得到下圖,表示不存在M-可擴張路徑,所以已經找到最大對集。

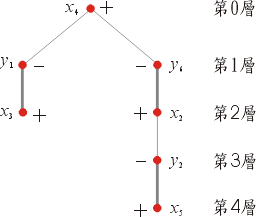
圖5

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：林君怡 ∕ 校對：黃怡碧 ∕ 繪圖：簡立欣

最後修改日期：4/26/2002