| |
設想我們再作一連串的試驗,而每次試驗所可能發生的結果定為 E1,E2,… En,…。(可能是有限也可能是無限)。
每一個結果 Ek,我們若能給定一個出現的可能性 pk(即機率),則對某一特定樣本之序列
Ej1 Ej2 … Ejn,我們知道它出現的機率是
p(Ej1 Ej2 … Ejn) =pj1
… Pjn。這個是試驗與試驗彼此互相獨立的基本精神。但在馬可夫鏈的理論中,我們的目的就是要擺脫「獨立」的這個假設,因此我們沒有辦法知道(也就是沒有辦法給定)每一個事件出現的可能性;
也就是說「pk」是不存在的。不過我們總得要知道一些東西才能討論,
所以在馬可夫鏈中我們考慮最簡單的「相關」性。在這種情況下,我們不能給任一個事件 Ej 一個機率 pj 但我們給一對事件 (Ej,Ek) 一個
機率 pjk,這個時候 pjk 的解釋是一種條件機率,就是假設在某次試驗中 Ej 已經出現,而在下一次試驗中 Ek 出現的機率。除了 pjk 之外
,我們還須要知道第一次試驗中 Ej 出現的機率 aj。有了這些資料後,一個樣本序列
Ej0 Ej1 … Ejn(也就是說第零次試驗結果是Ej0,第一次試驗是 Ej1……第 n 次試驗是 Ejn)的機率就很清楚的是
P(Ej0,Ej1,Ejn)
=aj pj0j1 pj1j2 …
pjn-1jn。
有了以上的概念後,現在讓我們用一些數學符號來表示這些數量。
在常用的術語中,用 S 來表示狀態空間,也就是一個試驗所有可能出現的狀態所成的集合。令 Xn 表示在第 n 次試驗的結果。所以 Xn 是一個隨機變數,它的取值是在狀態空間S中。
-
- 定義1:
- 一組值在 S 中的隨機變數 X0,X1,X2
 稱為馬可夫鏈。如果它滿足以下的條件: 稱為馬可夫鏈。如果它滿足以下的條件:
其中 x0, x1,…,xn+1 皆屬於 S。
(1)式的意思是說我們以 Pxy 或 P(x,y) 表示 P
(
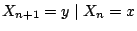 ),假設我們知道第 0 次到第 n 次的試驗結果,則第 n+1 次的試驗結果僅僅和第 n 次有關,我們舉一些例子來看:(為了簡單起見,本文只討論平穩的馬可夫鏈。也就是說(1)中的轉換機率和狀態有關但和時間無關。) ),假設我們知道第 0 次到第 n 次的試驗結果,則第 n+1 次的試驗結果僅僅和第 n 次有關,我們舉一些例子來看:(為了簡單起見,本文只討論平穩的馬可夫鏈。也就是說(1)中的轉換機率和狀態有關但和時間無關。)
- 例一:
- 設有一賭徒甲帶了現金若干去賭場賭博。如果他每贏一次則贏一元而每輸一次也輸一元,
同時贏的機率是 p(輸的機率就是 q=1-p),則 X0,X1,X2,
 顯然是一個馬可夫鏈。(Xn 表示他賭 n 次後手中所有的資金)為什麼呢?
因為僅僅需要知道 Xn 的值就足以預測 Xn+1 的值,另外 顯然是一個馬可夫鏈。(Xn 表示他賭 n 次後手中所有的資金)為什麼呢?
因為僅僅需要知道 Xn 的值就足以預測 Xn+1 的值,另外
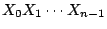 並不能幫助我們做更好的預測。在這個例子中,
並不能幫助我們做更好的預測。在這個例子中,
- 例二:(衍生鏈)
- 設想在細胞分裂中或是中子分裂的情況。第 0 代的細胞數(起始點)設為 X0,從第 n 代衍生出來的細胞個數稱為第 n+1 代,用 Xn+1 表示。
在衍生的過程中,一個細胞可能分裂成二個或保持不變,也可能消失或(死亡),若畫圖表之,這種衍生有點像樹狀圖:
〔十分抱歉,這個圖檔已遺失〕
在這個例子中,X0,X1 … 是一個馬可夫鏈。因為第 n+1 代的個數顯然是和第 n 代的個數有關,但另外再告訴我們第 0,1,… n-1 代的個數並不能幫助我們做更好的估計。
- 例三:
- 假設有無窮多個瓶子,我們標以 0,1,
 。每一個瓶子中放不同個數球,每瓶中的球都標以 B0,B1,B2, 。每一個瓶子中放不同個數球,每瓶中的球都標以 B0,B1,B2, 等(不同的球可以有相同的編號),假設我們從標以 0 的瓶中隨便抽一個球,則此球的編號是 Bj,我們再從第j個瓶中抽取一球,若此球編號是 Bk,我們再從第 k 個瓶中抽取一球,……這樣一直做下去,我們就得到一個馬可夫鏈。原因和前面幾個例子相同。事實上任一個馬可夫鏈都和這個模型等價,我們只要適當的選取每個瓶中球的個數,同時加以適當的編號,我們就可得取第一和第二個例子。 等(不同的球可以有相同的編號),假設我們從標以 0 的瓶中隨便抽一個球,則此球的編號是 Bj,我們再從第j個瓶中抽取一球,若此球編號是 Bk,我們再從第 k 個瓶中抽取一球,……這樣一直做下去,我們就得到一個馬可夫鏈。原因和前面幾個例子相同。事實上任一個馬可夫鏈都和這個模型等價,我們只要適當的選取每個瓶中球的個數,同時加以適當的編號,我們就可得取第一和第二個例子。
- 例四:
- 考慮一個基因由 n 個單位所合成的。在此 n 個單位中,每一個不是正常的就是突變的。
現在這些細胞要分裂,分裂前基因先要完全複製一次,也就是有了 2n 個單位。假設一個細胞一分為二,則此二個子細胞中的基因也是有 n 個單位,但此 n 個單位是由原來母細胞中 2n 個單位隨意挑選出來的!
若以 Xn 表示細胞分裂 n 次後某一個子細胞中突變單位的個數,則 X0,X1,
 也是一個馬可夫鏈。
讀者可以試試看把 也是一個馬可夫鏈。
讀者可以試試看把
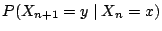 寫出來。 寫出來。
|
|
|