.原載於數學傳播第七卷第二期、第七卷第三期
.作者當時任教於美國海軍研究實驗所;美國佛羅里達大學統計系
楊重駿;楊照崑
|
|
.原載於數學傳播第七卷第二期、第七卷第三期 .作者當時任教於美國海軍研究實驗所;美國佛羅里達大學統計系 | ||
|
數論在密碼上的應用
楊重駿;楊照崑 |
|
數論,顧名思義,是一門研究數字性質的學問。一般所謂的數論,特指正整數(即自然數)的許多性質,像質數的分佈,方程式的正整數解,韓信點兵,及進位法都包括在數論裏面,我們在小學時候學的分解因數,最大公約數也是數論的一部分,可惜因為數論在日常生活中沒有什麼直接的用處,在中學數學裏很少提到數論,一般被認為是一種「純數學」,深而無用。可是「無用之用,真乃大用」,終於在一九七0年代後期,幾個電機工程師用數論的一些基本定理,製成了一種新的密碼。這種由數論所作成的密碼與以前人們所用的密碼,有著根本性質上的不同,可說是密碼史上一個空前的革新。
密碼通訊在軍事上的用途是大家都知道的,但由於交通的發達,在分秒必爭的工商業社會裏,商業上的情報也已成為商業盈利的主要依靠。譬如說,有人早幾個小時知道什麼公司有了一種新的發明,或某兩個公司計劃合作,或某地區有物價的大波動,就可以在股票上上下其手, 轉瞬之間收進大筆的財富。因此公司本身內部及公司與公司之間的通訊都希望能對外嚴守機密。但由於現在通訊無論是有線或無線都很容易被敵方竊聽,因此公司必須對情報加鎖,即所謂密碼通訊。
以往人們在軍事上所用的密碼其基本的形式在於「代換」與 「置換」。譬如說,我要發出下面一個消息給你,
「我有一個秘密對你說」
我就先把這幾個字換成數字,即一般電碼本上的代碼,假定「我」字的代碼是3314,「有」字的代碼是1432,「一」字代碼是0001,等等,則上面那句話就成了
331414320001 …
代換密碼是把 0,1,2,…,9 十個數字互換,譬如我們可以把 0 換成 2,1 換成 3,等等,若用群論的符號表示,上面的代換可寫成
這個表示法是上行為 0,1,2,…,9,而下行是他們代換成的新數字,即0 這時一個不知道這個代換規則的人看到了上面的信號,他就不能從電碼本子裏找出它的原意了。置換法在於把密碼排成一種雙方都知道的形式,如下圖 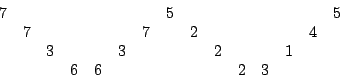
則發出的信號為755772433216623,同樣的,不知道這種特定圖案的人,很難解開原來的信息。
以代換法為例,像G這類的轉換可以有10!=3,628,800種不同的變化,假定我們可以在一分鍾內試一種代換,又假定我們的運氣中等,在試到一半時即10!/2=1,814,400時可以成功,則在不吃、不睡、不錯的情形下,我們要試3年零165天,等迷解出來的時候,仗早已打完了。但這只是最基本的密碼而已,在生死關頭,更難解的密碼必然出籠,例如在代換法中,若兩位兩位的代換(即00
因此解密碼,都不用硬試的方法去解。一般可用統計的方法根據名字(或字母)出現的頻率及發生的事件加以分析,例如在英語中,各字母出現的頻率按多少排列是
因此一個出現次數最多的符號就很可能代表 e,出現次多的符號就很可能代表a,並以此類推,但道高一尺, 魔高一丈,如果不斷地變化代換的方法,譬如說前一百個字用代換法G1, 第二個一百個字用代換法 G2,則頻率方法亦失去功效。但是魔高一丈, 惡魔又高一丈,重賞之下,天下尚沒有絕對解不開的密碼。二次大戰時, 美國密碼兼統計學家弗立得門(W.F. Friedman),在一年半的時間完全破獲了日軍的密碼。 在中途島一戰,美國海軍以劣勢的軍力,大勝日本皇家海軍 (讀過參加該戰役的日本軍官淵田美津雄及奧宮正武所著的《中途島》一書嗎?)。另外英國也幾乎在同時解開了德軍的密碼,做到了知己知彼的優勢地位(知己知彼並不一定百戰百勝,但總比不知彼要好得多。) 過去這類密碼的特質(也可以說是缺點)在於它們是關閉式的製解法,即收發雙方都必須同時知道這種密碼的構造。因此如果在一通訊系統中有一個聯絡站被間諜滲入或被敵人佔領,則密碼的機密可能全盤暴露。而現在用數論的密碼卻是公開式的 (Public-Key Cryptography),即是只有收方知道密碼的解法, 發方只需要知道做法而已,而且這種製法可以公開。因此即使發方被捕,敵人仍榨不出解密碼的機密來,其程序是這樣的:
當然把收發互換,就可以互通信息了。剛才說過這種方法最大的好處就是只有一方知道解碼的秘訣,比以前收發雙方都知道秘訣的保密性高多了,自從這類的密碼法發表之後,在美國軍事界、教育界、工商業界引起了一個蔚然大波。對大多數的數論而言則是一則以喜,一則以懼。喜的是,皇天不負苦心人,一向不容易找到飯吃的數論家突然成為許多經費充裕的軍工商界所爭取的對象。費馬、尤拉以及那些一生窮困而已作古了的數論家可以含笑九泉了。但懼的是,由於這些理論在軍事通訊上的價值,有關這方面的新發現已被視為國防機密而列為管制了。以往各國數論家無憂無慮發表論文自由交換意見的日子也許是一去不返了,前程固然似錦,往事卻是如煙,純數學最後一塊淨土也終於被實用所「污染」了。然而這次因密碼而推動大家對數論的研究,將在數學史上寫下了有趣的一頁。
這種密碼所用的數論並不深,我們可以全部介紹出來,當然在實際用的時候,數字會大得多,但在大小型電子計算機如此普遍的今日,是不會成問題的。
在我們介紹兩種主要的數論密碼之前,我們先將介紹一點數論。
|
對外搜尋關鍵字: .數論 .Public-Key Cryptography .費馬 .尤拉 .尤拉函數 .密碼學 |
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:陳文是 / 繪圖:簡立欣 | 最後修改日期:6/17/2002 |