| |
|
�G�B�]�l�B��ơB�P�l���P�O���B�שԩw�z |
�Y m,n �����ơA�B m>0�A�h�H m �� n �i�o�G��� �\ �P r�A�ϱo
�䤤 �\ �٬��ӡAr �٬��l�ơA�B 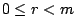 �C�Y r=0�A�h�ڭ̻� n �i�Q m �Ҿ㰣�Am �� n ���]�l�An �� m �����ơA�Y�@�ư� 1 �P�������~�L��L�]�l�A�h���ƺ٬���ơA�Ҧp 2,3,5,7,11 ���O��ơA4,6,9,12 �o���O��ơC�ڭ̩w�q n �P s �� m ���P�l�ơG �C�Y r=0�A�h�ڭ̻� n �i�Q m �Ҿ㰣�Am �� n ���]�l�An �� m �����ơA�Y�@�ư� 1 �P�������~�L��L�]�l�A�h���ƺ٬���ơA�Ҧp 2,3,5,7,11 ���O��ơA4,6,9,12 �o���O��ơC�ڭ̩w�q n �P s �� m ���P�l�ơG
�p�G n �P s �Q m ���ɦ��ۦP���l�ơC�Ҧp
���@������P�l����²��w�z�A�ڭ̧⥦�̦C�X�ӡAŪ�̫ܮe���ҥX�ӡC
- �w�z2.1
- �Y
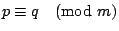 �A �A
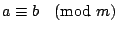 �A
�h �A
�h
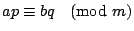 �C �C
�Y�⥿��� p,q ���̤j���]�l(����)�O 1�A�h�ڭ̺� p,q ����A�H
(p,q)=1
���ܤ��C�{�b�ڭ̭n�Ҥ@�Ӧ�����Ӥ���ƪ��@�Ӱw�z�C
- �w�z2.2
- �Y�⥿��� p,q ����A�h�i�H���G���(���@�w��) a,b�A�ϱo
ap+bq=1
- �ҩ��G
- �O A ���t�Ҧ� x=ap+bq>0�Aa,b ����Ƥ����X�A�����X��M���O�Ŷ��X�A�]�i��a=b=1,p+g>0�C�Od�������X�����̤p�̡A�Yd=1�A�h���w�z�o�ҡA�Yd>1�A�Oap+bq=d>1�A�h�������������t�@�ơC
a'p+b'q�A�h�ڭ̭Y�Hd��a'p+b'q�A�h�o
�N�J
d=ap+bq
�h�o
��r����0�A�_�hr��A�����@�p��d���ơA�P���]d���̤p�Ƭۥ٬ޡA�]r=0�Gd��A��������@�Ƥ��]�l�C�]
�Gd��p�Aq�����]�l�C��p�Aq���̤j���]�l��1�A�Gd=1�A�w�z�Ҳ��C
�o�O�@�ӷ����Ϊ��w�z�AŪ�̤]�\�n�ݡA�ڭ̦p����a�Pb��ap+bq=1�O?�@��i������۰��k�C
- �ҡG
- ���� a,b�A�ϱo 5a+9b=1�C�]
�G
1=5-4=5-(9-5)=2 x 5-9 x 1
�G
- �t2.2
- �Yw�Pm���G���誺����ƥBm>w�A�h�i���@����ƣc�ϱo
- �ҩ��G
- �ѩw�z���A�� a�Bb �G��ƨϱoaw+bm=1�A�]bm��m�����ơA�G
�O
�h�o
�]�c���i�ର0�A�G���t�o�ҡC
�̫�ڭ̭n�Ψ�@�Ӥ��e���ҩ����u�O���B�ש� (Fermat-Euler) �w�z�v�C���]���ڭ̥u�Ψ�o�өw�z����e���ҩ����S���Φ��A�ڭ̴N�u�ҩ�²�檺�����C
- �w�z2.3
- �Ym����ơAw�����@�Pm���褧��ơA�h
- �ҩ��G
- ����w�g��w��1���M�A�h�Ѧh�����w�z��
���i�}������w��1���~�A���t��m���]�l�A(m�����m!����m���i����h)�A�G
���䭼�H�t2.2����a�A�Y
�o
���w�z�Ҳ��C
- �t2.3
- �Y m ���G��� p�Bq ���n�Aw �����@�P m(�Y�P�ɻP p �P q ���褧��ơA�h
- �ҩ��G���Ωw�z���ҩ��k�o
�ѩw�z2.1�i�o
�Y
�Y
�]wp-1�Pm����A�Ѩt2.2���ҩ��i���s�b�@ a ��
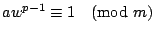 �A�W�����Ha�o �A�W�����Ha�o
�Y
���t�Ҳ��C
�ڭ��٭n�Q�Ψ�t�@��²�檺�w�z�A�ڭ̤]�b�o�`�ا⥦�ҧ��C
- �w�z2.4
- �O (a1,a2,�K,an) ���@�tn�ӥ���ƪ��ƦC�A�ú���
�S�O (x1,x2,�K,xn) ���@��0�P1�զ����ƦC�A�Y�Ҧ���xi���O0�N�O1�A�{�]a1�Aa2�A�K�Aan���w���Ax1�Ax2�A�K�Axn�������Ac���@����ơA�h��{��
�u���@�ѩεL�ѡC
- �ҩ��G
- �]����{�����G�� (x1,x2,�K,xn) �� (x1',x2',�K,xn') �h���h c ����i�o
�]
�B
�Gan���Y�ƥ���0�A�Yxn=xn'�A�]��
�P�z�i�o
����ѭ쬰�@�C���w�z�o�ҡC
�ӭn��(2.2)�O�D�`�e�����ơA�]���Y
�hxn����1�A�_�h����0�A�P�z�Y
�hxn-1����1�A�_�h����0�A�H�������A�@�U�l�N�ѥX�ӤF�C
�o�X�өw�z�N�����A�ѷs���K�X�k�F�C
|
|
|