高中解析幾何後記 (第 4 頁)

　1│2│3│4　

高中解析幾何後記（第 4 頁）

黃武雄
筆記：阮貞德

首頁 | 搜尋

．原載於數學傳播第五卷第一期
．作者當時任教於台灣大學數學系

‧註釋
‧對外搜尋關鍵字

第四節、

現在我們有了射影平面及其上的射影變換群，可以開始來答覆兩個老問題：

問題 A：（橢圓、拋物線與雙曲線的整合問題）
設若地平面（假定為平坦而無限伸展）上有一拋物線，有人站若對它拍照，會發覺照片上出現的是一個漏了上端一點的橢圓。如果地平面上畫的是雙曲線的話，假定這人站在雙曲線兩葉之間，沿雙曲線軸朝其中一葉，拍下來得到的照片會是橢圓的一部份，今反身再朝另外一葉拍照，又得橢圓的另一部份，兩部份接合一起，會發覺除漏掉黏接虛的兩點外，竟合成好端端的一個橢圓。

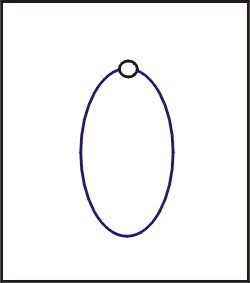
看拋物線，拍下來的照片，其上是只漏一點的橢圓。

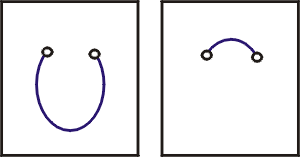
看雙曲線，朝相異兩方向各拍下來的照片，兩張合起來正好是一個漏點兩點的橢圓。

問：用射影幾何怎麼來解釋，這一巧合的現象？

現在我們來答覆這個問題，對於歐氏平面E²上的一條二次曲線（假定為非特異的情況，例如不流為兩相交直線，平行直線，甚或虛解等等）：

$\begin{displaymath}\Gamma :Ax^2+2Bxy+Cy^2+2Dx+2Ey+F=0\eqno{(1)}\end{displaymath}$

把它放到射影平面，它應變成

$\begin{displaymath}\Lambda :Ax^2+2Bxy+Cy^2+2Dxz+2Eyz+Fz^2=0\eqno{(2)}\end{displaymath}$

P² 中所決定的點集，這裡 [x,y,z] 了表示 P² 中的齊性座標。（為什麼？請回想 E²，正好是 z=1 的平面）。但(2)式在齊性座標空間中代表橢圓錐鉗頂在原點，此因適當變換座標，可將(2)式化成

$\begin{displaymath}\lambda_1\overline{x}^2+\lambda_2\overline{y}^2+\lambda_3\overline{z}^2=0\eqno{(3)}\end{displaymath}$

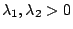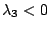其中 $\lambda_1,\lambda_2 >0$ , $\lambda_3<0$ （不然便屬特異）。而(3)式所代表的顯然是個橢圓錐（自己想想）。因此(2)式在齊性座標空間中便如下圖所示：

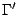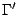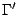注意橢圓錐Λ與z=1平面相交於 Γ，而與球面 x²+y²+z²=1相交處記為 $\Gamma '$ 。

$\begin{displaymath}\Gamma =\Lambda\bigcap E^2,\Gamma '=\Lambda\bigcap S^2,\end{displaymath}$

從 $\Gamma '$ 的位置來看Γ

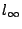(1) $\Gamma '$ 與 $l_{\infty}$ 相離時，Γ即為構圓

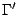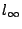(2) $\Gamma '$ 與 $l_{\infty}$ 相切時，Γ即為拋物線

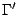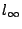(3) $\Gamma '$ 與 $l_{\infty}$ 相交時，Γ即為雙曲線

採用這種射影觀點，我們可有

定理: 在射影幾何中，橢圓，拋物線，雙曲線，事實上都無分軒輊。

解說: 因為三者都以齊性座標空間中的橢圓錐(Λ)來代表，只是橢圓錐的位置不同，才造成三種不同的情況，但利用射影變換(即齊性座標空間中的線性變換)，可將三種情況相互轉化，故以射影變換為運動群的射影幾何中，三者相互之間沒有區別。

於是我們答覆了問題 A 的拍照現象，照片上遺漏的一點(或兩點)，正是拋物線(或雙曲線)與無窮遠線 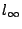$l_{\infty}$ 的切點(或兩交點)。

用這種觀點，我們也能分享計算上的好處，舉個例子:

[例] 求 x²-xy-3y²+2x-y+4=0 的漸近線。

作法一:(通常用平行直線族的求法)

以 y=mx_n+k_n 代入原式，集項得

(2-m-3m²)x_n²+(-k_n-6mk_n+2-m)x_n+(-3k_n²-k_n+4)=0

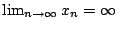兩端除以 x_n²，因 $\lim_{n\rightarrow \infty}x_n=\infty$ 故

$\begin{displaymath} 2-m-3m^2=0, \quad \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 41}} \; m=\frac{2}{3},-1, \end{displaymath}$

又僅除以 x_n²，亦得 -k-6mk+2-m=0，得 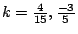$k=\frac{4}{15},\frac{-3}{5}$ ，故

$\begin{displaymath}y=\frac{2}{3}x+\frac{4}{15}\mbox{\hskip 1.2pt plus0.4pt minus... ...mily{cwM2}\fontseries{m}\selectfont \char 68}} y=-x-\frac{3}{5}\end{displaymath}$

為所求兩漸進線

作法二:(用射影幾何的觀點)
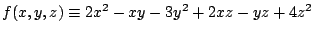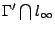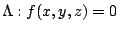設 $f(x,y,z)\equiv 2x^2-xy-3y^2+2xz-yz+4z^2$ ， [(2)式]在齊性座標空間中，兩漸近線應為分別在 $\Gamma ' \bigcap l_{\infty}$ 所含之兩交點上，與 Λ 相切的平面 π 所代表的射線直線，要求出這方程式，考慮 $\Lambda : f(x,y,z)=0$ 的法向量

$\begin{displaymath}\begin{array}{rcl} \nabla f&=&(4x-y+2z,-x-6y-z,2x-y+8z)\\ &&... ...family{cwM0}\fontseries{m}\selectfont \char 44}}\\ \end{array}\end{displaymath}$

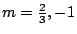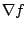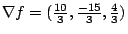設 Λ 與 Γ 的切線為 (t,mt,0):t 為實數，則 (t,mt,0) 應滿足(2)式，故 2t²-t²m-3m²t²=0 得 $m=\frac{2}{3},-1$ ，今分別代回 $\nabla f$ 中，得 $\nabla f=(\frac{10}{3},\frac{-15}{3},\frac{4}{3})$ ，(5,5,3) 故 π 為 10x-15y+4z=0 或 5x+5y+3z=0

其在 E² 上相應的直線便是(代以 z=1)

$\begin{displaymath} 10x-15y+4=0 \quad \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 67}} \quad 5x+5y+3=0 \end{displaymath}$

即

$\begin{displaymath} 2x-3y+\frac{4}{5}=0 \quad \mbox{{\fontfamily{cwM2}\fontseries{m}\selectfont \char 68}} \quad x+y+\frac{3}{5}=0 \end{displaymath}$

為所求兩漸近線。

最後我們再提一下交點問題：

問題B：在歐氏平面上，考慮一條直線（滿足一次方程）與一條拋物線（滿足二次方程），從代數著眼，如果把重數 (multiplicity) 計算在內，應有兩個交點（不管實交點或虛交點），如圖：

但事實上，會出現這種狀況

所丟失的交點掉到哪裡去？

通常交點丟失的原因，是實數系本身並非「代數完備」 (algebraically closed)。也就是解實係數的代數方程不一定總有實根，例如：求 y=x²+3 與 y=1 的公解，相當於求

x²+3=1

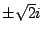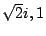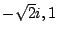的根，但它沒有實根，卻仍有虛根 $\pm\sqrt{2}i$ ，所以雖然沒有實交點，我們仍說它有虛交點：( $\sqrt{2}i,1$ ) 與 ( $-\sqrt{2}i,1$ )，這便是上圖(3)中的情況。

但(4)卻道道地地只有一個實交點，另外一個交點丟在什麼地方（顯然不會又是虛交點，因虛根總是成對存在的，不會只有一個虛交點）？現在有了射影平面，我們發覺另一實交點，事實上在無窮遠線上：

同樣，考慮直線與雙曲線：

在(6)與(8)中，所丟失掉的交點都掉在無窮遠處：

如果考慮的數系是像複數系那麼有代數完備性的數系，且又引入無窮遠點的話，那麼上述的討論可以得到完整的推廣，這便是著名的 Bezout 定理：

定理：在射影平面上，任兩條代數曲線，若次數分別為m與n（即分別可表為m次與n次方程的解），其相交交點個數如果重數與實、虛皆計算在內，必定恰好有mn個。換句話說，在複數射影平面 (complex projective plane)上，任兩代數曲線恰好有 mn 個交點，其中 m,n 分別為兩條代數曲線的次數。

於是我們明白了在射影平面上，交點並沒有丟失。在歐氏平面上找不到的東西，在射影平面中找回來了，只因射影平面是歐氏平面外加一條無窮遠線，很多歐氏平面上的缺憾，在射影平面中就彌補過來了。從代數方程式論的眼光看來，射影平面是完整得多。這就是為什麼代數幾何學都要在射影空間(尤其是複射影空間)中討論的緣故。

高中的解析幾何基本上是用代數處理幾何，是沿依上述的方向在進行的，因此我把這篇引介射影幾何的稿子稱做「高中解析幾何後記」。

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：鄧惠文 ∕ 繪圖：簡立欣

最後修改日期：6/17/2002