上頁　1│2│3│4　次頁

高中解析幾何後記 （第 3 頁）

黃武雄
筆記：阮貞德

 

首頁 | 搜尋

．原載於數學傳播第五卷第一期
．作者當時任教於台灣大學數學系

•註釋
•對外搜尋關鍵字
 
第三節、

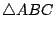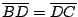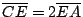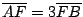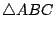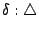用 Klein 的 Erlangen Program 的觀點來說，考慮射影幾何，就是要討論射影變換下的不變性。 這個觀點的意思，我們不妨再用個例子加以說明，今年大專聯考有個題目說「在$\triangle ABC$ 三邊 BC,CA 及 AB 上分別取點 D,E,F 使 $\overline{BD}=\overline{DC}$， $\overline{CE}=2\overline{EA}$， $\overline{AF}=3\overline{FB}$， 設三直線 AD, BE, CE 所圍成的三角形面積為 δ，而 $\triangle ABC$ 的面積為 $\triangle$，求 $\delta:\triangle$ = ?」



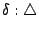如果做的時候，較座標 B=(0,0), C=(a,0), A=(b,c) 表示 A,B,C 處於一般的相關位置，計算會變得十分繁複，但若用心想想題目中所牽涉的條件只是共線三點的分比及面積間的比例，這些是不因線性變換(或進一步說，仿射變換)而變，故可以考慮特殊的情況：即 B=(0,0), C=(1,0), A=(0,1) 的情形(或為更簡化計算，考慮 B=(-1,0), C=(1,0), A=(0,1))，據此特殊情況算出來的 $\delta:\triangle$ 不因作線性變換而異，從而歸結得一般情況下的答案。

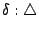這個例子說明了利用 Klein 的觀點：「 $\delta:\triangle$ 是仿射變換下的不變性」我便可節省計算上的麻煩。

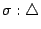今天我們要談的是射影變換，它比仿射變換更加廣義。像上述 $\sigma:\triangle$ 的問題是仿射問題，但不再是射影問題，因為在射影變換下，分比與面積比例都變掉了。

到底什麼是「射影變換」呢？把兩平面作平行光的射影：



所得的還只是仿射變換的特殊情況。（仿射變換＝線性變換＋平移，此類平行投影所相應的仿射變換，其線性變換的部份有一固有值為 1。請注意兩平面交線！）

如果更進一步，對兩平面作光源射影：



則很多性質(例如共線三點間的分比)都改變了。射影變換是一連串的平行光或光源射影的組合。注意光源射影並不能對每一點都作確定的投射，比如說圖中L線上的點經O投射出去無法在另一平面上落實，只好說L線投射到所謂的「無窮遠線」上去。

射影變換基本上便是一連串的平行光或光源射影的組合。為討論方便，若將光源移到無限遠，便得平行光射影，因此平行光射影可以當作光源射影的特別情況。但這樣射影變換要處理起來相當複雜。從十七世紀以來，Desargues, Pascal, Monge相繼做了一些工作，這些工作大體可以稱為綜合射影幾何，到了十九世紀初Carnot, Brianchon, Poncelet之後有了解析方法，處理起來才較容易，這段方法上的沿革，就像從平面綜合幾何進展到解析幾何一樣，是方法上的一大進步。今天我們為了讓討論本身較容易掌握，採取了解析方法。而解析方法的基礎便是引入座標，界說其運動群。

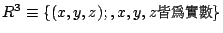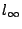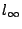把歐氏平面 E2 插到 $R^3\equiv \{(x,y,z);,x,y,z\mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \ch... ...pt plus0.2pt minus0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 98}}\}$中， 插入的方式是使 E2 成為 z=1 所代表的平面， 所謂「射影平面」事實上是在E2之外補進一些「無窮遠點」， 這些無窮遠點的全體構成一條所謂的「無窮遠線$l_{\infty}$」，換句話說， 射影平面 P2 便是 E2 再補上 $l_{\infty}$。



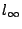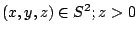但無窮遠線 $l_{\infty}$ 應補在哪裡呢？取單位球 S2，以原點 O 為心，以 1 為半徑。把光源放在 O 處，於是 P 上每一點都是球面上某點 P* 的投影，因此可暫時將 E2 上的點 P 用球面上的點 P* 來代表，這些歐氏平面的代表們正好充斥於東半球（即 ${(x,y,z)\in S^2;z>0}$）。現在情況比較明朗了，當 P 往無窮遠跑的時候，它的代表點 P* 則往子午線

\begin{displaymath}l_{\infty}^*\equiv\{(x,y,z);z=0\}\end{displaymath}

趨近，因此我們就將 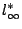$l_{\infty}^*$ 充當無窮遠線的代表。

到目前為止，我們很人工的用東半球來「代表」歐氏平面，用子午線來「代表」無窮遠線，以下我們要做兩件事：

(一) 如果在球面上要做射影幾何，把球面的東半球加上子午線當做「射影平面」，視覺上還算清楚，但計算上就很大的困難，所以我們要引入所謂的「齊性座標」，把射影平面再加改造，使計算容易進行，且保持E2原有的一些代數性質，例如E2上的一條二次曲線，放到P2上來是否仍然允當的稱它為二次曲線？

(二) 界說其上的運動群，使它仍易於拿來計算，並說明它正好是上面所說「射影變換」的全體。

對於射影平面上的點，若看 E2={(x,,y,z);z=1}的點P無法涵蓋無窮遠點，若看球面上的代表P*，雖可逼近無窮遠線，計算上卻不方便且相當程度破壞了射影平面上的代數性質。於是我們乾脆這樣做：把順著OP射出的整條直線「視為」射影平面上的「一點」!這是怪異的想法，但卻徹底解決了處理射影幾何的困難。

定義1: 設等價類 $[x,y,z]\equiv{(\lambda x,\lambda y,\lambda z);\lambda \mbox{{\fontfamily{cwM1}\... ... minus0.1pt{\fontfamily{cwM0}\fontseries{m}\selectfont \char 47}}\lambda\neq 0}$， 這裡x,y與z三實數不同時等於0，我們說這樣的[x,y,z]的全體組成射影平面P2。 以後「P2上的一點α」指的便是這樣的等價類[x,y,z]，常記成 $\alpha=\alpha[x,y,z]$。

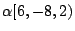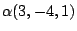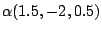注意(一): 由於等價類[x,y,z]是自由度為1(亦即有一個參數λ)的直線 (但扣除O點)，所以P2上的點雖然有三個座標x,y,z， 實際上只剩兩個自由度。注意:(6,-8,2),(3,-4,1),(1.5,-2,0.5), (-0.75,1,0.25)……等等各點， 現在都「黏」成了同一點 $\alpha[6,-8,2)$, (當然也可寫成 $\alpha (3,-4,1)$, $\alpha (1.5,-2,0.5)$……)， 而不分彼此。

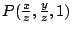注意(二)： 幾乎每一(除非z=0)等價類[x,y,z]都與E2交於一點 $P(\frac{x}{z},\frac{y}{z},1)$。因此這些等價類便相當於E2上原有的點，至於z=0的情況，[x,y,0]便代表新增補的無窮線，所以說

\begin{displaymath}E^2=\{[x,y,z];x,y,z \in R \mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 47}}z\neq 0\subset P^2\}\end{displaymath}

而

\begin{displaymath}l_{\infty}=\{[x,y,0];x,y \in R\subset P^2\}\end{displaymath}

定義2： 當一些等價類的聯集恰好是一個空間中的平面(但扣除O點)，則稱這些等價類組成P2中的一條直線，換句話說，滿足

\begin{displaymath}ax+by+cz=0 \quad (\mbox{{\fontfamily{cwM2}\fontseries{m}\sele... ...inus0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 6}})\end{displaymath}

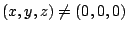的所有[x,y,z](仍要求 $(x,y,z)\neq (0,0,0)$)，稱為組成P2中的直線。

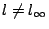注意： 設l為P2中的一條直線，且 $l\neq l_{\infty}$則l在E2上的代表點正好是滿足

\begin{displaymath}ax+by+c=0\quad (\mbox{{\fontfamily{cwM0}\fontseries{m}\select... ...nus0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 41}})\end{displaymath}

的(x,y,1)的軌跡，這與歐氏空間E2中原來所謂的直線吻合。至於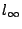$l_{\infty}$的方程式便是

\begin{displaymath} z=0 \quad (\mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont... ...s0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 245}}) \end{displaymath}

如果考慮 P2 中直線 l 在球面上的代表點全體，則它構成大圓的半弧（兩端點等價，看成同一點）



定義3： 射影平面P2上的運動群G便是以齊性座標[x,y,z]來表示射影平面上的點時,x,y,z 三變數的線性變換群，亦即

\begin{displaymath}G=\{ [x,y,z]\stackrel{f_A }\rightarrow[x',y',z'];\end{displaymath}


\begin{displaymath} \left( \begin{array}{c} x'\\ y'\\ z'\\ \end{array}\right)... ...ontfamily{cwM9}\fontseries{m}\selectfont \char 179}}(a_{ij})\} \end{displaymath}

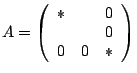注意： 當 $A= \left( \begin{array}{ccc} *&&0\\ &&0\\ 0&0&*\\ \end{array}\right)$ 時，則fA將E2映至E2，且是E2上的仿射變換群。 我們可以證明如下定理，來說明G限制在E2時便是前述的射影變換(證明當做習題)。

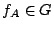定理： 對任意$f_A\in G$，

\begin{displaymath}(x,y)\rightarrow (\frac{a_{11}x+a_{12}y+a_{13}z}{a_{31}x+a_{3... ...{33}z},\frac{a_{21}x+a_{22}y+a_{23}z}{a_{31}x+a_{32}y+a_{33}z})\end{displaymath}

正是前述一連串光源射影的組合。

   

上頁　1│2│3│4　次頁

 回頁首
 
（若有指正、疑問……，可以在此 留言 或 寫信 給我們。）
EpisteMath

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有


編輯：鄧惠文 ／ 繪圖：簡立欣 最後修改日期：6/17/2002