質數 (第 4 頁)

　1│2│3│4　

質數（第 4 頁）

唐文標

首頁 | 搜尋

．原載於數學傳播第四卷第四期
．作者當時任教於英國劍橋大學
‧對外搜尋關鍵字

(四)小結

找尋質數的方法雖然尚未定案，有史以來，人類不斷的努力，相信這種努力一定會繼續下去。

1830年，H.J. Scherk 說過，只要選擇得，+或-號，

$\begin{eqnarray*} p_{2n}&=&1 \pm p_1 \pm p_2 \pm \cdots\cdots +2p_{2n-1}(n\mbox{... ...98}})\\ p_{2n+1} &=& 1 \pm p_1 \pm p_2 \pm \cdots\cdots +p_{2n} \end{eqnarray*}$

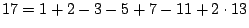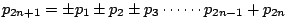
例如： p₆=1+p₁-p₂-p₃+p₄+p₅, $17=1+2-3-5+7-11+2\cdot 13$ 或可改為 $p_{2n+1}=\pm p_1 \pm p_2 \pm p_3 \cdots\cdots p_{2n-1}+p_{2n}$

例： 17=2+3-5-7+11+13。自然，這些公式對追尋新的質數並無實際好處。

千百年來，為了尋質數，人們發現不少定理，例如：

: 定理：
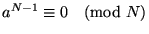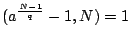如果 N-1=FC，其中 F 的質因子 q 已知，且 F>C>0，若 $a^{N-1} \equiv 0 \pmod{N}$ 且 $(a^{\frac{N-1}{q}}-1,N)=1$ ，對每一個 F 的每一個質因子 q 皆為真，則 N 是一個質數。

例如：

$\begin{displaymath} N=9,999,999,900,000,001=\frac{10^{24}+1}{10^8+1} \end{displaymath}$

$\begin{displaymath} N-1=\frac{10^{24}-10^8}{10^8+1}=10^8(10^8-1) \end{displaymath}$

令

F=10⁸,a=7

因此，

$\begin{displaymath} 7^{\frac{N-1}{10}}=8383924385890424= r \pmod{N} \end{displaymath}$

可以計算出 $[(r^2-1),N]=(7^{\frac{N-1}{5}},N)=1$

$\begin{displaymath} r^5 \equiv -1 \pmod{N} ,\quad r^{10} \equiv 7^{N-1} \equiv 1 \pmod{N} \end{displaymath}$

故 N 為質數。

有關這類的「分解因子」的問題，可以參看

R.Guy(1975):〈How to Factor a number〉. Proc. 5^th Manitoba Conference on Numer. Math. and Comput. Univ. of Mamitoba. Canada.

Lehmer:(1969):《computer technology applied to the theory of numbers》. (Studies in Number Theory )MAA(美國數學會叢書)

我們結束這篇小報告之前，介紹二個現代研究問題。看看！

(A)容易明白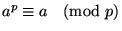， $a^p \equiv a \pmod{p}$ , 若 p 是質數的話。因此

$\begin{displaymath} 1^{p-1}+2^{p-1}+ \cdots +(p-1)^p+1 \equiv \pmod{p} \end{displaymath}$

能否用這個公式來反證「逆定理」呢？即證明此式為真時則 p 為質數呢？有人查過在 n=10¹⁰⁰⁰ 下皆為真，但證明仍毫無頭緒。

(B)有人 [參考 Jones, Sato, Wada, Wiens 的《Diophantine Representation of the set of prime numbers》, 1976, Am. Math. Monthly.] 計算出，質數集合與一個二十五次的二十六個變數的多項式所有的函數值相同：

$\begin{eqnarray*} & &(X_{11}+2)\{1 -[X_{23}X_{26}+X_8+X_{10}-X_{17}]^2 \\ &-&[(... ...12}(X_1-X_{16})+X_{20}(2X_1X_{16}-X_{16}^2-1)-X_{16}X_{13}]^2 \} \end{eqnarray*}$

你說，怎樣辦呢？

: 1.K.S.S. Namboodiripeq; 〈A note on formula for the n^th Prime〉, Monat. fur Math 75 (1971) 256-262.
: 2.L. Moser. 〈A prime Representing function〉, Math. Mag. (1950).
: 3.C. P. Willans, 〈On formula for the n^th prime Number〉, Math Maz. 48(1964). 413-5.
: 4.Sato. E. G. strauos, 〈p-adic proof of non-existence of proper prime representing algebric functions and related problems〉, J.L.MS. Ser 2.2(1970)45-8
: 5.Dudler, 〈History of a formula for primes〉, AMM 76(1969).23-8
: 6.W.H.Mills, 〈A prime retresenting function〉 BAMS 53(1947).604
: 7.Roberts, 《Elementary Number Theory》. MIT (1977)
: 8.Beiler, 《 Recreations in the Theory of Numbeis》. Dover (1966).
: 9.Sierpinski著，林聰源譯，《整數論問題》（What we know and what we don't know about primes）
: 10.李恭晴：《整數論》

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強

最後修改日期：4/26/2002