質數 (第 3 頁)

　1│2│3│4　

質數（第 3 頁）

唐文標

首頁 | 搜尋

．原載於數學傳播第四卷第四期
．作者當時任教於英國劍橋大學
‧對外搜尋關鍵字

(三)質數方程式

上節所談到的函數 $f(n)=p_1\times p_2\times\cdots\cdots\times p_n+1$ ，我們期望找到一個類似的函數，對任何變數值（一個整數），我們得到的f(n)函數值皆是質數。即是我們

對所有整數 n, f(n)= 質數, n=0,1,2,…

(A)多項式的質數方程

若這多項是 0 次的，那麼 f(n)=p 雖滿足所求，但一無用處，故可以不論。若這多項式是一次的，那麼 f(n)=an+b。要這個方程式成功，an+b 一定是一個算術級數（等差級數），例如

$\begin{displaymath}3,5,7 \leftrightarrow f_1(n)=2n+1 \quad n=1,2,3\end{displaymath}$

但當 n=4 時，f(4)=9，便不是了。較長一點的

199,409,619,829,1039, 1249,1459, 1669, 1879,2089.

都是質數，方程式為 f₂(n)=210n+199, n=0,1,2,…,9 很顯然 n=199 時一定不是質數，事實上，還不用那麼大，n=10 時 f(10)=2100+199=2299，可被11除盡。

這說明了不可能有一串都是質數的算術級數。事實上，若果 $\Phi(a)$ 代表尤拉函數，(小於aX又與a互質的正整數之個數)則數列(an+b) 中質數的個數(當小過一個數目N時)約略等於 $\frac{N}{\Phi(a)\log{N}}$ 。如上題，令 $N=10,\Phi(a)=3$ ，故約 $\frac{10}{4}=3$ 。

結論是，沒有一個像an+b樣子的函數可以包含全是質數的。也許轉來問一下，這樣形式的質數是否無窮呢？

Dirichlet（Dirichlet 定理，可在《數論導引》中第九章找到證明。）曾證明，若 $(a,b)=1, \; a,b$ 互質，則 {an+b} 有無窮多個互質如 4n+1 形式的質數有 5,13,17,29 $\cdots\cdots$ ；6n+1 有 1,7,13,19 $\cdots\cdots$ ；12n+7 有 7,19,31,43,67 $\cdots\cdots$ 但是在 (6n+3) 中只有一個 3 是質數，而在 6n+4 中沒有一個質數。一般說來，如 p 不是 a 的因子，則形如 an+b 的數列每隔 p 項便有一個為 p 除盡的數了。如上文 f(n)=210n+199，可見 11 不是 210 因子，即每隔 11 項一定有一個 11 可除盡的項了。由這條定理看來。要求長一點的連續質數數列也不太容易，目前知，如

$\begin{displaymath}f_3(n)=30030n-6887,n=1,2,\cdots\cdots,12\end{displaymath}$

含連續 12 個質數已是很長了。例如 f(x)=x²-2999x+2248541，由 1460 到 1539 的 x 值一共連結有 80 個使 f(x) 函數值是質數。一次方程式既不可能，不妨找二次方程式試試：在形式如 ax²+bx+c=f(x) 中，我們也找到不少。

$\begin{displaymath} \begin{array}{lll} f_1(n)=n^2-n+17 & -15 \leq n \leq 16 & \\... ...+21n+1 & -38\leq n \leq 17 & f_6(18)=703=19\cdot 37 \end{array}\end{displaymath}$

當然，我們可以無限的追求下去，但很顯然 ax²+bx+c 不可能永遠是質數，因如 ax₀²+bx₀+c=p，則 x_k=x₀+kp 一定得為 p 整除，也是說 {an²+bn+c} 這個數到每隔 p 項一定被 p 整除。同樣理由也可以推廣到三次多項式，如 $f(n)=x^3+x^2+17,-14 \leq n\leq10$ 。但是，類似在一次多項式中的 Dirichlet 定理，證明 an²+bn+c 形式有無限的質數存在的定理，還未存在，所以我們並不能知道上述任何一個以二次多項式所表示出來的數列中具有無限多的質數。

連最簡單的 n²+1 的形式中是否含有無限多質數我們都不知道，雖然 2,5,17,37,101 $\cdots\cdots$ 15537 $\cdots\cdots$ 等都是。目前僅知道的是，有無限個 (n²+1) 形式的數具有最多三個質數因子而已。推廣這類多項式到高次；可以參考 Halberstam and Richert 在1975年出版的《篩法》(Sieve methods, Academic Press)。

不過，所謂求一條長的質數數列是一件難事，端指我們希望找到一個多項式 f(n)，使 f(n) 能帶給我們「很多」（更好是全部都是）新的質數。即找出我們仍未知道的質數。

若僅僅為了一條長長的質數數列，那麼從已知的質數推出來，竟是一件輕而易舉之事，例如我們可以逆推之。例如要使得 f(0)=3,f(1)=5,f(2)=7,f(3)=11 則 3f(n)=n³-3n²+8n+9 便可以了。若要使得 f(0)=3, f(1)=5, f(2)=7, f(3)=11, f(4)=13, f(5)=17，則 60f(n) = 7n⁵-85n⁴ + 355n³ - 575n² + 418n + 180 才可以。換言之，若要求出一個含有 100 個已知的連續（任何已知的！）質數數列的多項式，只要依樣就可以製造出一個 101 次的多項式出來， $f(n)=a_nx^{101}+\cdots$ 只是，這些多項式一無用處。並不帶給我們任何新的質數。

我們主要目的在於找出一條能供應我們無限多的新鮮的質數的「方程式」來。上述的所有質數多項式完全不能符合這個需要，因為代入 n 值以後，我們還無法知道得出的是否為一個質數呢！（更別談它是否有無窮個如此形狀的質數了？）例如 n²+1 多項式，究竟 n=10¹⁰，是否出現質數，n=123456789 呢？這還要乞靈電腦去查呢！

(B) 多項式質數公式表

我們可以證明，不可能有一條多項式函數 f(x)，它的函數值都是質數的，即是若 $f(x) = a_kx^k + a_{k-1}x^{k-1} + \cdots + a_1x + a_0$ , $k \geq 1, a_k$ 係數皆是整數。令 x=b，不可能所有整數 b，都令 f(a) 常為一質數。

證明的方法根據另一定理：

若 $f(x) = a_kx^k + a_{k-1}x^{k-1} + \cdots + a_1x + a_0$ , $k\geq 1$ 是一整係數多項式，如果

$\begin{displaymath} b & \equiv & c \pmod{n} \end{displaymath}$

則

$\begin{displaymath} f(b) & \equiv & f(c) \pmod{n} \end{displaymath}$

因此，令 p=f(a)>2，（即 p 是多項式 f 之一值）設正整數值 J，能使

f(a+Jp) > n

但

$\begin{displaymath} a+Jp \equiv a \pmod{p} \end{displaymath}$

故使

$\begin{displaymath} f(a+Jp) \equiv f(a) \pmod{p} \end{displaymath}$

但

$\begin{displaymath} f(a) \equiv p \pmod{p} \end{displaymath}$

即 p 能整除 f(a)，因此整除 f(a+Jp)。

這就是說，不管是什麼次數的多項式，一定周期後必然會有一個合成數出現，因而有無限個合成數。

新的難題卻是，有了無限個合成數，那麼質數是否亦屬無限呢？以多項式形式出現的質數是否無限，仍屬未解難題。

我們並且知道，設 f 和 g 都是多項式，則 $\frac{f(n)}{g(n)}$ 亦不可能對所有 n 都給出一個新質數出來。

參考 M. Davis 〈Hilbert 10^th problem is unsolvable〉AMM(1973)233-269。

目前所知最大的算術級數之質數公式，是

$\begin{displaymath} f(n)=223092870n+2236133940,\quad n=0,1,2,\cdots\cdots,15 \end{displaymath}$

（見 Edgar Karst〈12 to 16 primes in arithmatic progression〉, Journal of Recreation Mathematics, (1969) 二次多項的質數公式有下列的表算。

質數公式表

f(x)公式	在100以下令f(x)成合成數的x值	總數
x²-79x+1601	80, 81, 84, 89, 96	5
x²+x+41	40,41,44,49, 56, 65, 76,81,82,84,87,89,91,96	14
2x²+29	29, 30, 32, 35, 39,44, 50, 57, 58, 61,63, 65,	25
	72,74,76, 84,87, 88, 89,91,92,94,95, 97, 99
6x²+6x+31	29, 30, 31, 34, 36,41,44, 51, 55, 59, 61, 62,	25
	64,66, 69,76,80, 84, 86. 87, 88, 92, 93, 97, 99
3x²+3x+23	22,23,27, 30, 38,43, 44,45,46,49, 51, 55, 56, 59,	28
	62,66,68, 69,70,78, 85, 87, 88, 89, 91,92,95,96

像質數公式 x²+x+41，我們能找到連續 40 個（由 0 到 39）的質數究竟還有無同樣類似公式的可能呢？即是：

問題：有沒有一條質數公式 f=x²+x+b，能使 (b-1) 個連續 x 值使 f(x) 都是質數呢？有人曾用電算機去找，結果查出如果有，則 b 值一定要超過 1,250,000,000，而且最多只有一個。看來這個問題大概解不了。

「多項式」這一類函數，既然無法辦得到所有函數值都是質數，那麼只有轉求到其他類型的函數了。

指數類型函數讓我們來研究一下指數類的函數 $f(n)=[\theta^n]$ 吧。

例如函數

$\begin{displaymath} f(n)=[(\frac{3}{2})^n] \quad [ \quad] \mbox{ {\fontfamily{cw... ...nus0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 98}} \end{displaymath}$

那麼

$\begin{eqnarray*} f(2)&=&[(\frac{3}{2})^2]=[\frac{9}{4}]=2 \\ f(3)&=&[(\frac{3}{2})^3]=[\frac{27}{8}]=3 \end{eqnarray*}$

此外，我們還有 f(4)=5,f(5)=7,f(6)=11,f(7)=17

但

$\begin{eqnarray*} f(8)&=&[(\frac{3}{2})^8]=[\frac{6561}{256}]=25 \\ f(9)&=&[(\frac{3}{2})^9]=3[\frac{19683}{512}]=38 \end{eqnarray*}$

都不是質數，而且下一個質數要到

$\begin{displaymath} f(21)=[(\frac{3}{2})^{21}]=4987 \end{displaymath}$

直到今日，還沒有人能證明，像 $f(n)=[\theta^n]$ 公式不可能永遠給我們一個新質數的，但也不知道這類公式可以無限地供應質數，換句話說，每一個由這類公式得出來的函數值，還要仔細計算查證，才能肯定是否質數。

令人驚喜的是，果有一條類似的定理，是 W.H. Mills 證明的。

: [質數函數定理]：
我們可以找到一個實數 θ，使函數 $f(n)=[\theta^{3^n}]$ 的值對所有 n=1,2, … 都是質數。

這條定理在《數論導引》有證明，主要的根據是另一條頗深的定理，在 n 和 2n 之間必有一個質數存在，（Bertrand 臆測）這裡我們引出的定理，則是根據 Riemann 一函數來證明的。

: 定理：在 n³ 和 (n+1)³-1 之間，必有一個質數存在，（n>A，任何整數）

然後依此定理我們可以定義出一列質數，用此來決定 θ 之值。因為每一個 n 一定有一個對應的質數，我們可以令 p₁>A，質數 p_n，對 n=1,2, $\cdots\cdots$ 。令 p_n+1 是這樣的質數使 p_n³ < p_n+1 < (p_n+1)^{3^-n}-1 再造出二個數列， u_n=p_n^{3^-n}， v_n=(p_n+1)^{3^-n}。

但

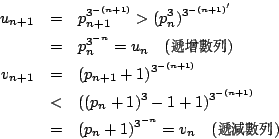
$\begin{eqnarray*} u_{n+1}&=&p_{n+1}^{3^{-(n+1)}}>(p_n^3)^{3^{-(n+1)'}}\\ &=&p_n... ...nus0.1pt{\fontfamily{cwM0}\fontseries{m}\selectfont \char 127}}) \end{eqnarray*}$

於是

$\begin{displaymath}u_1<\cdots\cdots<u_n<v_n<v_{n-1}<\cdots\cdots<v_1\end{displaymath}$

u_n 是遞增數列，v_n 是遞減數列。故應有一個極限， $\theta,\Phi,$ 即是 $u_n,\theta<\Phi\leq V_n$ （任何 n）

$\begin{displaymath} u_n^{3n}=p_n<\theta^{3^n}<(p_n+1)=V_n^{3^n} \end{displaymath}$

因而 $[\theta^{3^n}]=p_n$ ，是一個質數了。（ $[\quad]$ 仍表最大整數函數）

可是，這條定理，一如像 $f(n)=\sin{\pi}\frac{(1+(n-1)!)}{n}$ 公式，無甚用處。上面證明中顯出，對θ的知識和對所有質數的知識基本上是相等。如果我們不認得隨意大的質數，那麼別談構成θ了；但若我們認得隨意大的質數，我們不需要這條公式了。就是說，這條定理不會告訴我們新的質數。若要這條定理有用處，一定要不用質數便可以找到的值，但看起不像有此可能。

同樣的，我們可以這樣結構θ，來定出p_n質數 $(n=1,2,\cdots\cdots)$ 。若p_n代表第n個質數，使

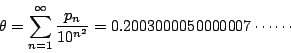
$\begin{displaymath} \theta=\sum_{n=1}^{\infty} \frac{p_n}{10^{n^2}}=0.2003000050000007\cdots\cdots \end{displaymath}$

則

$\begin{displaymath} p_n=[10^{n^2}\theta]-10^{2n-1}[10^{(n-1)^2}\theta] \end{displaymath}$

(Moser(1950),Sierpinski(1952),Härtter(1961))這亦是一條用公式寫出所有「已知」的質數之方法。正如我們在以前指出，這個公式僅是可玩而已， (聰明人說他可以做任何事的詭辯也)，對找新質數並無用處。相信類似的質數公式還有很多。例如根據Bertrand的猜測，當n大過2以後，在n和2n之間，一定有一個質數。因此可證一質數代表定理：

可以找到一個實數θ，使 $[2^{\theta}]$ , $[2^{2^{\theta}}]$ , $[2^{2^{2^{\theta}}}] \cdots$ 皆為質數。

問題當然仍在這個 θ 不易找到而已。定理只證明了它的存在性，也和以前的定理一樣，依賴以前對質數的知識。

利用 Wilson 定理：

$\begin{displaymath} \frac{(n-1)!+1}{n} = \begin{cases} \mbox{{\fontfamily{cwM1}... ...ontfamily{cwM1}\fontseries{m}\selectfont \char 98}} \end{cases}\end{displaymath}$

可以寫成

$\begin{displaymath} \cos^2{\pi(\frac{(n-1)!+1}{n})} = f(n) \begin{cases} =1, & \... ...ontfamily{cwM1}\fontseries{m}\selectfont \char 98}} \end{cases}\end{displaymath}$

所以，若 $\Pi(x)$ 為少於或等於 x 的質數數目，則

$\begin{displaymath} \Pi(x)=\sum_{2\leq n \leq x}[f(n)] \end{displaymath}$

(D)歷史上著名的「質數」數列

質數既然是重要且又難求，歷代不少數學家皆想發現一個簡單明瞭的公式，把所有質數囊括下來，如若不能，也希望發現一個公式，它的函數值永遠是質數。

我們以前介紹過多項式的表現法，此外還有其他難以下定論的各種函數，現往羅列出來。

: (1) 階乘函數列 f₁(n)=n!+1

我們容易得到， f₁(1)=2,f₁(2)=3,f₁(3)=7,但f₁(4)=25不是質數，f₁(6)=721，也不是，但 f₁(11)=11!+1=39916801是質數。f₁變化很大，我們不知道f₁(27)=27!+1是否為質數。這個數列到現在還未曾證明，是否只表現有限幾個質數而已。由此推論，(n!)²+1,n!-1，也可以構成一些質數數列了。

: (2) Catalan 數列 Cp_n+1

令Cp₀=2，而 Cp_n+1=2^Cp_n-1，是否對所有n皆成質數？ Cp₁=2²-1=3,Cp₂=2³-1=7, Cp₃=2⁷-1=127,Cp₄=2¹²⁷-1皆是質數。但 Cp₅=2^(2¹²⁷-1)-1是一個非常大的數目。 $Cp_5=2^{253}-1\approx10^{33}$ 一時還不能知道它是否為質數。因而 Cp_n-1 是否永遠為質數，想也不容易解決。

: (3) Cullen 數列 C_n=n2ⁿ+1

C₁=3,C₂=9,C₃=25 ,C₄=65,C₅=161 ,C₆,C₇,C₈,C₉,C₁₀ 皆不是。這數字也不易分解，但出現質數不多的樣子。略改一下，T_n=n2ⁿ+7，則有 T₁=9,T₂=15 不是，但 T₃=31,T₄=71,T₅=167 都是。 T₆=391不是，T₇=903 不是，T₈,T₉ 不是，但 T₁₀=10247 又是了。 T_n=n2ⁿ+7是否有無限質數以此形式出現呢？

回到Cullen數列，二十年以前，仍以為它都是「合成數」，不可能包含質數。R.M. Robinson在1957年找到， n=141時， $141 \cdot 2^{141}+1$ 是個質數，問題改觀。

英人C. Hooley在《Application of Sieve methods to the theory of number》(1976)中，曾用篩法計算。若 n2ⁿ+1 為一質數的上限值來算出這類數列中幾乎所有數目都是合成數。並討論 (2ⁿ+n²) 亦然。

: (4)冪函數數列 $S_n=2^{2^{\cdot^{\cdot^{2}}}}+1$ (n個平方)

因 S₀=2,S₁+5,S₂+17,S₃=2¹⁶+1=65537都是質數。但 2^2¹⁶+1=S₄不是，有一個因數 $2^{19} \cdot 1575+1=825753601$ ，故不可能永遠是質數，究竟這個數列會不會包含無限個質數呢？

同樣，數列 $2^{2^{\cdot^{\cdot^{2}}}}+3$ ，有 $5,19,65539 \cdots$ 也不知道是否含有無窮質數。反之，數列 $2^{2\cdots 2}+5$ 有 7,9,21,65541，不會再有質數。因 $2^{2^{2^k}}+5=2^{3t+1}+5=(7+1)^t \cdot 2+5$ 為 7 所整除，同樣 $2^{2\cdots 2}-3$ 則為 13 所整除。

: (5)費瑪數列 F_n=2^2ⁿ+1(Fermat numbers)

已知 F₀=3,F₁=5,F₂=17,F₃=257,F₄=65537皆是質數。除此外，並未發現任何新的費瑪型質數，故有人已懷疑是否仍存在 $2^{2^n}+1,n \geq 5$ 的費瑪型質數了。例如 $F_5=641 \cdot 6700417=4,294,967,297=2^{32}+1$ 在高速電算機沒有建立以前，人們用筆算算出了下列 n 值 F_n 都不是質數， 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 18, 19, 23, 36, 38, 39, 58, 63, 73。今日利用電算機，則可以查察到，下列 n 值的 F_n 數列 77, 81, 117, 125, 144, 150, 207, 226, 228, 260, 267, 268, 284, 316, 452, 1954 皆是合成數，由於 f_n 值的合成關係，我們可見其間多的是空隙，例如 F₁₉₄₅=2^2¹⁹⁴⁵+1 這個數之位數高達 10⁵⁸² 個是已知最大的一個合成數，當然不可能寫出全貌，但已知 m=(5 x 2¹⁹⁴⁷+1) 是它一個因數，這個數字也有587位，還知道它也是一個質數呢：(參看 Sierpinski 的整數論問題) 要查 F_n 是否為質數，我們可以證明：(Lucas 定理1878) F_n 的每一個自然數因數，都必是 $(2^{n+2} \cdot k+1)$ 之型， $k \geq 0$ 為一整數。如用此定理，可以獲得 F₅ 有一個 $(5\cdot 2^7+1)=641$ 的質數因子，F₆ 則有 $1071\cdot 2^8+1$ 的質數因子。此外如 F₉,F₁₀,F₁₁,F₁₂,F₁₅,F₁₆ 都有此類質因數如 $F_{16}=(3150\cdot2^{18}+1)$ 的因子，在1953年發現。可是，在n值很大， F_n的質因數 k x 2ⁿ⁺²+1太大了，一般不易一一檢證每一個k值，例如F₇和F₈便是。蓋 F₇=2²⁷+1有39位，不易查搜。J.C.Morehead在1905年用定理：

如 F_n 是質數，則 3^{2^2ⁿ-1}+1 為 F_n 所整除。

因而證明了F₇整除了3²¹²⁷+1，但仍不知道質因數。直到1971，Morrison和 Brillhart 用電算機算出

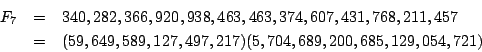
$\begin{eqnarray*} F_7&=&340,282,366,920,938,463,463,374,607,431,768,211,457\\ &=&(59,649,589,127,497,217)(5,704,689,200,685,129,054,721) \end{eqnarray*}$

Beriler的《Recreation》一書中曾將 $n \leq 73$ 以下所有F_n的已知因數列出來。

: (6)研究F_n亦是數學家認為一件好玩的事，我們附錄一件已知事實在下面，以供參考。

: a. $F_n(n \geq 2)$ ，最末數字均為7。
: b.若2^m+1為一質數，則一定是費瑪數，即m一定是2ⁿ形式。
: e. $\prod_{1\leq n< m} F_n=F_1\cdots\cdots F_n=(F_m-2)$
: f.F_n和F_k互質，即 $(F_n,F_k)=1,n \neq k$ ，因此證明質數無窮。
: g.F_n是否包含無窮個質數？仍是未知。
: h.從F_n數推出，形如nⁿ+1或n^nⁿ+1之質數。

(nⁿ+1) 為質數的充要條件是 n=2^{2^r}，r>0整數，且F_1+2^r為質數。在30萬位數以下，只有 1¹+1=2,2²+1=5,4⁴+1=257是質數，其他都是合成數。但由於 F₂₀,F₃₇,F₇₀, $\cdots F_{1034}\cdots$ ，都未查出是否為合成數，我們還不知道其他性質。若n^nⁿ+1為質數；如 1^1¹+1=2,2^2²+1=17，則一定要 (n^nⁿ+1)=F[r+2^{(r+2^r)}]。目前只知在10¹⁸ 位數以下，只有n=1，和n=2二個質數。還有沒有其他呢？

: (7)梅仙涅數列 2ⁿ-1(Mersenne Numbers)

梅仙涅數列也是古今用來找尋質數最常見的數列之一，現在所知的梅仙涅質數M_n，一共有二十四個，如2²-1=5,2³-1=7 $,\cdots\cdots$ 即是 M_n,n=2,3,5,7,13,17,19,31,61,89,107,127,共12個，是電算機末發明前算出來的。

在1952年以前，最大的質數是

$\begin{displaymath} 2^{127}-1=170,141,183,460,469,231,731,687,303,715,884,105,72... ...us0.2pt{\fontfamily{cwM0}\fontseries{m}\selectfont \char 80}}) \end{displaymath}$

M_n,n=521,607,1279,2203,2281,3217,4253,4423,9889,9941,11213,19937

都是1952年以後再發現的。

容易證明，如F_n=2^m+1為質數，則m=2ⁿ，故F_n=2^2ⁿ+1。

同樣，如M_n=aⁿ-1為質數，則a要為2，n為質數，故M_n=2^p-1。

這個數列最先是由法國數學家Mersenne在1644年提出來的。

雖然這數列仍是目前利用電算機來找尋最大的質數之途徑， (像M₉₉₄₁是一個2993位數， M₁₁₂₁₃是一個3376位數，而M₁₉₉₃₇是一個6002位數字)

據最新報導，(請參考《趣味數學》雜誌，中譯見《科學月刊》四月號)

梅仙涅數最近又發現了幾個：第二十五個和第二十六個是1978年10月由高速計算機找到的。第25個是 p=21707,M₂₁₇₀₇=2²¹⁷⁰⁷-1 第26個是 p=23209,M₂₃₂₀₉=2²³²⁰⁹-1 最新一個是第27個，1979年由D.Slowinski發現的。

$\begin{displaymath} p=24497,\mbox{ {\fontfamily{cwM3}\fontseries{m}\selectfont \char 185}}M_{24497}=2^{24497}-1 \end{displaymath}$

即他的位數為 $24497\cdot \log{2}=24497\times 0.3010$ 約近於7373位數字，想來也大得可以了。但直到現在，我們還不能知道是否有無數個梅仙涅質數呢! 下面列出一些有關的定理。

a. 若p為一質數，則M_p的每一個自然數因子必為(2kp+1)型的數字， ( $k \geq 0$ 整數)，如M₁₁的因子就是(22k+1)，k=0,1,4，因此 M₁₁=2047 =1 x 23 x 89，可是M₁₀₁雖被證明為一合成數，且只有二個質數因子，但仍不知道其分解式。

b. $p \leq 257$ ，M_p的分類如下：

: (甲)質數：2,3,5,7,13,17,19,31,61,89,107,127
: (乙)全被分解的合成數：11,23,29,37,41,43,47,53,59,67,71,73,79,83,97, 103,113,151,163,179,181
: (丙)合成數，二個以上因子已知：173,191,223,229,233,239,251
: (丁)合成數，只知道一個因子：109,131,157,167,193,197,211,241
: (戊)合成數，但不知任何因子：101,137,139,149,199,227,257

例如

: (甲) M₈₉=61897001964269013744956211 (質數)
: (乙) M₁₁₃=2¹¹³-1=3391 x 23279 x 65993 x 1868569 x 1066818132868207
: (丙) $M_{239}=479\cdot 1913\cdot 5737\cdot 176383 \cdot 1374000609\times ?$
: (丁) M₂₄₁=22000409 x ?
: (戊) M₂₅₇=2²⁵⁷-1， M₁₃₇=2¹³⁷-1 都是合成數，但因子不知。

c.定理：若p是(8k+7)型質數，則p整除 $M_{\frac{p-1}{2}}$

例如47整除M₂₃，479整除M₂₃₉，503整除M₂₅₁

(附加條件還要 $\frac{p-1}{2}$ 同是一個(4k+3)型的質數才是)

d. Lucas-Lehmer數列：4,14,194,37634, $\cdots\cdots$
即

u₁=4,u_n=u_n-1²-1

可用這個數列來檢定M_n是否為質數。

$\begin{displaymath}M_n \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 1... ...tfont \char 98}} \Leftrightarrow M_n=2^{n}-1, M_n \vert u_{n-1}\end{displaymath}$

(這個定理是充份且必要之條件。故此，當不對時，M_n便為合成數了。)

例如其中第四項 u₄=u_3-1²-2=194²-2=37634，定被M₅=2⁵-1=31所整除，因此M₅=31為質數。有人計算M₁₀₁不能整除u₁₀₀。故M₁₀₁應是合成數。若

$\begin{displaymath} V_n=(1+\sqrt{3})^n+(1-\sqrt{3})^n \quad (n \geq 1) \end{displaymath}$

則

$\begin{displaymath} V_{2^k}=2^{2^{k-1}}u_k(k\geq 1) \end{displaymath}$

由於u_n都是偶數，上述數列可改為： $t_1=2,t_{k+1}=2t_k^2-1 (k \geq 1)$ 即

$\begin{displaymath} t_{k+1}=\frac{1}{2} u_{k+1}=2(\frac{u_k}{2})^2-1 \end{displaymath}$

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強

最後修改日期：4/26/2002