微積分與差和分大意 (第 4 頁)

　1│2│3│4　

微積分與差和分大意
連續與離散之間的類推（第 4 頁）

蔡聰明

首頁 | 搜尋

．原載於數學傳播第二卷第二期
．作者當時任教於台大數學系
‧對外搜尋關鍵字

四、差和分與微積分之間的類推關係

除了上述二、三節所列差分、和分與微分、積分的基本性質具有類推外，現在我們要再列出更多的類推關係。我們也要注意兩者之間的差異處，以及類推不成立的情況。換句話說，我們不但要小心分辨「異中之同」，也要小心分辨「同中之異」。

(甲)Taylor展開公式

這分別有離散與連續的類推。它是數學中「逼近」這個重要想法的一個特例。逼近想法的意思是這樣的：給一個函數 f，我們要研究 f 的行為，但 f 本身可能很複雜而不易對付，於是我們就想法子去找一個較「簡單」的函數 g，使其跟 f 很「靠近」，那麼我們就用 g 來取代 f。這又是以簡御繁的精神表現。由上述我們看出，要使用逼近想法，我們還需要澄清

兩個問題：即如何選取簡單函數及逼近的尺度。

(一) 對於連續世界的情形，Taylor 展式的逼近想法是選取多項函數作為簡單函數，並且用局部的「切近」作為逼近尺度。說得更明白一點，給一個直到到 n 階都可導微的函數 f，我們要找一個 n 次多項函數 g，使其跟 f 在點 x₀ 具有 n 階的「切近」，即 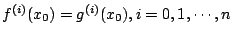$f^{(i)}(x_0)=g^{(i)}(x_0),i=0,1, \cdots , n$ ，答案就是

$\begin{displaymath} g(x)=f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)^2 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \end{displaymath}$

此式就叫做 f 在點 x₀ 的 n 階 Taylor 展式。

g 在 x₀ 點附近跟 f 很靠近，於是我們就用 g 局部地來取代 f。從而用 g 來求得 f 的一些局部的定性行為。因此 Taylor 展式只是局部的逼近。當f是足夠好的一個函數，即是所謂解析的函數時，則 f可展成 Taylor 級數，而且這個 Taylor 級數就等於 f 自身。

值得注意的是，一階 Taylor 展式的特殊情形，此時 g(x)=f(x₀+f'(x₀)(x-x₀)) 的圖形正好是一條通過點 (x₀,f(x₀)) 而且切於 f 的圖形之直線。因此 f 在點 x₀ 的一階 Taylor 展式的意義就是，我們用過點 (x₀,f(x₀)) 的切線局部地來取代原來 f 曲線。這種局部化「用平直取代彎曲」的精神，是微分學的精義所在。

利用 Talor 展式，可以幫忙我們做很多事情，比如判別函數的極大值與極小值，求積分的近似值，作函數表（如三角函數表，對數表等），這些都是意料中事。事實上，我們可以用逼近的想法將微積分「一以貫之」。

復次我們注意到，我們選取多項函數作為逼近的簡單函數，理由很簡單：在眾多初等函數中，如三角函數，指數函數，對數函數，多項函數等，從算術的觀點來看，以多項函數最為簡單，因為要計算多項函數的值，只牽涉到加減乘除四則運算，其它函數就沒有這麼簡單。

當然，從別的解析觀點來看，在某些情形下還另有更有用更重要的簡單函數。例如，三角多項式，再配合上某種逼近尺度，我們就得到 Fourier 級數展開，這在應用數學上佔有舉足輕重的地位。（事實上，Fourier 級數展開是採用最小方差的逼近尺度，這在高等數學中經常出現，而且在統計學中也有應用。）

: 註：取 x₀=0 的特例，此時 Taylor 展式又叫做 Maclaurin 展式。不過只要會做特例的展開，欲求一般的 Taylor 展式，作一下平移（或變數代換）就好了。因此我們大可從頭就只對 x=0 點作 Taylor 展式。

(二) 對於離散的情形，Taylor 展開就是：

給一個數列 $(f_t)_{t\in z}$ ，我們要找一個 n 次多項式數列 (g_t)，使得 g_t 與 f_t 在 t=0 點具有 n 階的「差近」。所謂在 0 點具有 n 階差近是指：

$\begin{displaymath}f_0=g_0, \triangle f_0=\triangle g_0, \cdots , \triangle^n f_0=\triangle^n g_0\end{displaymath}$

答案是

$\begin{displaymath}g_t=f_0+\triangle f_0t^{(1)}+\frac{\triangle^2 f_0}{2!}t^{(2)} + \cdots + \frac{\triangle^n f_0}{n!} t^{(n)}\end{displaymath}$

此式就是離散情形的 Maclaurin 公式。

(乙)分部積分公式與Abel分部和分公式的類推

(一) 分部積分公式:

設 u(x),v(x) 在 [a,b] 上連續，則

$\begin{displaymath} \int^b_a udv = (uv) \big\vert^b_a-\int^b_a vdu \end{displaymath}$

(二) Abel分部和分公式:

設(u_n),(v)為兩個數列，令 s_n=u₁+......+u_n，則

$\begin{displaymath}\sum^{n-1}_{k=1}u_kv_k=\sum^{n-1}_{k=1}(\triangle s_{k-1})v_k=s_{n-1}v_n-\sum^{n-1}_{k=1}s_k\triangle v_k\end{displaymath}$

上面兩個公式分別是萊布尼慈導微公式 D(uv)=(Du)v+u(Dv)，及萊布尼慈差分公式 $\triangle(u_kv_k)=(\triangle u_k)v_{k+1}+u_k(\triangle v_k)$ 的結論。注意到，這兩個萊布尼慈公式，一個很對稱，另一個則不然。

(丙)微分方程根本定理與差分分程定理的類推

(一) 微分方程根本定理是說：若 y'=O 則 y 必為常函數。

（例：用它可以證明一階微分方程 y'=ky 的解答必形如 y=y(0)e^kt）

(二) 差分方程很本定理是說：若 $\triangle y_n=0$ ，則 y_n 必為常數列。

（例：用它可以證明一階差分方程 $\triangle y_n=ky_n$ 的解答必形如 y_n=y₀(1+k)ⁿ）

(丁)複利與連續複利 (這也分別是離散與連續之間的類推)

(一) 複利的問題是這樣的：有本金 y₀，年利率 r，每年複利一次，要問 n 年後的本利和 y_n=? 顯然這個數列滿足差分方程

y_n+1=y_n(1+r)

根據(丙)之(二)得知

y_n=y₀(1+r)ⁿ

這就是複利的公式。

(二) 若考慮每年複利 m 次，則 t 年後的本利和應為

$\begin{displaymath}y(t)=y_0(1+\frac{r}{m})^{mt}\end{displaymath}$

令 $m\rightarrow \infty$ ，就得到連續複利的概念，此時本利和為

$\begin{displaymath}y(t)=\lim_{m\rightarrow \infty}y_0(1+\frac{r}{m})^mt=y_0e^{rt}\end{displaymath}$

換句話說，連續複利時，t 時刻的本利和 y(t)=y₀e^rt 就是微分方程

y'=ry

的解答。

由上述我們看出離散複利問題由差分方程來描述，而連續複利的問題由微分方程來描述。對於常係數線性的差分方程及微分方程，解方程式的整個要點就是疊合原理，因此求解的辦法具有完全平行的類推。

(戊)Fubini 重和分定理與 Fubini 重積分定理(也是離散與連續之間的類推)

(一) Fubini 重和分定理：給一個兩重指標的數列 (a_rs)，我們要從 r=1 到 m，s=1到 n, 對 (a_rs) 作和 $\sum^{m,n}_{r,s=1}a_{rs}$ ，則這個和可以這樣求得：光對 r 作和再對 s 作和（反過來亦然）。亦即我們有

$\begin{displaymath}\sum^{m,n}_{r,s=1}a_{rs}=\sum^{m}_{r=1}(\sum^{n}_{s=1}a_{rs})=\sum^{n}_{s=1}(\sum^{m}_{r=1}a_{rs})\end{displaymath}$

(二)Fubini 重積分定理：設 f(x,y) 為定義在 $\Omega=[a,b]\times[c,d]$ 上之可積分函數，則

$\begin{displaymath}\int_\Omega f=\int^b_a(\int^d_cf(x,y)dy)dx=\int^d_c(\int^b_a f(x,y)dx)dy\end{displaymath}$

當然，變數再多幾個也都一樣。

(己)Lebesgue 積分的概念

(一) 離散的情形：給一個數列 (a_n)，我們要估計和 $\sum^{n}_{i=1}a_i$ ，Lebesgue 的想法是，不管這堆數據指標的順序，我們只按數值的大小來分堆，相同的分在一堆，再從每一堆中取一個數值，乘以該堆的個數，整個作和起來，這就得到總和。

(二)連續的情形：給一個函數 f，我們要定義曲線 y=f(x) 跟 X 軸從 a 到 b 所圍出來的面積。（見下圖）

Lebesgue 的想法是對 f 的影域 $[\alpha,\beta]$ 作分割：

$\begin{displaymath} \alpha=y_0<y_1< \cdots <y_{i-1}<y_i< \cdots <y_n=\beta \end{displaymath}$

函數值介 y_i-1 到 y_i 之間的 x 收集在一齊，令其為 $A_i=\{x\vert y_{i-1}\leq f(x)<y_i\}$ ， $i=l, \cdots , n$ 於是 [a,b] 就相應分割成 $\Omega = A_1 + \cdots + A_n$ ，取樣本點 $x_i\in A_i$ ，作近似和

$\begin{displaymath} \sum f(x_i)\times(A_i\mbox{ {\fontfamily{cwM1}\fontseries{m}... ...us0.1pt{\fontfamily{cwM1}\fontseries{m}\selectfont \char 25}}) \end{displaymath}$

讓影域的分割加細，上述近似和的極限若存在的話，就叫做 f 在 [a,b] 上的 Lebesgue 積分。

以上我們只敘述粗略的大綱，至於詳細情形講參閱楊維哲、蔡聰明編著的《普通數學教程》（文仁出版社印行）一書。

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：洪瑛 ∕ 校對：黃信元 ∕ 繪圖：簡立欣

最後修改日期：5/6/2002