已在第一頁　1│2│3│4　次頁

 		 


首頁 | 搜尋

．作者任教於香港科技大學數學系
 

《基礎幾何學》
五、向量幾何和向量代數
——空間結構的系統代數化

項武義

 
 

在空間中由 A 到 B 的有向直線段 $\overrightarrow{AB}$ 其本身就是 A, B 兩點所標記的兩個位置之間的差別 (difference between the locations of A and B) 的具體化描述；而 位移向量 (displacement vector) 則是將這種「位置差別」 加以定量化所定義的基本幾何量。它的本質內涵是 $\overrightarrow{AB}$ 的方向和長度。換句話說，當兩個有向直線段 $\overrightarrow{AB}$ 和 $\overrightarrow{A'B'}$ 為同向平行而且等長時，兩者所表達的位移向量定義為相等。另一方面，空間中的平移變換把空間中每一個點作同向等距的移動，由此可見位移向量本質上就是平移的另一種表達。總之，位移向量和平移是同一事物的兩種觀點，前者著眼于其所表達的位置移動，而後者則著眼于它是空間一種特殊的保長變換。


位移向量的基本性質

【定義】：若空間中的一個變換 τ 滿足條件

\begin{displaymath}\overrightarrow{P\,\tau(P)} \; \mbox{{\fontfamily{cwM0}\fonts... ...nt \cH16}\z{\fontfamily{cwM2}\fontseries{m}\selectfont \cH197}}\end{displaymath}

則稱 τ 為空間的一個平移 (translation) 。

【定理 5.1】： 設 A, B 為空間中任給兩點，則存在一個唯一的平移 τ 使得 $\tau(A)=B$（我們將以 $\tau(A,B)$ 記之）。

証明：先証存在性：

若 A=B，則恆等變換即為所求者。

若 $A\neq B$，令 $\Pi_1$, $\Pi_2$ 分別是和直線段 $\overline{AB}$ 正交于 A 和 M（M 是 $\overline{AB}$ 的中點）的平面，則 ${\mathfrak R}_{\Pi_2}\circ{\mathfrak R}_{\Pi_1}$ 這個反射對稱的組合即為所求者。

再証唯一性：

設 P 是空間中任給一點，τ 是上述所作的平移，而 $\tau'$ 則是一個將 A 映射到 B 的平移，我們所要証明者是 $\tau'(P)=\tau(P)$ 。由所設 $\overrightarrow{P\tau'(P)}$, $\overrightarrow{P\tau(P)}$ 都和 $\overrightarrow{AB}$ 同向平行而且等長。因為過 P 點和 $\overrightarrow{AB}$ 平行的直線是唯一存在的，所以 $\tau'(P)=\tau(P)$ 。由于 P 是任給的，所以 $\tau'$ 和 τ 是同一個變換。 □

【定理 5.2】：設 $\tau_1$, $\tau_2$ 是空間的兩個平移，則 $\tau_2\circ\tau_1$ 也是一個平移，而且 $\tau_2\circ\tau_1=\tau_1\circ\tau_2$ 。

証明：在此我們將採用簡約符號 $A'=\tau_1(A)$, $A''=\tau_2(A')=\tau_2\circ\tau_1(A)$ 。由所設，對于空間任給兩點 A, B 恆有

\begin{displaymath}\overrightarrow{AA'} \; \mbox{ {\fontfamily{cwM0}\fontseries{... ...0}\fontseries{m}\selectfont \cH184} } \; \overrightarrow{B'B''}\end{displaymath}

各別同向平行而且等長，而我們所要証明者則是 $\overrightarrow{AA''}$ 和 $\overrightarrow{BB''}$ 也必然同向平行而且等長。其証明如下：


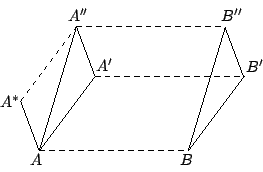
\begin{displaymath} \xy \xyimport(5,5){\epsfxsize=5cm \epsfbox{fig0501.eps}}*\fr... ...{A'} ,(4.7,5.4)*+{B''} ,(3.7,-0.3)*+{B} ,(5.2,3.4)*+{B'} \endxy\end{displaymath}

[ 圖 5-1 ]

如 [圖 5-1] 所示，連結 $\overrightarrow{AB}$, $\overrightarrow{A'B'}$ 和 $\overrightarrow{A''B''}$ 。由平面幾何中熟知的平行四邊形特徵性質可見，

\begin{displaymath}\hskip-3pt\raise-1pt\hbox{\xy\xyimport(1,1){\epsfxsize=0.6cm ... ...=0.6cm \epsfbox{pgram.eps}}*\frm{} \endxy }\hskip-1ptA'B'B''A''\end{displaymath}

兩者都是平行四邊形，所以

\begin{displaymath}\overrightarrow{AB} \; \mbox{ {\fontfamily{cwM0}\fontseries{m... ...}\fontseries{m}\selectfont \cH184} } \; \overrightarrow{A''B''}\end{displaymath}

都是同向平行而且等長，即 $\overrightarrow{AB}$ 和 $\overrightarrow{A''B''}$ 也是同向平行而且等長的，因此 $\hskip-3pt\raise-1pt\hbox{\xy\xyimport(1,1){\epsfxsize=0.6cm \epsfbox{pgram.eps}}*\frm{} \endxy }\hskip-1ptABB''A''$ 乃是一個平行四邊形。所以就証明了 $\overrightarrow{AA''}$ 和 $\overrightarrow{BB''}$ 也是同向平行而且等長的，亦即 $\tau_2\circ\tau_1$ 也是一個平移。

再証： $\tau_1\circ\tau_2 = \tau_2\circ\tau_1$

令 $A^*=\tau_2(A)$，則有 $\overrightarrow{AA^*}$ 和 $\overrightarrow{A'A''}$ 同向平行而且等長。同理， $\hskip-3pt\raise-1pt\hbox{\xy\xyimport(1,1){\epsfxsize=0.6cm \epsfbox{pgram.eps}}*\frm{} \endxy }\hskip-1ptAA'A''A^*$ 也是一個平行四邊形，即有 $\overrightarrow{A^*A''}$ 和 $\overrightarrow{AA'}$ 同向平行而且等長，所以

\begin{displaymath}\tau_1\circ\tau_2(A)=\tau_1(A^*)=A''=\tau_2\circ\tau_1(A)\end{displaymath}

而 A 是空間任給一點，亦即 $\tau_1\circ\tau_2$ 和 $\tau_2\circ\tau_1$ 是相同的變換。 □

【定義與符號】：定義上述和次序無關的平移組合 $\tau_1\circ\tau_2 = \tau_2\circ\tau_1$ 為 $\tau_1$, $\tau_2$ 之和 (sum)，將改用符號 $\tau_1+\tau_2$ 表示之。再者，往後我們將改用粗體小寫字母如 ${\bf a}$, ${\bf b}$, ${\bf c}$, ${\bf x}$, ${\bf y}$ 等表示位移向量。 採取這種符號， $\tau(B,C)\circ\tau(A,B)=\tau(A,B)\circ\tau(B,C)=\tau(A,C)$ 就可以寫成 ${\bf a}+{\bf b}={\bf c}$，或者 $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ 。

[註]：在加法符號下，我們把恆等變換這個特殊的平移 $\tau_0$ 改用 ${\bf0}$ 來表示，因為對于任何平移 τ，恆有 $\tau_0\circ\tau=\tau\circ\tau_0=\tau$ ，而這個事實在加法符號下即為

\begin{displaymath}{\bf0}+{\bf a}={\bf a}+{\bf0}={\bf a}\end{displaymath}

再者 $\overrightarrow{AB}$（亦即 $\tau(A,B)$ ）的逆變換就是 $\overrightarrow{BA}$（亦即 $\tau(B,A)$ ），而且有

\begin{displaymath}\tau(A,B)\circ\tau(B,A)=\tau_0=\tau(B,A)\circ\tau(A,B)\end{displaymath}


\begin{displaymath}(\overrightarrow{AB}+\overrightarrow{BA}=\overrightarrow{AA}= \overrightarrow{BB}=\overrightarrow{BA}+\overrightarrow{AB})\end{displaymath}

所以記 $-\overrightarrow{AB}=\overrightarrow{BA}$（即 $-\tau(A,B)=\tau(B,A)$），亦即

\begin{displaymath}(-{\bf a})+{\bf a}={\bf0}={\bf a}+(-{\bf a})\end{displaymath}

 
對外搜尋關鍵字：
．平移
．Eudoxus
．相似變換
．勾股定理
．內積
．Hamilton
．四元數
．複數
．協變
．Menelous定理
．Ceva定理
．Ceva
．圓冪定理

已在第一頁　1│2│3│4　次頁

 回頁首
 
（若有指正、疑問……，可以在此 留言 或 寫信 給我們。）
EpisteMath

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有


最後修改日期：6/19/2004