| |
【例題】:
- (1)
- P, Q, R 三點共線的向量條件式:
設 P, Q, R 三點共線,O 是任選之原點,即如 [圖 5-6] 所示:
[ 圖 5-6 ]
則存在實數 k,使得
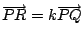 ,亦即 ,亦即
換言之,存在有不全為零的系數 α, β, γ 滿足
反之,若存在滿足上述條件的 α, β, γ(設
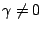 ),即有 ),即有
- (2)
- 用向量代數証明 Menelous 定理:
[ 圖 5-7 ]
令
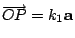 , ,
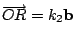 , ,
 。首先,由 A, B, Q
三點共線的向量條件式,即有 。首先,由 A, B, Q
三點共線的向量條件式,即有
再者,由 P, Q, R 三點共線的向量條件式,即有
由此解得
所以
即得
- (3)
- 重心和 Ceva 定理:
[ 圖 5-8 ]
設
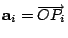 分別為質量 分別為質量 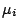 的三個質點的位置向量,則其重心的位置向量就是
的三個質點的位置向量,則其重心的位置向量就是
其中 mi 是 Pi 的質量百分比(亦即
m1+m2+m3=1)。若改用重心作為原點,則
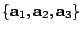 滿足條件式 滿足條件式
由
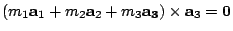 得 得
這其實乃是 Ceva 定理在「力學」中的表現。
- (4)
- 圓冪定理的向量証法:
設 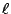 為過 P 點的直線,與圓交于 Q1, Q2 兩點。令 X 為 為過 P 點的直線,與圓交于 Q1, Q2 兩點。令 X 為
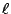 上的一個動點, 上的一個動點,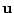 是沿 是沿 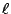 方向的單位長向量。 方向的單位長向量。
[ 圖 5-9 ]
易見有
由此可見,直線 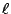 上的動點 X 恰好位于以 O 為圓心,半徑為
R 的圓上的條件式就是 上的動點 X 恰好位于以 O 為圓心,半徑為
R 的圓上的條件式就是
上述二次方程式的兩個根 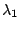 , ,  也就是 也就是
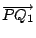 和
和
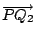 的有向長度。所以 的有向長度。所以
第一式的幾何意義就是
第二式的幾何意義是什麼呢?
令 P' 是 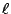 上使得 (PP',Q1Q2) 成調和點列之點,亦即 上使得 (PP',Q1Q2) 成調和點列之點,亦即
設
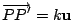 ,則有 ,則有
所以
上述向量代數式的幾何意義就是:
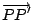 在直線 OP
上的垂直投影是一個固定的向量,亦即和 在直線 OP
上的垂直投影是一個固定的向量,亦即和 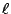 無關。 無關。
[ 圖 5-10 ]
【習題】:
- (1)
- 試驗証在例題 (1) 中當
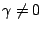 的條件換成 的條件換成 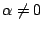 或
或 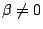 時,同樣結論亦成立。 時,同樣結論亦成立。
設  , , 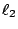 是空間中兩條(相異)直線, 是空間中兩條(相異)直線,
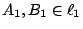 , ,
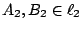 為線上給定的(相異)四點。令 X1, X2 分別為 為線上給定的(相異)四點。令 X1, X2 分別為  , ,
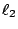 上的動點,則容易把 上的動點,則容易把
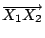 改寫成下述形式: 改寫成下述形式:
- (2)
- 問
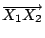 同時垂直于 同時垂直于  , , 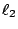 的代數條件式是什麼?
的代數條件式是什麼?
- (3)
- 試討論在什麼的情況下這個公垂線段
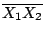 是 是
- (i)
- 唯一存在的,而且其長度不為 0;
- (ii)
- 唯一存在的,但是其長度為 0;
- (iii)
- 並非唯一存在的。
- (4)
- 令
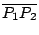 為題 (3)(i) 情形中的公垂線段。試証這是所有 為題 (3)(i) 情形中的公垂線段。試証這是所有
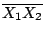 中的最短者。 中的最短者。
|
|
|