畢氏定理的兩個推廣 (第 2 頁)

　1│2│3│4│5　

畢氏定理的兩個推廣（第 2 頁）

蔡聰明

首頁 | 搜尋

．原載於科學月刊第二十五卷第十二期
．作者當時任教於台大數學系
‧對外搜尋關鍵字

四面體的餘弦定理

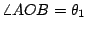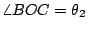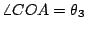考慮一般的四面體 OABC，如圖八。令OA=a，OB=b，OC=c， $\angle AOB = \theta_1$ ， $\angle BOC = \theta_2$ ， $\angle COA = \theta_3$ ，這六個量唯一決定了四面體 OABC。再令

$\begin{displaymath} \overrightarrow{OA}=\vec{u} , \overrightarrow{OB}=\vec{v} , \overrightarrow{OC}=\vec{w} , \end{displaymath}$

最初步我們可以猜測，(15)式應該修正成下形：

$\begin{displaymath} (\triangle ABC)^2=(\triangle OAB)^2+(\triangle OBC)^2 + (\triangle OCA)^2 - f(a,b,c,\theta_1,\theta_2,\theta_3) \eqno{(16)} \end{displaymath}$

其中 f 是六個變數的函數，它的精確公式可不可以由一些線索猜測得到？

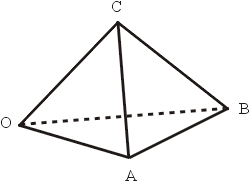
圖八

最容易知道的兩條線索（即特例）是：

(i)直角四面體的情形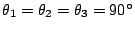： $\theta_1=\theta_2=\theta_3=90^{\circ}$ ，此時

$\begin{displaymath} f(a,b,c,\theta_1,\theta_2,\theta_3)=0 \eqno{(17)} \end{displaymath}$

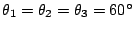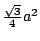(ii)正四面體的情形： $\theta_1=\theta_2=\theta_3=60^{\circ}$ ，且a=b=c，此時每一面的面積皆為 $\frac{\sqrt{3}}{4} a^2$ ，故欲(16)式成立，必然

$\begin{displaymath} f(a,b,c,\theta_1,\theta_2,\theta_3)=\frac{3}{8} a^4 \eqno{(18)} \end{displaymath}$

要決定一個六變數的函數，談何容易！幸好，我們還有最後的一招：向量演算的硬工夫。

因為 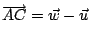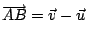$\overrightarrow{AC}=\vec{w}-\vec{u}$ ， $\overrightarrow{AB}=\vec{v}-\vec{u}$ ，所以

$\begin{eqnarray*} &&(\triangle ABC)^2 \\ &=&( \frac{1}{2}\parallel (\vec{w}-\ve... ...ac{1}{2} (\vec{v}\times \vec{u}) \cdot (\vec{u}\times \vec{w}) \end{eqnarray*}$

由 Lagrange 等式 [(8)式] 得知：

$\begin{eqnarray*} && (\vec{w}\times \vec{v}) \cdot (\vec{v}\times \vec{w}) + (... ...inus0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 50})} \end{eqnarray*}$

從而，

$\begin{displaymath} \begin{eqalign} & f(a,b,c,\theta_1,\theta_2,\theta_3) \\ &... ...eta_1}-\cos{\theta_2}\cos{\theta_3})] \end{eqalign}\eqno{(19)} \end{displaymath}$

我們很容易驗知，此式符合(17)與(18)兩式之特例。

總結上述，我們得到

定理四(四面體的餘弦定律)：

對於四面體 OABC，恆有

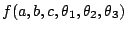$\begin{displaymath} \begin{eqalign} (\triangle ABC)^2 &= (\triangle OAB)^2 + (\t... ... -f(a,b,c,\theta_1,\theta_2,\theta_3) \end{eqalign}\eqno{(20)} \end{displaymath}$

其中 $f(a,b,c,\theta_1,\theta_2,\theta_3)$ 如(19)式。

注意：如果不用向量演算，那麼上述的計算會變得非常冗長。

在三角學裡有所謂的解三角形問題，此地我們也有解四面體的問題。

問題一：如本節開頭所述，已知四面體的 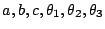$a,b,c,\theta_1,\theta_2,\theta_3$ （見圖八），試解四面體。即求：三個稜線長、四個面的面積，四面體的體積、三個立體角、六個兩面角、九個稜線夾角。

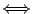問題二：在四面體中，試證任何三個面的面積和大於第四面的面積。等號成立 $\Longleftrightarrow$ 有一個頂點落到對面三角形中。

Schneebeli[8] 給出了另一種形式的四面體之餘弦定律：

定理五(四面體的餘弦定律)：

設OABC為一個四面體，以 OA,OB,OC 為共同稜的兩面角分別為α,β,γ (見圖九)，則

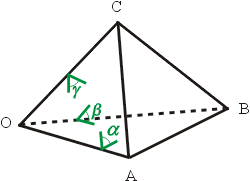
$\begin{displaymath} \begin{eqalign} (\triangle ABC)^2 &= (\triangle OAB)^2 + (\... ...e OAB \cdot \triangle OBC \cos \beta) \end{eqalign}\eqno{(21)} \end{displaymath}$

圖九

這個定理的證明，只需要用到向量的內積與外積演算以及

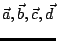$\begin{displaymath} \vec{a} + \vec{b} + \vec{c} + \vec{d} = 0 \eqno{(22)} \end{displaymath}$

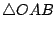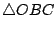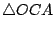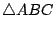其中向量 $\vec{a}, \vec{b}, \vec{c}, \vec{d}$ 分別代表四面體各面向外的法向，且其大小分別為 $\triangle OAB$ 、 $\triangle OBC$ 、 $\triangle OCA$ 與 $\triangle ABC$ 之面積。

　1│2│3│4│5　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強 ∕ 繪圖：簡立欣

最後修改日期：2/17/2002