前面的討論可以推廣到三元,四元……聯立方程式上,但並不很容易。尤其推廣到多元時,每次要寫那麼多個方程式,那麼多係數,也夠煩人了。煩人不但浪費時間,往往還看不清要點。許多科學的進展,都基於公式的簡潔。因此,在進一步探討前,先設法把符號簡化一下。
例如,我們有三元聯立方程組:
(這兒不用 x,y,z 而用 x1,x2,x3 也是為了方便。注意:x2 不是 x 的二次方。這裏我們只涉及一次,應不會產生誤解。)我們能不能設法寫成一個式子呢?
當然可以!符號只不過是符號,任由人規定。我們可將之規定為:
按方程組的秩序排列。再規定 A「乘」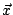 為: 為:
乘的結果是和 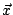 , ,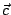 等類似的東西,由三個數排成(注意:
A11 x1+A12 x2 + A13 x3 只是一個數)。這相當於三度空間中的一個向量(從原點到三個數代表的那一點)。我們用 等類似的東西,由三個數排成(注意:
A11 x1+A12 x2 + A13 x3 只是一個數)。這相當於三度空間中的一個向量(從原點到三個數代表的那一點)。我們用
代表三個方程式,便要求 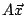 這個向量的三個分向量分別和 這個向量的三個分向量分別和 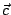 的三個分向量(為 c1,c2,及 c3)相等。這也正是向量代數的規定。 的三個分向量(為 c1,c2,及 c3)相等。這也正是向量代數的規定。
這樣,聯立方程組的問題,等於是向量空間上的問題。用向量空間的眼光來看,
表示 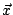 這個向量被 A 乘了後,變成另一個向量 這個向量被 A 乘了後,變成另一個向量 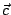 。
這兒,A 把一個向量變換 (Transform) 成另個向量,便管它叫做變換矩陣 (Transformation Matrix,所以叫做矩陣,是因為它是矩形──正方形是矩形的特例)。解聯立方程組,便等於說,我們有個變換矩陣 A,有個特定的向量 。
這兒,A 把一個向量變換 (Transform) 成另個向量,便管它叫做變換矩陣 (Transformation Matrix,所以叫做矩陣,是因為它是矩形──正方形是矩形的特例)。解聯立方程組,便等於說,我們有個變換矩陣 A,有個特定的向量 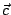 ,要求出一個向量 ,要求出一個向量 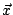 ,它剛好被 A 變換成 ,它剛好被 A 變換成 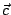 。 。
變換的實例太多了。把一個向量,以某一定方向為軸旋轉個角度是個例子。高中解析幾何中所討論座標軸的旋轉便是此類。(高三讀者當會知道,適當的轉軸可以把曲線方程式化成簡單形式)。把向量沿某些方向延長或縮短若干倍也是種變換;把個向量變為負向量(即所有分向量均乘負號)也是一種;把向量投影在某一座標軸(或任何方向)也是一種(以上諸種,參見圖I)。其他如把每一向量加一特定已知向量,把某兩個座標軸互相對調,等等。
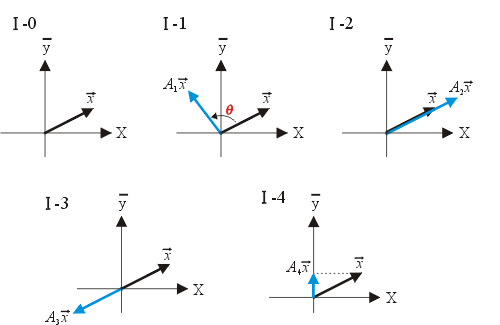
圖I:幾種變換的例子:1. A1 旋轉;2. A2 放大;3. A3 原點反射;4. A4 y 軸投影
|
在各種變換中,可大概分為二類。一類是可逆的,例如旋轉 θ 角,再反轉同樣角度,就回復到原來向量。一類是不可逆的,例如投影,有無數個向量投影到同一向量,我們便分辨不出原來是由那個向量投影的(見圖II)。因此,投影這種變換是不可逆的。
解聯立方程組
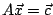 ,等於求一個向量 ,等於求一個向量 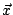 ,它會被 A 變換成 ,它會被 A 變換成 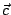 。從上面分析,我們知道 。從上面分析,我們知道 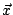 等於 A 的反變換(記作 A-1)作用在 等於 A 的反變換(記作 A-1)作用在 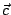 上: 上:
這樣,解聯立方程便變為求反變換了。
我們知道,聯立方程組未必有解,這相當於那個變換是不可逆的。這類變換,數學上管它叫做奇異的 (Singular),可逆的便是非奇異的 (Non-singular)。
|