淺談 Stokes' 定理與電磁學 (第 3 頁)

　1│2│3│4│5　

淺談 Stokes' 定理與電磁學（第 3 頁）

邵錦昌
記錄：李啟鈴

首頁 | 搜尋

．原載於數學傳播第十八卷第四期
．作者當時任教於交大應數系
‧對外搜尋關鍵字

3. Maxwell's Equations

Faraday 定律發現之後, 再經過一、二十年左右, Maxwell 把這三個現象整理出四個方程式出來, 這就是有名的Maxwell's Equations, 最後就變成整套的電磁理論。

Maxwell's equation:

$\begin{displaymath}\cases{ \nabla \cdot \overrightarrow{E}=4 \pi \rho&\qquad\qqu... ...hfill (11)\cr \nabla \cdot \overrightarrow{B}=0&\hfill (12)\cr}\end{displaymath}$

這四個方程式, 兩個是關於電場的divergence 和curl, 另外兩個是關於磁場的divergence和curl。所有的電磁現象, 例如:日光燈的發亮、收音機、…等, 全部可以用這四個方程式來解釋, 這四個方程式是由先前的三個現象導出來的,導的過程主要是利用Stokes' 和Gauss定理, 還有一些向量的計算。導出這四個偏微分方程式之後, 剩下的問題,差不多就是數學家的問題。其中第一個方程式是和庫侖定律有關, 第三個是和Faraday定律有關, 剩下的兩個則是和Biot-Savart定律有關。前面兩個式子很容易可以用Stokes';或Gauss定理導出, 比較麻煩的是由Biot-Savart定律導出另外兩個式子, 這裡我們要稍微提一下, Biot-Savart定律並不完全等於這兩個式子, 這中間還有一些需要討論, 所以在這三個實驗現象和Maxwell's Equations 之間還有一些東西需要補起來, 補這個東西的人當然就是Maxwell, 所以這些方程式,一般就叫做Maxwell's Equations。那麼下面我們就開始用這三個現象, 經過Gauss和Stokes'定理來把Maxwell's Equations建立起來。

3.1 從Coulomb定律到第一個Maxwell's Equation

首先我們來看庫侖定律, 庫侖定律告訴我們, 如果我們有兩個電荷, 它們之間就有作用力, 而這個力符合反平方定律, 我們把這個公式寫得稍微詳細一點:

$\begin{displaymath}\overrightarrow{F}=q_1q_2 {\overrightarrow{r_2} - \overrighta... ...ert\overrightarrow{r_2} - \overrightarrow{r_1}\vert^3}\eqno(13)\end{displaymath}$

這個意思就是, 我們在空間中先選好一個座標原點, 再給座標 $\hat{e_1}$ 、 $\hat{e_2}$ 、 $\hat{e_3}$ , 然後假設q₁ 是在 $\overrightarrow{r_1}$ 的位置上, $\overrightarrow{r_1}$ 就是從座標原點到 q₁ 的位置, q₂ 是在 $\overrightarrow{r_2}$ 的位置上, $\overrightarrow{r_2}-\overrightarrow{r_1}$ 很容易可以看出來是q₁ 到 q₂ 的這個向量(如圖6)

圖6

所以 $\overrightarrow{F}$ 是指 q₂ 所受的力, 方向在 $\overrightarrow{r_2}-\overrightarrow{r_1}$ 上, 大小是和反平方成比例。

3.1.1. 電場

為了研究方便起見, 我們不妨在(13)式中 q₂ 的位置放一個單位電荷, 因為所受的力與電荷大小成比例, 所以只要用單位電荷來研究就可以了, 放了單位電荷之後, 這個力我們就叫做電場, 電荷放在不同的位置, 電場的大小與方向也會變, 所以就把它看成是 $\overrightarrow{r_2}$ 的函數, 然後將 $\overrightarrow{r_2}$ 改寫成 $\overrightarrow{r}$ 就得到

$\begin{displaymath}\overrightarrow{E}(\overrightarrow{r})=q_1 \cdot {\overrighta... ...ert\overrightarrow{r}-\overrightarrow { r _1}\vert^3} \eqno(14)\end{displaymath}$

這就是電場的定義。如果我們在空間中多放一些電荷,根據實驗, 這些電荷作用在單位電荷上的力是遵守一個原理叫做 Linear superposition principle, 換句話說, 如果我們有電荷 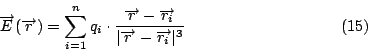$q_1, q_2, \cdots, q_n$ , 那麼這個單位電荷所受的力就是

$\begin{displaymath}\overrightarrow{E}(\overrightarrow{r})=\sum^{n}_{i=1}q_i \cdo... ...{\vert\overrightarrow{r}-\overrightarrow{r_i}\vert^3} \eqno(15)\end{displaymath}$

同樣地, 磁場也是遵守Linear superposition principle, 由於Maxwell's equations 要解的就是電場和磁場, 而我們出發點已經用了線性的原理, 所以我們得到的方程式都是線性的, 當然自然界的其它現象並沒有這麼簡單, 例如核子力就絕不是線性的, 所以現在物理學家所面對的問題是非線性的。

有的時候我們所討論的問題是一堆電荷可以像物質一樣, 而物質是由分子構成的, 不過分子很小, 當它很多又分佈的很密的時候, 我們可以用連續體的觀念來看它, 如果電荷也是這樣的話, 我們不妨介紹一個電荷密度ρ的觀念, 現在把q_i用ρ表示, 和改成積分, $\overrightarrow{r_i}$ 改成 $\overrightarrow{r}^{'}$ , 然後這個電場公式就是

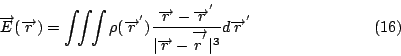
$\begin{displaymath}\overrightarrow{E}(\overrightarrow{r})=\int\!\!\int\!\!\int \... ...errightarrow { r^{'}}\vert^3}d \overrightarrow{r}^{'} \eqno(16)\end{displaymath}$

3.1.2 推導過程

現在我們來求 $\overrightarrow{E}$ 的divergence, 我們不妨以(15)式逐項來看, 經由直接計算, 我們很容易可以證明當 $\overrightarrow{r} \neq \overrightarrow{r_{i}}$ 時, $\nabla \cdot\overrightarrow{E}=0$ 。然後我們把中間一個量拿來做面積分

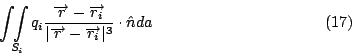
$\begin{displaymath}\int \!\! \int\limits_{S_i} q_i {\overrightarrow{r}-\overrigh... ...ow{r}-\overrightarrow{r_{i}}\vert^3} \cdot \hat{n} da \eqno(17)\end{displaymath}$

這個面S_i怎麼取呢? 假設有很多個電荷 q₁, q₂, $\cdots, q_i, \cdots$ , 對於q_i電荷, 我們取一個以q_i為球心的小球面(如圖7)

圖7

使得這個球只包含q_i一個電荷,然後在球面上做面積分, 因為 $\overrightarrow{r}$ 在球面上, 那麼 $\overrightarrow{r}-\overrightarrow{r_i}$ 就在 $\hat{n}$ 的方向上,假設球的半徑為d, 則

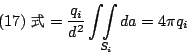
$\begin{displaymath}\mbox{(17) {\fontfamily{cwM1}\fontseries{m}\selectfont \char 31}} = {q_i\over d^2} \int \!\! \int\limits_{S_i} da=4 \pi q_i\end{displaymath}$

現在假設有q₁,q₂,…,q_n個電荷, 然後做一個大體積V, 將所有的電荷都包含在裡面, V的邊界叫做A, 我們對 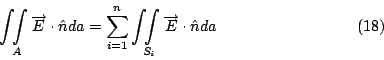$\overrightarrow{E} \cdot \hat{n}$ 做面積分, 這個面積分等於每個小球面S_i的面積分和

$\begin{displaymath}\int \!\! \int\limits_A \overrightarrow{E} \cdot \hat{n}da= \... ...! \int\limits_{S_i} \overrightarrow{E} \cdot \hat{n}da\eqno(18)\end{displaymath}$

原因是如果將兩式相減, 這整個的積分可以看成是一個曲面S的積分, 現在的S就是把V扣掉各個小球之後, 所得到的體積V^'的邊界, 然後根據Gauss定理, 這整個曲面上的積分,就會等於 $\int\!\int\!\int\limits_{V'}\nabla \cdot \overrightarrow{E}d^3 x$ , 而在這個V^'上的 $\nabla \cdot\overrightarrow{E}=0$ ,所以這個積分值就等於0, 移項之後就得到(18)式。又這些小球面上的積分等於 $4 \pi q_i$ , 所以 $\int\!\int\limits_A\overrightarrow{E} \cdot \hat{n}da=4 \pi\sum^{n}_{i=1}q_i$ , 這就是有名的Gauss Law。其實歷史上Gauss應該是先處理靜電學上的問題, 然後才把數學公式抽離出來,也就是Gauss定理。

剛剛我們處理的是一個一個的電荷, 現在把它推廣到有連續電荷分佈的狀況, 這時候電荷的和, 可以寫成 $\int\!\int\!\int\limits_V\rho(\overrightarrow{r})d^3 \overrightarrow{r}$ ,所以Gauss Law就變成

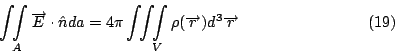
$\begin{displaymath}\int \!\! \int\limits_A \overrightarrow{E} \cdot \hat{n}da= 4... ...mits_V \rho(\overrightarrow{r})d^3 \overrightarrow{r} \eqno(19)\end{displaymath}$

因為左邊是一個向量場的面積分, 我們可以再用一次Gauss定理, 它就等於 $\int \!\! \int \!\! \int\limits_V \nabla \cdot \overrightarrow{E} d^3 x$ , 然後再前後對照一下, 因為這裡的A是任意取的, 所以 $\nabla \cdot \overrightarrow{E}=4 \pi \rho (\overrightarrow{r})$ , 這就是第一個Maxwell's Equation。

3.2. 由 Biot-Savart 定律導出第二個和第四個 Maxwell's Equation

接著我們再討論Biot-Savart定律, 這比較麻煩一點, 在討論之前, 我們先來介紹一下電流

3.2.1. 電流

剛剛討論的是靜電學的東西, 也就是電荷靜止的狀況, 但是當然電荷也會動, 電荷動會有新的現象發生, 所以現在我們要考慮到電荷動的情況, 事實上電荷動的情形跟質點流動的情形一樣, 因此我們可以學習流體力學, 定義電流密度 $\overrightarrow{J}$ , $\overrightarrow{J}$ 的方向在電流流動的方向 $\hat{n}$ 上, 如果N表示單位體積內的電荷個數, q表示每個電荷的電荷量, v是電荷速度, 則

$\begin{displaymath}\overrightarrow{J}=N \cdot q \cdot v \cdot \hat{n}\eqno(20)\end{displaymath}$

如果空間中有電荷在流動, 我們可以做一個小面積A(如圖8),

圖8

然後利用 $\overrightarrow{J}$ 來求單位時間通過A的電荷量, 得到

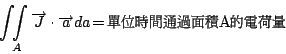
$\begin{displaymath}\int \!\! \int\limits_A \overrightarrow{J} \cdot \overrightar... ...nus0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 190}}\end{displaymath}$

式中 $\overrightarrow{J} \cdot \overrightarrow{a}$ 是 $\overrightarrow{J}$ 在法線方向上的分量。一般而言, 我們平常用的電線的截面積A差不多都是相同的, 而且很小, 所以電線上的電流I=JA。

現在來看 $\overrightarrow{J}$ 和ρ的關係, 因為我們總是假設電荷是保守的, 也就是電荷不會產生也不會消失, 所以假設空間中有電荷在流動, 取一個封閉曲面A(如圖9),

圖9

這時候A裡面的電荷量, 就等於 $\int\!\int\!\int\limits_V \rho d^3 x$ , 又因為電荷在流動, 所以這裡面的電荷量會改變,這變化的增加或減少, 完全是由於電荷的流進或流出, 這就可以用 $\overrightarrow{J}$ 來算, 因此

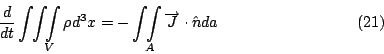
$\begin{displaymath}{d\over dt} \int \!\! \int \!\! \int\limits_V \rho d^3 x = - ... ... \!\! \int\limits_A \overrightarrow{J} \cdot \hat{n}da\eqno(21)\end{displaymath}$

因為習慣上取 $\hat{n}$ 為向外的方向, 所以流出算正, 流入算負, 不過, 電荷量的導數, 增加時為正, 減少時為負, 所以上式中有一負號。但是右邊又是一個面積分, 因此可以再用一次Gauss定理, 就得到 $-\int\!\int\!\int\limits_V \nabla \cdot \overrightarrow{J}d^3x$ , 又A是任意取的, 所以等式對於任意V 都成立,於是得到

$\begin{displaymath}{\partial \rho\over \partial t}+\nabla \cdot \overrightarrow{J}=0\eqno(22)\end{displaymath}$

其實這個式子跟電磁學並沒有深入的關係, 只不過是一般的Conservation Law而已。

3.2.2. Biot-Savart定律的討論

我們來看一下Biot-Savart定律為什麼是(7)式這種樣子, 作實驗時, 我們放兩個線圈I₁和I₂, 分取下一段 $d\ell_1$ 和 $d \ell_2$ (如圖10)

圖10

這兩段的電流是 $I_1 d \ell_1$ 和 $I_2 d \ell_2$ , 我們先看這兩個小電流中間的作用力, 這個作用力和 $I_1 d \ell_1$ 、 $I_2 d \ell_2$ 成比例, 這和剛剛靜電力與q₁、q₂成比例是一樣的, 所以 $I_1 d \ell_1$ 和 $I_2 d \ell_2$ 就是剛剛的q₁和q₂, 而 $\overrightarrow{r}/r^3$ 就是剛剛的反平方定律, 只不過方向比剛剛要複雜多了, 力的方向並不在兩點的連線上。現在將 $d\ell_1$ 和 $d \ell_2$ 取下來看(如圖11)

圖11

$d \overrightarrow{\ell_1} \times \overrightarrow{r}$ 的方向指向紙內(利用右手定則), 我們將它定義成磁場 $\overrightarrow{B}$ , 接著再看 $\overrightarrow{B}$ 對 $d \overrightarrow{\ell_2}$ 的作用, 如果我們做一個Biot-Savart定律的實驗, 將磁鐵放(如圖12)

圖12

那麼就有一個磁場 $\overrightarrow{B}$ , 假如中間有一個電荷, 它靜止不動的話, 則它不受力, 若它在動的話, 它會受一個力, 這個力的方向和大小跟 $\overrightarrow{v} \times \overrightarrow{B}$ 成比例, 所以力的方向與 $\overrightarrow{v}$ 且與 $\overrightarrow{B}$ 垂直。剛剛我們已經定義了一個磁場 d $\overrightarrow{\ell_1}$ × $\overrightarrow{r}$ , 當然這個定義需要跟磁鐵做比較, 實驗的結果是一樣的, 而 $d \overrightarrow{\ell_2}$ 可以看成是一個電荷在運動, d $\overrightarrow{\ell_2}$ 就像 $\overrightarrow{v}$ 一樣, 所以最後的力就會與 d $\overrightarrow{\ell_2}$ × $(d \overrightarrow{\ell_1}$ × $\overrightarrow{r})$ 成比例, 再把這些小線段加起來, 就是這兩個線積分。

磁力和電力不大一樣, 磁力的方向並不在連線的方向上, 而在垂直的方向上, 所以磁力不作功, 而電力作功。

接著要把(7)式推廣到一般的情形, 因為我們要導一般電磁學的定律, 當然不能只用在線圈的電流上, 而是用在一般的電荷運動上, 首先, 我們研究所謂stationary的情形, 也就是電荷及電流不隨時間變動, 所以 ${\partial \rho\over \partial t}=0$ , 根據(22)式, 得到 $\nabla \cdot \overrightarrow{J}=0$ 。在一般的情形時, 因為I等於J乘上面積, 而面積再乘上 $d \ell$ 就變成體積分, 所以公式可以寫成

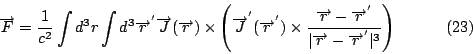
$\begin{displaymath} \overrightarrow{F}={1\over c^2}\int d^3 r \int d^3 \overrigh... ...rightarrow{r}-\overrightarrow{r}^{'} \vert^3} \right) \eqno(23)\end{displaymath}$

$\begin{displaymath}c: \mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 10... ...\fontseries{m}\selectfont \char 167}}=2.9 \times 10^{10} cm/sec\end{displaymath}$

當我們在做Biot-Savart定律的實驗時, 因為一開始在Coulomb定律的時候, 就有電荷,從電荷又定義了電荷密度, 所以一切單位從這邊一直過來, 都已經固定了, 我們去量兩個線圈的作用力時, 發覺這個力相當的小, 所以當這些單位全部固定的時候, 有一個比例常數,實驗的結果它等於1/c², c正好等於光速,因此這個力比靜電力小多了, 到目前為止, c與光速一致只是巧合而已。現在我們來看一下Biot-Savart 定律如何導出(10)和(12)式。

第四個 Maxwell's equation 的導出

首先, 我們利用(23)式來定義磁場, 所以將 $\overrightarrow{F}$ 寫成

$\begin{displaymath}\overrightarrow{F}={1\over c}\int d^3 \overrightarrow{r} \ove... ...row{r}) \times \overrightarrow{B}(\overrightarrow{r}) \eqno(24)\end{displaymath}$

假設有兩堆電荷在流動, 一堆 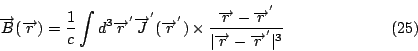$\overrightarrow{J}(\overrightarrow{r})$ , 另一堆 $\overrightarrow{J}^{'} (\overrightarrow{r}^{'} )$ , 這兩堆流動的電荷就有作用力, 根據實驗的結果就得到(23)式, 然後把 $\overrightarrow{r}^{'}$ 這部份的積分叫做 $\overrightarrow{B}(\overrightarrow{r})$ , 也就是 $\overrightarrow{r}^{'}$ 這部份電荷流動所產生的磁場, 它在 $\overrightarrow{J}(\overrightarrow{r})$ 所做的力就是 $\overrightarrow{F}$ , 然後比較兩式,

$\begin{displaymath}\overrightarrow{B}(\overrightarrow{r})={1\over c}\int d^3 \ov... ...vert\overrightarrow{r}-\overrightarrow{r}^{'} \vert^3}\eqno(25)\end{displaymath}$

這就是電流產生磁場的定義。底下我們用到一個公式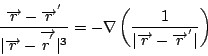

$\begin{displaymath}{\overrightarrow{r}-\overrightarrow{r}^{'} \over \vert\overri... ...r \vert\overrightarrow{r}-\overrightarrow{r}^{'} \vert} \right)\end{displaymath}$

所以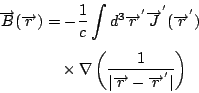

$\begin{displaymath} \begin{eqalign} \overrightarrow{B}(\overrightarrow{r}) &= -{... ...ghtarrow{r}-\overrightarrow{r}^{'} \vert} \right) \end{eqalign}\end{displaymath}$

然後我們再用一個向量的公式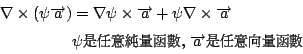

$\begin{displaymath} \begin{eqalign} \nabla \times (\psi \overrightarrow{a}) &= \... ...tfamily{cwM1}\fontseries{m}\selectfont \char 98}} \end{eqalign}\end{displaymath}$

我們把 $\overrightarrow{J}^{'} (\overrightarrow{r}^{'} )$ 當成 $\overrightarrow{a}$ , ${1}{\vert\overrightarrow{r} - \overrightarrow{r}^{'} \vert}$ 當成 ψ，但 $\overrightarrow{J}^{'} (\overrightarrow{r}^{'} )$ 是 $\overrightarrow{r}^{'}$ 的函數, 而 $\nabla$ 則是對 $\overrightarrow{r}$ 而言，所以 $\nabla \times \overrightarrow{a}=0$ ，因此 $\nabla \times (\psi \overrightarrow{a})=\nabla \psi \times \overrightarrow{a}$ ,

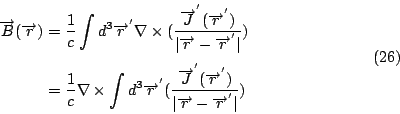
$\begin{displaymath} \begin{eqalign} \overrightarrow{B}(\overrightarrow{r}) &= {... ...rrow{r}-\overrightarrow{r}^{'} \vert}) \end{eqalign} \eqno(26) \end{displaymath}$

可是, 對任意向量函數 $\overrightarrow{A}, \nabla \cdot (\nabla \times \overrightarrow{A})=0$ , 這一來的話 $\nabla \cdot \overrightarrow{B}=0$ , 我們就得到Maxwell's equations 的第四個方程式。如果把 $\nabla \cdot \overrightarrow{B}=0$ 與第一個方程式 $\nabla \cdot \overrightarrow{E}=4 \pi \rho$ 做比較的話, 我們可看出它的意義, 因為 $\nabla \cdot \overrightarrow{E}=4 \pi \rho$ , 所以 $\nabla \cdot \overrightarrow{E}$ 可以表示出電場的來源, 可是 $\nabla \cdot \overrightarrow{B}=0$ , 意思是說我們有electric charge, 可是我們並沒有magnetic charge。到了後來, 二十世紀的物理學家Dirac, 硬是要討論也有magnetic charge的情況, 這就是有名的monopole理論, 而且不管理論或實驗討論的非常多, 內容也很多, 但這是屬於另外的範圍。

3.2.4. 第二個 Maxwell's equation 的推導

現在我們來看第二個 Maxwell's equation, 利用(26)求 $\overrightarrow{B}$ 的 curl

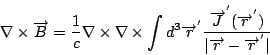
$\begin{displaymath}\nabla \times \overrightarrow{B}={1\over c} \nabla \times \na... ...'} )\over \vert\overrightarrow{r}-\overrightarrow{r}^{'} \vert}\end{displaymath}$

計算這個式子, 我們利用一個向量恆等式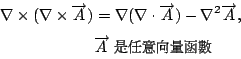

$\begin{displaymath} \begin{eqalign} \nabla \times (\nabla \times \overrightarrow... ...tfamily{cwM1}\fontseries{m}\selectfont \char 98}} \end{eqalign}\end{displaymath}$

其中

$\begin{displaymath} \nabla^{2} = \left( {\partial^2\over \partial {x_1}^2}+ {\pa... ...\partial {x_2}^2} + {\partial^2\over \partial {x_3}^2} \right) \end{displaymath}$

所以

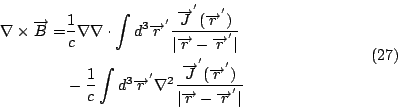
$\begin{displaymath} \begin{eqalign} \nabla \times \overrightarrow{B} = &{1\over ... ...w{r}-\overrightarrow{r}^{'} \vert} \cr \end{eqalign} \eqno(27) \end{displaymath}$

我們先看第一項

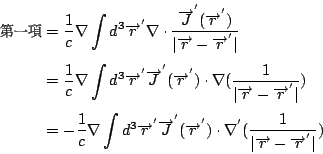
$\begin{displaymath} \begin{eqalign} \mbox{{\fontfamily{cwM2}\fontseries{m}\selec... ...overrightarrow{r}-\overrightarrow{r}^{'} \vert} ) \end{eqalign}\end{displaymath}$

接著再用另一個向量恆等式

$\begin{displaymath}\nabla \cdot (\psi \overrightarrow{a}) =\overrightarrow{a}\cdot \nabla^{'} \psi + \psi \nabla^{'} \cdot \overrightarrow{a}\end{displaymath}$

我們把 ${1\over \vert\overrightarrow{r}-\overrightarrow{r}^{'} \vert}$ 當做 ψ, 把 $\overrightarrow{J}^{'} (\overrightarrow{r}^{'} )$ 當做 $\overrightarrow{a}$ 得到

$\begin{displaymath} \mbox{{\fontfamily{cwM2}\fontseries{m}\selectfont \char 15}\... ...vert\overrightarrow{r}- \overrightarrow{r}^{'} \vert} \right] \end{displaymath}$

因為第一個積分是某一個向量場的 divergence 的積分, 這樣又可以用 Gauss 定理, 可是現在積分的範圍是任意的, 是包含所有電荷的任意範圍, 當然可以將這個範圍推到 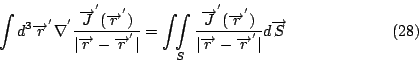$\infty$ 去, 所以我們得到

$\begin{displaymath}\int d^3 \overrightarrow{r}^{'} \nabla^{'} {\overrightarrow{J... ...{r}-\overrightarrow{r}^{'} \vert} d \overrightarrow{S}\eqno(28)\end{displaymath}$

這個面 S 可以推到 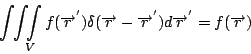$\infty$ 去, 而在 $\infty$ 的地方,我們都假設物理量為 0, 否則,整個宇宙的能量會變成 $\infty$ , 至於宇宙的能量我們相信是有限的, 所以(28) 式等於0, 而我們在做 Biot-Sovart 定律實驗時, 我們又假設了 stationary case, 因此, $\nabla^{'} \cdot\overrightarrow{J}^{'} (\overrightarrow{r}^{'} )$ 等於0, 我們就得到第一項整個等於0; 關於第二項, 我們使用底下這個式子

$\begin{displaymath} \nabla^2 {1\over \vert\overrightarrow{r}-\overrightarrow{r}^... ...rt} =-4 \pi \delta(\overrightarrow{r}-\overrightarrow{r}^{'} ) \end{displaymath}$

其中 $\delta(\overrightarrow{r}-\overrightarrow{r}^{'} )$ 是所謂的 Dirac δ 函數，具有下面的性質，即對於任意函數 $f(\overrightarrow{r})$

$\begin{displaymath} \int\!\!\int\!\!\int\limits_V f(\overrightarrow{r}^{'} ) \d... ...tarrow{r}^{'} )d \overrightarrow{r}^{'} =f(\overrightarrow{r}) \end{displaymath}$

其中 $\overrightarrow{r}$ 包含在體積 V 之內。關於這部份我們不說明得太詳細了, 總之

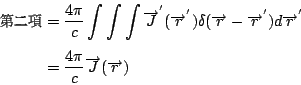
$\begin{displaymath} \begin{eqalign} \mbox{{\fontfamily{cwM2}\fontseries{m}\selec... ...{4 \pi}{c} \overrightarrow{J}(\overrightarrow{r}) \end{eqalign}\end{displaymath}$

所以，就得到(27)式， $\nabla \times \overrightarrow{B}=\frac{4 \pi}{c}\overrightarrow{J} (\overrightarrow{r})$ 。這個式子和第二個 Maxwell's equation 有一些差別，這是最有趣的一部份，我們等一下再來談它。

3.3. 由 Faraday 定律到第三個 Maxwell's Equation

根據實驗的結果, Faraday 定律是

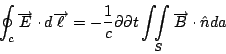
$\begin{displaymath} \oint_c \overrightarrow{E} \cdot d \overrightarrow{\ell} = ... ... t} \int\!\!\int\limits_S \overrightarrow{B} \cdot \hat{n} da \end{displaymath}$

又由 Stokes' 定理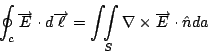

$\begin{displaymath} \oint_c \overrightarrow{E} \cdot d \overrightarrow{\ell} = \... ...\int\limits_S\nabla \times \overrightarrow{E} \cdot \hat{n} da \end{displaymath}$

比較上面兩式, 而且這個曲面 S 是任意的, 所以就得到第三個 Maxwell's equation

$\begin{displaymath}\nabla \times \overrightarrow{E} + {1\over c} {\partial \overrightarrow{B}\over \partial t}=0\end{displaymath}$

這一部份是相當簡單的。

3.4. Faraday 的修正 Maxwell's Equation

整個綜合起來, 我們差不多已經得到 Maxwell's equations 了。可是比較一下我們所得到的四個方程式和Maxwell's equaitons，我們發現 $\nabla \times \overrightarrow{B}$ 不一樣， $-{1\over c}{\partial \overrightarrow{E}\over\partial t}$ 項沒有了，可以感覺的出來這四個方程式放在一起是不 consistent，因為只有一個跟時間有關的方程式, 別的方程式都沒有時間, 這很顯然一定有矛盾在, 所以我們知道的結果一定有缺陷, 因為我們在 Biot-Savart 的實驗時做了一個 stationary 的限制, 換句話說, 所討論的 $\overrightarrow{J}$ 是加了 $\nabla \cdot \overrightarrow{J}=0$ 的條件進去, 因此所得到的定律本身有缺陷是很自然的, 這當然要靠Maxwell的天才, 他看出這個事實,然後把它補起來。

現在看 $\nabla \times \overrightarrow{B}={4 \pi\over c} \overrightarrow{J}$ 這個式子, 如果成立的話, 則

$\begin{displaymath}\nabla \cdot \overrightarrow{J}={c\over 4 \pi} \nabla \cdot \nabla \times \overrightarrow{B} \equiv 0\end{displaymath}$

可是一般 $\nabla \cdot \overrightarrow{J}\neq 0$ 。為了要找出補救的辦法, 我們來考慮Conservation of charge, 這是一定會成立的, 所以

$\begin{displaymath}0={\partial \rho\over \partial t}+\nabla \cdot \overrightarrow{J}\end{displaymath}$

Maxwell 覺得 ρ 可以由第一個方程式得到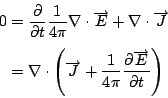

$\begin{displaymath}\rho={1\over4 \pi}\nabla \cdot \overrightarrow{E}\end{displaymath}$

因此

$\begin{displaymath} \begin{eqalign} 0 &= {\partial\over \partial t}{1\over 4 \pi... ...rtial \overrightarrow{E}\over \partial t} \right) \end{eqalign}\end{displaymath}$

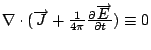一般來講 $\nabla \cdot \overrightarrow{J}\neq 0$ , 除非stationary, 但 $\nabla \cdot(\overrightarrow{J}+ {1\over 4 \pi}{\partial \overrightarrow{E}\over \partial t})\equiv 0$ , 所以Maxwell就把 $\nabla \times \overrightarrow{B}={4 \pi\over c}\overrightarrow{J} (\overrightarrow{r})$ 中的 $\overrightarrow{J}(\overrightarrow{r})$ 加上 ${1\over 4 \pi}{\partial \overrightarrow{E}\over \partial t}$ , 這時候 $\nabla \cdot \nabla \times B \equiv 0$ , 而 $\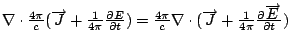nabla \cdot {4 \pi\over c}(\overrightarrow{J}+ {1\over 4 \pi} {\partial E\over... ...verrightarrow{J}+ {1\over 4 \pi} {\partial \overrightarrow{E}\over \partial t})$ 也恆等於0, 就把原來的第二個方程式修改成

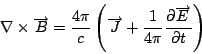
$\begin{displaymath}\nabla \times \overrightarrow{B}={4 \pi\over c} \left(\overri... ...er 4 \pi} {\partial \overrightarrow{E}\over \partial t} \right)\end{displaymath}$

再把 ${1\over c}{\partial \overrightarrow{E}\over \partial t}$ 項搬到左邊, 於是得到我們要的第二個 Maxwell's equation。 Maxwell 只是做了這樣一個簡單的變動, 結果是對的, 所有的電磁現象全部在這裡, 也就是加了 ${1\over 4 \pi}{\partial \overrightarrow{E}\over \partial t}$ 項之後, 我們由數學式子可以導出波動(wave)的現象, 可以導出輻射(radition) 的現象, 也就是一個電荷如果有加速度在動的話, 它會輻射出電波出來等等。

　1│2│3│4│5　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：康明軒 ∕ 校對：鄧惠文 ∕ 繪圖：簡立欣

最後修改日期：4/26/2002