工作不能增加利潤,則他的報酬當是 0。此人稱為冗員 (dummy),因對一個冗員 i 而言,
 恆為 0,故 恆為 0,故
 。 。
在上題中我們看到工程師與廠主的報酬相同,這似乎與事實不合,在大部分的工廠中,
工程師拿不到廠主的待遇。這個原因是在一般情形下,工程師不只一個,尤其當工程師供過於求時,他們的身價就會慘跌。現設 S={廠主,工程師甲,工程師乙,工人甲} 其代號仍依次為 1,2,3,4。
但只需一個工程師就夠了。在這時候,若廠主請了其中的一位,他仍付他二萬五?
且看公式(1)中
 的結果。 的結果。
- (1)
對空集合及含一元素之集合而言,
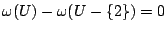 。 。
- (2)
對二元素的集合而言,只有
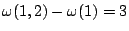 不為0。 不為0。
- (3)
對三元素的集合而言,只有
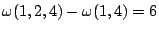 不為 0 (
U(1,2,3)-U(1,3)=3-3=0,因另一個工程師乙捷足先登,工程師甲的工作就泡了湯。) 不為 0 (
U(1,2,3)-U(1,3)=3-3=0,因另一個工程師乙捷足先登,工程師甲的工作就泡了湯。)
- (4)
對四元素之集合
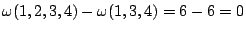 。
因此工程師甲的報酬應為 。
因此工程師甲的報酬應為
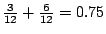 。
引用原則一,或再導一次可知工程師乙之公平所得亦為0.75,二者之和只有1.5萬,
竟然比原來一個人可得的2.5萬少了一萬。這說明了供過於求一個可怕的結果,
多一個工程師不但不能增加工程師的收入,而且拖了同仁下水。
其原因自然因為廠主有恃無恐,不怕找不到工程師而可以加以殺價的緣故。
但這個事實竟能從公平三原則中反映出來,不可不謂數學的奇蹟。
現在看看資本家與工人可因此多獲利多少。稍加計算可得 。
引用原則一,或再導一次可知工程師乙之公平所得亦為0.75,二者之和只有1.5萬,
竟然比原來一個人可得的2.5萬少了一萬。這說明了供過於求一個可怕的結果,
多一個工程師不但不能增加工程師的收入,而且拖了同仁下水。
其原因自然因為廠主有恃無恐,不怕找不到工程師而可以加以殺價的緣故。
但這個事實竟能從公平三原則中反映出來,不可不謂數學的奇蹟。
現在看看資本家與工人可因此多獲利多少。稍加計算可得
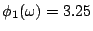 , ,
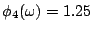 ,可見其中大部分的好處為廠主所得,
但工人也因工程師多而身價小增。依理往前推,若工程師再多,則其身價必又再跌,
原來工程師之所以可以與資本家平分秋色乃是因工程師只有一位,沒有他開不了工,
奇貨可居之故。當然若只有一個工程師而有二個工廠,
則他的身價會增加而廠主的報酬就要下跌。但在一般社會中都是資本家少,工程師多,
而勞工更多,因此工人可以分得之公平工資之慘,可以想見。 ,可見其中大部分的好處為廠主所得,
但工人也因工程師多而身價小增。依理往前推,若工程師再多,則其身價必又再跌,
原來工程師之所以可以與資本家平分秋色乃是因工程師只有一位,沒有他開不了工,
奇貨可居之故。當然若只有一個工程師而有二個工廠,
則他的身價會增加而廠主的報酬就要下跌。但在一般社會中都是資本家少,工程師多,
而勞工更多,因此工人可以分得之公平工資之慘,可以想見。
公式(1)之推導固然精彩,可惜(幸好)在一般情形下,不容易計算,
因為  含有 S 中全部的子集,有 2n 個。當 n 稍大時,計算量就會壓死計算機。但在某些情形下,特別是成員的能力大多相同時,表一中的排列法就能減少到可以計算的地步。現舉一個這樣的例子。 含有 S 中全部的子集,有 2n 個。當 n 稍大時,計算量就會壓死計算機。但在某些情形下,特別是成員的能力大多相同時,表一中的排列法就能減少到可以計算的地步。現舉一個這樣的例子。
設某鳥商請一個村子裡的人為他養鳥,各家養一隻。到收購的時候,
他宣佈他只能買成對的鳥兒,一對一千元。村人各戶人家集合算了一下,
發現有雄鳥110隻,雌鳥90隻,因此可賣九萬元,為了不使養雄鳥之家搶賣打破頭起見,
全村一氣,算大家共賣,因此得了九萬元,放生了20隻雄鳥。現在問題是錢要如何分配才「公平」。
當養雄鳥之家主張均攤,即每隻鳥值 9萬/200 = 450 元,但養雌鳥人家認為物以稀為貴,
雌鳥之所以活得少,必定是比較難養,理應多分一點,紛爭又起,如何擺平?
如果我們以謝卜勒原則看公平,則因鳥只有二種,可以求出
式中 [y] 表 y 之整數值,n1 為 i 所屬之類的鳥數,即若 i 為雄,則n1=110,i 為雌,則 n1=90,n2 另一類鳥數,n=n1+n2。用計算機算出結果是雄鳥單價值 109 元,雌鳥單價為 876 元,而全部雄鳥之值只有雌鳥的 6.5 分之一。其實稍不平衡,價差就很驚人,如果雄、雌各為 102 及 98 隻,則其單價比為 1:1.82,物以稀而貴,一致於此。
記得若干年前臺灣適婚年齡者男多女少,少女身價百倍。現在好像是女多男少,
單身漢行情看漲。不過人間的情形很複雜,我們不能把每位少男少女像鳥兒一樣看為等價。因各人條件不同,每個人的公平地位就不容易由(1)計算出來(2n子集而 ?),條件好的男女是不介意情敵多少的。但(1)式至少能解釋一個重要的現象,稍不平衡,就產生極大的價差。 ?),條件好的男女是不介意情敵多少的。但(1)式至少能解釋一個重要的現象,稍不平衡,就產生極大的價差。
其實人們雖不知公式(1),但這種現象早已深植於人們的心中,每個人都想改變自我環境,
使得公式(1)對我有利。當供過於求的時候,人們曾經把糧食、牛奶、羊毛倒入海中以求增加價格,以鳥兒為例,若雄鳥人家先商量好,偷偷放走20隻 則對養雄鳥人家都有利,
(若放走30隻則更有利,這時候雌鳥每隻只值201元而雄鳥值773元,雖全部只剩下80對鳥兒,但對雄鳥人家而言則有利。但這要合作才行,若你自己把鳥放了,則可能一文都拿不到。)各行業防止供過於求,用執照、工會、幫會、碼頭等加以限制人數。
而大家也都知道要進到一個行業中成為一個不可少的人。
然而也有些人雖不喜歡不平,但卻想破壞公平,有人破壞第一原則,利用各種關係,
使得報酬與名字有關,他是我的兒子,報酬就自然加大,有的破壞第二原則,
沒有做事的人也巧立名目,拿一些錢。當然,最壞的是鼓勵生產力不足的人用搶,
嚴重的破壞了公平的分配。
|