談公平 (第 2 頁)

　1│2│3│4　

談公平（第 2 頁）

楊照崑

首頁 | 搜尋

．原載於數學傳播第十六卷第三期
．作者當時任教於美國佛羅里達大學統計系
‧對外搜尋關鍵字

謝卜勒 (Shapley) 公平三原則

首先我們必須明白有合作才有分配公不公平的問題。否則你走你的陽關道打獵，我過我的獨木橋捕魚，在山吃山，靠水吃水，各顧自己，就談不到分配不均的問題。今令 ω 為一個可由多人合作的工作，而 S 表示可以參與工作的人們的集合。若 U 為 S 的一個子集，則 $\omega(U)$ 表示 U 人合作時可得的工作利潤。以前面工廠為例，則

$\begin{displaymath} S = \{ \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \ch... ...0.1pt{\fontfamily{cwM3}\fontseries{m}\selectfont \char 14}} \} \end{displaymath}$

若 U={廠主, 工程師} 時， $\omega(U)=3$ (萬元)，若 U={廠主, 工程師, 工人甲}，則 $\omega(U)=6$ ，若 U={廠主, 工人甲}，則 $\omega(U)=0$ ，為了簡便起見，令 S 中的元素以 1,2,…,n 為代號，即 $S = \{1,\cdots,n\}$ 。令 $\phi(\omega)$ 表示 i 成員在 ω 工作上該得的報酬。謝卜勒在1953年的論文中，訂下了三個公平的原則。

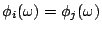原則1：報酬與名字無關，只與各人的貢獻有關。即若 i 與 j 互換而不影響 ω 時， $\phi_{i}(\omega)=\phi_{j}(\omega)$ 。

沒有人會反對這個原則，即同工應同酬，張三若可做李四的事，則張三可拿李四的報酬，與他叫張三或李四無關。

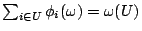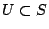原則2：利潤屬於工作者， $\sum_{i\in U} \phi_{i}(\omega)=\omega(U)$ 對所有 $U\subset S$ 均成立。

這也是一個公平的原則，U 人合得的利益，自然分給 U 裡的人。

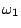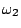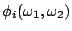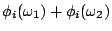原則3：若有二件工作 $\omega_1$ 與 $\omega_2$ ，則 $\phi_i (\omega_1,\omega_2)$ = $\phi_i (\omega_1) + \phi_i (\omega_2)$ 對所有 i 均成立。

這也是無人反對的公理，我做二份工作，自可得二分酬勞。

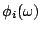稀奇的是(在謝氏原論文中，他亦稱奇)。只要這三個原則，即可求出 $\phi_i(\omega)$ 。

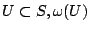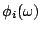定理（Shapley）：根據上項三原則，若對所有 $U\subset S,\omega(U)$ 已給定，則 $\phi_i(\omega)$ 的唯一解為

$\begin{displaymath} \phi_i (\omega) = \sum_{ U \subseteq S} r_n (s) [\omega(U)-\omega(U-\{i\})] \eqno{(1)} \end{displaymath}$

s = U 所含之元素數目,
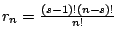
$r_n = \frac{(s-1)!(n-s)!}{n!}$
且 U-{i} 表示 U 中減去成員 {i}。

雖然本定理的證明不長(大約二頁，高中代數程度)，我們不在此重複，有興趣的讀者一定可以從本文的參考資料中找到。而且下文中會對(1)式做直觀的分析，即使不查證明，多數人也會相信(1)是一個公平的分配方式。為了明瞭此公式的用法，讓我們演算一下廠主的報酬，令

S={1,2,3,4}

1,2,3,4 依次代表廠主，工程師，工人甲乙。U 是 S 的子集合，共有 2⁴=16 個。可細列如下：

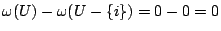(1) 空集合及含有一個元素的集合均使 $\omega(U)-\omega(U-\{i\})=0-0=0$ 。

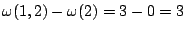(2)含有二個元素的集合有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)。其中只有 $\omega(1,2)-\omega(2)=3-0=3$ ，其餘均為0，而

$\begin{displaymath} r_2=\frac{(2-1)!(4-2)!}{4!}=\frac{1}{12}\mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 1}} \end{displaymath}$

(3)含有三個元素的集合有(1,2,3),(1,2,4),(1,3,4),(2,3,4)，其中

$\begin{eqnarray*} && \omega(1,2,3) - \omega(2,3)=6-0=6,\\ && \omega(1,2,4) - \o... ...a(1,3,4) - \omega(3,4)=0,\\ && \omega(2,3,4) - \omega(2,3,4)=0, \end{eqnarray*}$

且

$\begin{displaymath} r_3=\frac{(3-1)!(4-3)!}{4!}=\frac{1}{12} \end{displaymath}$

(4)含有四個元素的集只有(1,2,3,4)得

$\begin{displaymath} \omega(1,2,3,4)-\omega(2,3,4) =9-0=9,\mbox{ {\fontfamily{cwM0}\fontseries{m}\selectfont \char 47}}r_4=\frac{1}{4} \; . \end{displaymath}$

因此求得

$\begin{eqnarray*} \phi_{1}(\omega) &=& \frac{1}{12} \times 3 + \frac{1}{12} \times (6+6) + \frac{1}{4} \times 9 \\ &=& 3.5 \end{eqnarray*}$

同理可得

$\begin{eqnarray*} \phi_2(\omega) &=& 3.5 \\ \phi_3(\omega) &=& \phi_4(\omega)=1 \; . \end{eqnarray*}$

現在如果誰要再說這種分配不公平就為時已晚了，因為一旦你承認了謝卜勒三原則，則剩下的推導全是推不倒，像 a+b=b+a 之類的數學公理。而謝卜勒原則似乎又無懈可擊。因此我們不得不承認這個 3.5:3.5:1:1 是一個公平的分配法。

從另一個角度來看(1)式，我們發現

$\begin{displaymath} \omega(U)-\omega(U-\{i\}) \end{displaymath}$

表示的是 {i} 加入 U 時所增加的(邊際)利潤，也就是 {i} 所帶給 U 的利潤。而 r_n(s) 表示在所有 1,2,…,n 排列中，{i} 在 s 位置而能保持前後成員不變的或然率，因 s 是 U 所含的元素數目，也就是 {i} 成為 U 中最後加入成員的或然率。因此(1)所表示的是 {i} 成員為 S 團體帶來邊際利潤的期望值，這自然應是 {i} 所得到的報酬。好像不容易說得清楚，且看一個例子。因前例 4!=24 太大了一點，我們在前例中減少一個工人，看看(1)的分配是什麼回事。同時也可以比較一下少一個工人時對各人收入的影響。現在 S={1,2,3} 依次代表了廠主、工程師，及工人甲。表一的左邊有這三個數的全部排列法。其第二，三，四列代表的是在這種排列下，各人所帶的邊際利潤。以第一行的排列 1 2 3 為例。廠主先到，他不能開工，因此他帶來的利潤是 0，工程師第二個到，他與廠主合作可得 3 萬利潤，因此他帶來的邊際利潤是 3(不全是他的功勞，但算他帶來的)，工人最後來，他又帶來了 3 萬利潤因此這 3 萬就記在工人名下，因此在第一行中各人所帶來的利潤是 0,3,3，但我們沒有理由讓廠主先到，這 3! 的排列應有同等的機會(很公平是不是？)因此一平均下來，各人所帶來的利潤，也就是他們應有的報酬是 2.5,2.5,1。表一的最後三列是代表此表與(1)式的關係，只要仔細對照一下，就可以看出(1)所表示的就是這些排列下所產生的平均值。

排列	1	2	3	含1的 U	s	$\gamma_n(s)$
123	0	3	3	{1}
132	0	6	0	{1}	1	2/6
213	3	0	3	{2,1}	2	1/6
312	0	6	0	{3,1}	2	1/6
231	6	0	0	{1,2,3}
321	6	0	0	{1,2,3}	3	2/6
和	15	15	6			1
平均 (和/6)	2.5	2.5	1

表一：對 {i} 而言的邊際利潤

若把表一的結果與先前有二個工人的結果比較，我們會發現多來的工人乙與原先的工人甲同工同酬(很合理，是不是？)，都得了一萬元的報酬，但他所造成的另外二萬利潤則又被廠與工程師吞去了 (您覺得工人很倒霉是不是？還有更倒霉的事情在後面，如果真的要公平的話。) 因此無論由三原則推導，或由(1)式直觀，我們發現公平的分配並不像我們想像的那麼難纏。謝卜勒能看到這一點已造成他成為一代宗師的地位，他的公式已成為數理經濟學的柱石。

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：王弘倫 ∕ 校對：陳文是

最後修改日期：4/26/2002