| |
- ...1
- Pascal是數學史上所謂的天才數學家之一。據他的姊姊 Madam Perier 的回憶, Pascal在十二歲左右,他的父親要他先學會拉丁文和希臘文,然後再學數學,因此他們家中所有的數學書都被藏起來。小 Pascal 不管這一套,他自己導出一套平面幾何的定理,證明三角形的內角和是
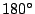 。Pascal著名的貢獻有,Pascal 三角形,圓錐曲線內接六邊形的 Pascal 定理。 。Pascal著名的貢獻有,Pascal 三角形,圓錐曲線內接六邊形的 Pascal 定理。
- ...2
- Leopold Kronecker(1823-1891)這句話的用意是,只有整數的概念是精確而不容置疑的,其他的數學概念,如有理數、實數,都應該建立在整數的基礎上。因此把2π定義成半徑為1的圓週的長度,不如定義
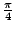 是1 是1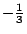 + +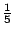 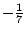 +…。Kronecker是當時柏林大學的教授,他的主要貢獻是,代數數論,橢圓函數,理想論,二次型理論。 +…。Kronecker是當時柏林大學的教授,他的主要貢獻是,代數數論,橢圓函數,理想論,二次型理論。
- ...3
- 古希臘幾何作圖三大難題是,只運用(沒有刻劃的)直尺與圓規,
- (1) 三等分任何已知角(三等分角問題);
- (2) 作一圓其面積等於任意給定的正方形面積(方圓問題);
- (3) 作一正立方體其體積為任意給定的正立方體體積的2倍(倍立方問題)。
這三個問題直到十九世紀才證明是無解的。由於方圓問題的解決,數學家更進一步研究超越數的各種性質,這就是Hilbert第七問題的背景,其結果是今日理論完美,成果豐碩的超越數理論(the theory of transcendental numbers)。
- ...4
- 文藝復興時代的義大利數學家已經知道三次方程式與四次方程式的根的公式。如何求得五次方程式的根的公式,或者更一般的,何種方程式的根可以由其係數作加減乘除開方求得呢?這個問題是由 Galois 完全解決。Galois 在二十一歲時死於決鬥。臨死前把他的結果寫成草稿。他死後將近三十多年,數學家才完全瞭解他的偉大貢獻。
- ...5
- 這句話引自德國數學家 Georg Cantor(1845-1918)。Cantor 是集合論(set theory)的創始者。集合論剛出現時,引起數學界極大的騷動。許多有名的數學家,如 L. Kronecker、F. Klein、H. Poincaré 都反對它,H. Weyl 甚至說,那是一團濃霧中的一團濃霧。不過也有許多人,如 A. Hurwitz、J. Hadamard、D. Hilbert、B. Russell,極力推崇集合論。Cantor 面對 Kronecker 這麼強硬的反對者,終於精神崩潰,最後在療養院渡其餘生。
- ...6
- Richard Dedekind(1831-1916)在德國Brunswick的專科學校教了三十一年的書。切割是 Dedekind 定義實數的方法。Dedekind 在數學上的貢獻主要在實數系的建造和代數數論。許多抽象代數的基本概念在 Dedekind 的論文中都可找到其原始形式(prototype)。二十世紀二十年代抽象代數的大師 Emmy Noether(1882-1935)有一句口頭禪:「Dedekind 如是說,……」。
|
|
|
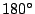 。Pascal著名的貢獻有,Pascal 三角形,圓錐曲線內接六邊形的 Pascal 定理。
。Pascal著名的貢獻有,Pascal 三角形,圓錐曲線內接六邊形的 Pascal 定理。
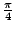 是1
是1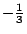 +
+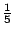
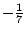 +…。Kronecker是當時柏林大學的教授,他的主要貢獻是,代數數論,橢圓函數,理想論,二次型理論。
+…。Kronecker是當時柏林大學的教授,他的主要貢獻是,代數數論,橢圓函數,理想論,二次型理論。