上頁　1│2│3　已在最後一頁

機率名題二則漫談 （第 3 頁）

戴久永

 

首頁 | 搜尋

．原載於數學傳播第四卷第四期
．作者當時任教於交大運輸工程與管理學系

•註釋
•對外搜尋關鍵字
 
解答

1、 ${5\choose 2}=10$。
2、 我們無法得知你選那一個順序，然而我們能保證你的圓圈必然與下列二者之一相合。 你所列出的順序應與以上二者之一相合。
3、 「甲一路領先」在圈I為甲甲甲乙乙，圈II為甲甲乙甲乙。
4、5、 你的第2題解答並未包含所有的順序。例如，倘若你的第2的解答如圓圈I所示，則第4題的解答如圓圈II所示。
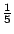6、 $P(\mbox{{\fontfamily{cwM2}\fontseries{m}\selectfont \char 248}\hskip 0.0pt plus... ...fontfamily{cwM0}\fontseries{m}\selectfont \char 108}})=\frac{2}{10}=\frac{1}{5}$（在所有個可能順序中，每個均為相等可能，其中有兩個「甲一路領先」，即甲一路領先的機率為 $\frac{1}{5}$）。
7、1。
8、是的， $\frac{(5-0)}{(5+0)}=1$。
9、是的。 $P(\mbox{{\fontfamily{cwM7}\fontseries{m}\selectfont \char 66}\hskip 0.0pt plus0... ...ily{cwM0}\fontseries{m}\selectfont \char 108}})=\frac{(2-1)}{(2+1)}=\frac{1}{3}$。
10、我們不清楚在你的圖上14甲和11乙如何安排，然而，我們肯定在你的試驗中，必然會有3個甲一路領先的順序，即 $\frac{(14-11)}{(14+11)}=\frac{3}{25}$。
11、 $\frac{(7-3)}{(7+3)}=\frac{2}{5}$。
12、 在1、3、6或7。
13、 1,4,9
14、 始於4、5、6或1。
15、 ${6\choose 2}=15$。
16、 你的圓圈依適當選取啟始點必然與以下圖形相合。

參考資料
1. F. Mosteller,《Fifty challenging problem in probability with solutions》, Addison Wesley Reading, Mass.
2. J.E. Nymann,〈Another generalization of birthday problem〉, Mathematics magazine 48 (1975), pp.46-47.
3. S. Goldberg, 〈A direct attack on a birthday problem〉, Mathematics magazine 49 (1976) pp. 130-131.
4. J. Kemeny, J. Snell,《Finite Mathematics with Business Applications》, 1966 Prentice Hall N.J.
5. 《機率挑戰名題展》，戴久永編著，協進圖書公司。

   

上頁　1│2│3　已在最後一頁

 回頁首
 
（若有指正、疑問……，可以在此 留言 或 寫信 給我們。）
EpisteMath

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有


編輯：黃信元 最後修改日期：4/26/2002