| |
用來玩拈的道具不限於銅板。工餘之時,石頭可以玩;無聊磕瓜子時,瓜子可以玩;圍棋子可以玩……。
也可以將石頭分堆放置,一堆相當於一列。這些都不是重點,我們甚至可以改變取銅板的規定,最後取光時輸贏的規定……,於是,各種不同的變型遊戲遂產生。
在拈的遊戲中,如果只有兩列銅板,則很容易看出來,留下兩列枚數相同的銅板是致勝的安全殘局。也就是我們一開始說的對稱這個想法。
事實上,包頓很巧妙的將對稱化成二進位和的各個位數為偶數,將問題給一般化,這是很天才的想法。所以兩列的拈是沒有什麼可說的。
將拈的規定略加修改,成為只有兩列的威氏遊戲,卻極其有意思。規定是這樣的,銅板只有兩列,
每列的枚數隨玩者任意規定,兩人輪流取銅板,取的時候,需要任一列中取一枚或多枚銅板,或者同時在兩列取同樣枚數的銅板,
直到最後將銅板取光的人贏。當然也可以像拈一樣有相反的規定,最後將銅板取光的人輸。今只討論前者。
拈的玩法完全不能適用於威氏遊戲。所有拈的安全殘局 {n,n},在威氏遊戲中都是不安全殘局。因為我們加了一個規定,可以從兩列銅板中同時取相同枚數的銅板。
- [例3]
若 n 是正整數,則 {0,n} 和 {n,n} 都是不安全殘局。
- [例4]
{1,2} 是安全殘局。因為
不管如何取,總是成為不安全殘局。
- [例5]
{3,5} 是安全殘局。
因為
不管對方如何取,不是到達例 3 的不安全殘局,就是你可以再適當取,使成例 4 的安全殘局。
繼續推演下去,可以得到許多組安全殘局 {1,2},{3,5},{4,7},{6,10},…。一般而言,第 n 組安全殘局 {an,bn} 可由下式定義得到
- (1) a1=1,b1=2。
- (2) 若
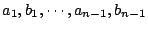 已經求得,則定義 an 為未出現在以上這 2n-2 個數中的最小整數。 已經求得,則定義 an 為未出現在以上這 2n-2 個數中的最小整數。
- (3) bn=an+n。
做成表就是
| n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| an |
1 |
3 |
4 |
6 |
8 |
9 |
11 |
12 |
14 |
16 |
| bn |
2 |
5 |
7 |
10 |
13 |
15 |
18 |
20 |
23 |
26 |
由(1)、(2)、(3)所定義的二數列
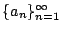 和 和
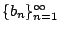 ,具有下列特性: ,具有下列特性:
- (甲)
數列
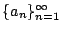 和 和
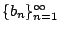 均是嚴格遞增數列,而且 bn=an+n。 均是嚴格遞增數列,而且 bn=an+n。
- (乙)
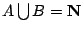 , ,
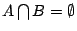 其中 N 表示正整數的集合, 其中 N 表示正整數的集合,
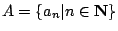 , ,
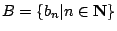
- (丙)
若
{an,bn}={am,bm},則 n=m,即
an=am, bn=bm。
事實上,相反的,具有(甲)、(乙)性質的數列,也就是具有(1)、(2)、(3)性質的數列。
- [定理]
{an,bn} 是威氏遊戲的安全殘局,其餘的組合 {x,y} 都是不安全殘局。
- [證]
我們只要證明下面二點即可。
- (1)由任何一組 {an,bn} 取銅板,不管如何取,都不會成為另一組 {am,bm}。
假設從一組 {an,bn} 中的 an 取 x,bn 取 y 而能達到另一組 {am,bm},則 an-x=am,bn-y=bm。
- (i) 當 x=0,y>0 時,an=am 則 n=m,得 y=0,矛盾。
- (ii) 當 x>0,y=0 時,bn=bm 則 n=m,得 x=0,矛盾。
- (iii) 當 x=y>0 時,
m=bm-am=(bm+y)-(am+x)=bn-an=n,矛盾。
- (2)由任一組不是 {an,bn} 型的 {x,y} 可以適當取銅板使成某一組 {am,bm}。為方便計,可假設
 。 。
- (i)當 x 為某個 bm 時,
y-am=y-(bm-m)=(y-x)+m>0,可在 y 中取 y-am,變成 {bm,am}。
- (ii)當 x 為某個 am,且 y>bm 時,在 y 中取 y-bm,變成 {am,bm}。
- (iii)當 x 為某個 am,且
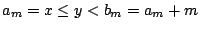 時,y-x<m,令 k=y-x,則
y-bk=x+k-(ak+k)=x-ak>0。在 x 中取x-ak,在 y 中取 y-bk=x-ak 則變成 {ak,bk}。 時,y-x<m,令 k=y-x,則
y-bk=x+k-(ak+k)=x-ak>0。在 x 中取x-ak,在 y 中取 y-bk=x-ak 則變成 {ak,bk}。
這個定理不但告訴我們 {an,bn} 是威氏遊戲的安全殘局,其證明過程更暗含從不安全殘局取銅板變成安全殘局的法則。
我們只要記住這個法則,還有 {an,bn} 組合,則無不處於優勢。但是有一個問題是,當數目很大的時候,要記住一大堆 {an,bn} 是一件非常吃力不討好的工作。我們於是自然會問,有沒有像拈類似的法則用來判斷任何一組 {x,y} 是否為威氏遊戲的安全殘局,
而不必逐一計算 {a1,b1},{a2,b2} …。答案是有的,在解答這之前,我們需要談談費氏數列及相關的問題。
|
|
|