投幣打賭與大數法則 (第 2 頁)

　1│2│3　

投幣打賭與大數法則（第 2 頁）

姚景星;林聰勤

首頁 | 搜尋

．原載於數學傳播第一卷第一期
．作者當時任教於台大數學系;台北市市立中正高中

‧註釋
‧對外搜尋關鍵字

二、利用大數法則推測硬幣出現的機率

某些機率的概念就實際應用來講，它是有某種程度上的人為。一個硬幣本來並無所謂出現正面的機率或反面的機率這種問題，但當我們把它拿來做為賭博工具的時候，為了要預測結局的得失，我們就提出機率這個概念來認識、分析投擲硬幣的這件事，（就像物理上，我們利用速度、加速度等概念來探討各種質點的運動），這種探討的過程，通常是一種逼近的過程，但所獲得的一些知識往往足以作為估計及策劃上的依據。

一個硬幣出現正面的機率 p 是一個在 0 與 1 之間的某一未知實數。在這裏用來打賭的這個硬幣，我們無法平白得知 p 是多少？現在我們藉用機率上的一些理論來說明如何可以合理地推測 p 值。為了討論上的方便起見，我們導入隨機變數 X。設出現正面時 X=1，其機率表為 p=P(X=1)，反面時 X=0，其機率 q=P(X=0)=1-p，則 X 的期望值為

$\begin{displaymath} E(X)=0\cdot P(X=0)+1\cdot P(X=1)=p , \end{displaymath}$

因

$\begin{displaymath} E(X^2)=0^2\cdot P(X=0)+1^2\cdot P(X=1)=p , \end{displaymath}$

故 X 的方差 ^註1 為

Var(X)=E(X²)-[E(X)]²=p-p²=p(1-p) ,

現在把這個硬幣獨立投擲 n 次，設隨機變數 X_i 表示投第 i 次出現的結果，出現正面時 X_i=1，反面時 X_i=0，顯然的P(X_i=0)=p,P(X_i=0)=1-p, i=1,2,…,n。而 E(X_i)=P, Var(X_i)=p(1-p), i=1,2,…,n。

上述的隨機變數 X₁,X₂,…,X_n 可如下證明它們是獨立隨機變數：由乘法定理，得

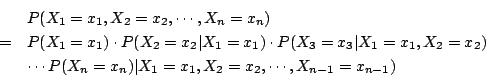
$\begin{eqnarray*} &&P(X_1=x_1,X_2=x_2,\cdots,X_n=x_n)\\ &=&P(X_1=x_1)\cdot P(X_... ...&&\cdots P(X_n=x_n)\vert X_1=x_1,X_2=x_2,\cdots,X_{n-1}=x_{n-1}) \end{eqnarray*}$

在這裏，x_i=0 或 1, i=1,2,…,n。

因對各 $m \in \mathbf{N}$ ， $2\leq m\leq n$ ，條件機率 $P(X_m=x_m)\vert X_1=x_1,X_2=x_2,\cdots,X_{m-1}=x_{m-1})$ 第2次，……，第 m-1 次的投出結果各出現 X₁=x₁，X₂=x₂，…， X_m-1=x_m-1 的條件下，第 m 次出現 X_m=x_m 的機率，但每次都是獨立投出，故第 m 次出現的結果和前面各次出現的結果無關，即

$\begin{displaymath} P(X_m=x_m\vert X_1=x_1,X_2=x_2,\cdots,X_{m-1}=x_{m-1})=P(X_m=x_m) \end{displaymath}$

於是

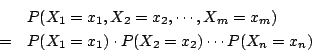
$\begin{eqnarray*} &&P(X_1=x_1,X_2=x_2,\cdots,X_m=x_m)\\ &=&P(X_1=x_1)\cdot P(X_2=x_2)\cdots P(X_n=x_n) \end{eqnarray*}$

此由定義得知 X₁,X₂,…,X_n 為獨立隨機變數。

再設另一隨機變數 $\overline{X}=\frac{1}{n}\sum_{i=1}^nX_i$ ，因 X_i 表示 0 或 1，故 $\sum_{i=1}^nX_i$ 為 n 次中出現正面的次數和 k，所以，隨機變數 $\overline{X}=\frac{1}{n}\sum_{i=1}^nX_i$ 表示 n 次中，正面的出現率 $\frac{k}{n}$ ，因 X₁,X₂,…,X_n 獨立，故由公式可得

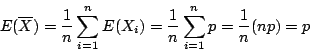
$\begin{displaymath} E(\overline{X})=\frac{1}{n}\sum_{i=1}^nE(X_i)=\frac{1}{n}\sum_{i=1}^np=\frac{1}{n}(np)=p \end{displaymath}$

$\begin{eqnarray*} Var(\overline{X})&=&\frac{1}{n^2}\sum_{i=1}^nVar(X_i)\\ &=&\f... ...\sum_{i=1}^nP(p-1)=\frac{1}{n^2}[np(1-p)]\\ &=&\frac{p(1-p)}{n} \end{eqnarray*}$

現在由柴比雪夫不等式可得：對任意 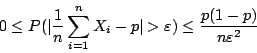$\varepsilon>0$ ，

$\begin{displaymath} 0\leq P(\vert\overline{X}-E(\overline{X})\vert>\varepsilon)\leq \frac{Var(\overline{X})}{\varepsilon^2}, \end{displaymath}$

也就是

$\begin{displaymath} 0\leq P(\vert\frac{1}{n}\sum_{i=1}^nX_i-p\vert>\varepsilon)\leq\frac{p(1-p)}{n\varepsilon^2} \end{displaymath}$

因當 $n\rightarrow\infty$ 時， $\frac{p(1-p)}{n\varepsilon^2} \rightarrow 0$ ，故

$\begin{displaymath} \lim_{n\rightarrow\infty}P(\vert\overline{X}-E(\overline{X})\vert>\varepsilon)=0 \; , \end{displaymath}$

這表示當 $n\rightarrow\infty$ 時， $\overline{X} = \frac{1}{n}\sum_{n=1}^n X_i$ 取值在區間 $[p+\varepsilon,p-\varepsilon]$ 中的機率趨近於 1。也就是說，如果投硬幣 n 次中出現正面的次數為 k，則當 n 很大很大時，絕大部分的情形都是

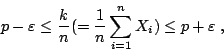
$\begin{displaymath} p-\varepsilon\leq\frac{k}{n}(=\frac{1}{n}\sum_{i=1}^nX_i)\leq p+\varepsilon \; , \end{displaymath}$

故 n 很大很大時， $\frac{k}{n}\doteq p$ ，這就是所謂的大數法則。它的意義可解釋如下：

: 對於任意小的定數 $\varepsilon>0$ ，我們可選定足夠的 N，使得 $P(p-\varepsilon \leq \frac{1}{N} \sum_{i=1}^N X_i \leq p+\varepsilon)$ 的值接近於 1。

假設每獨立投擲 N 次就當作一回合。現在先獨立投擲 N 次做為第一回合，設每次的結果依次表為 X₁⁽¹⁾,X₂⁽¹⁾,…,X_N⁽¹⁾（注意：當第 i 次出現正面時 X_i⁽¹⁾ = 1，反面時 X_i⁽¹⁾ = 0，以下同樣意義），則可得第一回合正面的出現率 $\overline{X^{(1)}} = \frac{1}{N}\sum_{i=1}^N X_i^{(1)}$ 。再重新獨立投擲 N 當作第 2 回合，可得另一組結果，設為 X₁⁽²⁾,X₂⁽²⁾,…,X_N⁽²⁾，則第二回合的正面出現率 $\overline{X^{(2)}} = \frac{1}{N} \sum_{i=1}^N X_i^{(2)}$ ，（ $\overline{X^{(1)}}$ 不一定等於 $\overline{X^{(2)}}$ ），這樣重複同樣的試驗 m 回合可得：

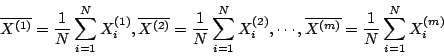
$\begin{displaymath} \overline{X^{(1)}}=\frac{1}{N}\sum_{i=1}^NX_i^{(1)},\overlin... ...2)},\cdots,\overline{X^{(m)}}=\frac{1}{N}\sum_{i=1}^NX_i^{(m)} \end{displaymath}$

在圖一所示的 $n-\overline{x}$ 座標圖上，

圖一

我們將 m 個點

$\begin{displaymath} Q_1(N,\overline{x^{(1)}}),Q_2(N,\overline{x^{(2)}}),\cdots,Q_m(N,\overline{x^{(m)}}) \end{displaymath}$

描在 n=N 的直線上時，由上述的大數法則得知這些點絕大多數都會落在 L₁ 和 L₂ 兩直線之間（如圖 l）。這就是說，在 m 回合中，幾乎每一回合的正面出現率 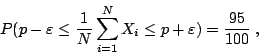$\overline{x}(=\frac{k}{N})$ 都介於 $p-\varepsilon$ ，和 $p+\varepsilon$ 之間。為了更明白起見，我們舉個實值的例子來說明。設

$\begin{displaymath} P(p-\varepsilon\leq\frac{1}{N}\sum_{i=1}^NX_i\leq p+\varepsilon) = \frac{95}{100} \; , \end{displaymath}$

則大約可說平均 100 個 $Q(N,\overline{x})$ 點中，只有 5 個會落在 L₁ 和 L₂ 所夾的帶域之外。因此我們實驗時，只要 N 足夠大，則把投 N 次後所得的正面出現率 $\overline{x} = \frac{1}{N} \sum_{i=1}^N x_i$ 當作 p 值是很可靠的，這就是大數法則的應用。

　1│2│3　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：黃信元

最後修改日期：4/26/2002