|
在許多問題中，我們需要解函數 f(x) 的根，例如要瞭解函數的特徵，必須求三個方程式的根：f(x) = 0（根），f'(x) = 0（起伏極值），f''(x) = 0（凹性、反曲點）。當然，我們曾經學過一些多項式的求根公式，但是在大部分的情況，數學家也沒有辦法給出公式，例如數學家已經證明超過4次的多項式就沒有一般的公式解，更不用說像 ex - x = 0 這類方程式的根了。而且就算能解出多項式函數的根，這些解經常帶著許多根號（例如
![$\sqrt{\frac{1 + \sqrt[3]{5}}{2}}$](img1.gif) ）。在應用上，這只是符號，它的用處往往還不如實實在在用小數表示的近似值。因此，如何給出一個方程式的數值解，便是一個重要課題。牛頓勘根法，即是我們在求數值近似解時，常用的一個方法。
這裡將藉由實際操作 java applet，來觀察牛頓勘根法的操作行為。
-
牛頓勘根法的操作步驟：
- (1)
- 找一個起點 x0。
- (2)
- 從 (x0,f(x0)) 作切線
y = f'(x0)(x - x0) + f(x0) 交 x-軸於
- (3)
- 續用此法，得到數列 xn 的遞迴關係式：
首先看一個簡單的例子：
-
- 例 1.
- 利用牛頓勘根法來求
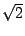 。此亦即求
f(x) = x2 - 2 = 0 的正根。你可以先取 x0 = 2 計算。然後再試試其他的 x0 值。
假如取 x0 = 0 有何結果？為什麼？
再看另一個例子：
-
- 例 2.
-
f(x) = 2x5 - 10x3 + 8x + 1，令 x0 = 2，用牛頓戡根法求出一根。若換成 x0 = 1 呢？
由此例可以發現：不同的起始點收斂到不同的根；而且，收斂的速度非常快。
然後我們再進一步觀察這個例子：
-
- 例 3.
- （續上例）觀察 x0 = 0.46887 的變化行為。（放大率：x 軸取100、y 軸取15）
在上面的例子裡，你觀察到哪些奇怪的行為？你能否預測還有哪些別的奇怪行為？由此我們可以看出，牛頓法並非萬能。
 |
EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有
|
| 
