.原載於科學月刊第十七卷第三期
.作者當時任教於台大數學系
曹亮吉
|
.原載於科學月刊第十七卷第三期 .作者當時任教於台大數學系 | |||
|
萊布尼茲的微積分
曹亮吉 |
|
我們談過了牛頓如何突破微積分(參閱〈牛頓如何突破微積分學〉),現在再來看對微積分一樣有決定性貢獻的萊布尼茲,他的微積分又是什麼樣子。 萊布尼茲(Gottfried Wilhelm Leibniz, 1646∼1716年)生於來比錫,早歲聰慧,十五歲就進來比錫大學,十七歲畢業,二十一歲(1667年)又從紐倫堡的 Altdorf 大學得到博士學位。學生時代的萊布尼茲主要的興趣在於邏輯、哲學與法律。 畢業後,萊布尼茲進入 Mainz 大選侯的政府。1672年到1676年這段時間,他因外交任務的關係滯留在巴黎,也就在這段時間內,他遇到著名的物理學家 Huygens(Christiaan, 1629∼1695年),引起了他對數學的興趣,而投入微積分學的創造,1676年萊布尼茲回到德國,安頓了下來,成為 Hanover 大選侯的顧問及圖書館主管。
雖然萊布尼茲在巴黎時就得到很多微積分的結果,他在這方面第一篇重要的著作〈求極大小值及切線的新方法〉,卻要到1684年才發表在來比錫的一份雜誌《Acta Eruditorum》上。在這篇文章中,他引進了微分式,給了微分式的四則公式:
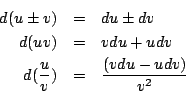
並說明得到極值的條件是 dv=0,得到迴轉點(反曲點)的條件是 ddv=0。 在此之前,微分的計算都是個案的;有了萊布尼茲的微分公式,則只要知道簡單函數的微分,其他由簡單函數經四則運算合成的複雜函數,其微分也就輕易算得,難怪萊布尼茲會為此新方法感到興奮不已。
第二年(1685年),牛頓的一個學生 Craig(John, 1660?∼1731年)寫了一本數學書,提到萊布尼茲的微分學,認為一定有更多的結果還未發表。再過一年(1686年),萊布尼茲在《Acta Eruditorum》發表了〈論一深度隱藏的幾何學及無窮小與無窮大的分析〉一文,為 Graig 的書做書評,並趁機推出更多的萊氏微積分,在這篇文章中,萊氏積分符號
萊布尼茲的想法是這樣的:在 P 點無窮小鄰近取曲線上一點 Q,以 PQ 為「斜邊」做一「特徵(直角)三角形」 此外,在這篇文章中,他還說圓弧之長及擺線等非代數函數都可用積分的方式表示出來。
在積分的技巧方面,萊布尼茲是以善用特徵三角形出名的。特徵三角形的想法可溯至Pscal(Blaise, 1623∼1662年)處理圓球表面積的工作。如圖二,在半徑為 r 的圓上,取鄰近的兩個點 P、Q。
因特徵三角形 就是圓球的表面積。
萊布尼茲在巴黎時,Huygens 介紹他讀 Pascal 的文章;萊氏在研讀 Pascal 的這段證明時,突然靈光一閃,發現在一般曲線的場合,法線代替了半徑,也可以算得旋轉體的體積:如圖一所示。從兩個三角形的相似,我們也可以得到 yds = ndx,因此
這兩個三角形相似的另一用法就是(1)式。由於
所以為了求得一函數 v(x) 的積分,我們只要找到 y=f(x),使得(3)式成立就好了。譬如,v(x)=xn 時,我們可以試 f(x)=bxm。則因
所以取 (3)式與(1)式合起來看,我們就得 這正是積分中變數代換的一個例子。
特徵三角形還可以和其他的三角形相似。譬如在圖三中,PT 為切線,AB 為高度固定為 a。由 因此,譬如說,我們可以得到 而把計算弧長的問題轉變為計算面積的問題。
然而下面這種相似三角形取法更有用。如圖四,設切線交 y 軸於 Z(o,z),
從 O 到切線的垂足為 H,垂線 OH 長為 h。從 因此由 就得 因為 把其中的 y 做一次分部積分 (integration by parts),(6)式就變成 這正是我們常見的分部積分公式。
(6)、(7)兩式的合用是萊布尼茲計算積分的主要方法。他宣稱由此可以得到所有前人已知的積分;圓周率的計算是這種方法成功的例證。如圖五,圓的方程式為
由此可得 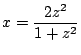 ,因此 ,因此
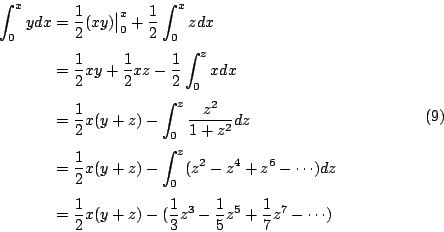
取 x=1,就得以萊布尼茲為名的著名公式 若將(9)式重寫成 而且注意到 z ( 如此我們就得到反正切函數的展開式
[請注意:牛頓與萊布尼茲得到 tan-1 z 的展開式都不是先知道其微分為
在牛頓、萊布尼茲之前,微分及積分的計算都是個案的。萊氏不但提供了微分的方法,也提供了積分的方法,而積分的公式,實際上都是利用特徵三角形所得的「微分」方程式轉過來的;也就是說他體會到求積的問題可從曲線的切線性質著手,而且也善於應用微積分基本定理──他曾於1693年在《Acta Eruditorum》發表微積分基本定理。此外他的微積分符號不但使人很快了解微積分的內涵,也使人在微積分的計算上得心應手,因此萊布尼茲的微積分掩蓋了牛頓的,而成為日後微積分學的主流。有了這些貢獻,萊布尼茲自然也成了微積分的創始人之一。
|
對外搜尋關鍵字: .牛頓 .萊布尼茲 .微分式 .極值 .反曲點 .微分 .旋轉體 .變數代換 .微積分基本定理 |
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:朱安強 / 繪圖:簡立欣 | 最後修改日期:5/31/2002 |