.原載於科學月刊第十六卷第七期
.作者當時任教於台大數學系
曹亮吉
|
.原載於科學月刊第十六卷第七期 .作者當時任教於台大數學系 | |||
|
Poisson 分布
曹亮吉 |
|
二項分布是離散型機率模型中最有名的一個,其次是 Poisson 分布,它可以看成為二項分布的一種極限情形。
假定某機關的總機在一個短時間
我們可以把 t 分成 n 小段,每小段長為
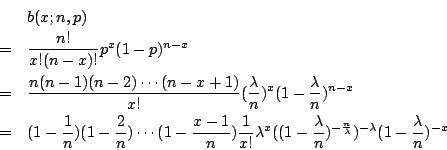
當 t 保持不變(亦即 λ 不變),而讓 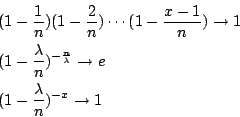
所以
因為
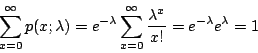
所以
這就是說,在時間 t 內,接到 x 次電話的機率為
Simeon D. Poisson(1781∼1840年)是一個著名的法國數學家及物理學家。到了晚年,他熱衷於將數學的機率論用到司法的運作上。他在這方面的主要著作是1837年出版的《司法機率的研究》(Recherches sur la Probabilité des Jugements)。雖然這本書的主旨是要對司法運作有具體的貢獻,但它包含了許多純粹數學的、機率的理論,所以可以看成是一本以司法應用為例的機率課本,這本書德文版的書名《機率論及其重要應用》(Lehrbuch der Wathrscheinlichkeitsrechnung und deren wichtigstein Auwendungen) 看起來和內容較為一致。在這本書的數學推演中,Poisson 從二項分布的極限得到了這個日後以他為名的機率分布。
Poisson 雖然得到這樣的機率分布,但在書中他並沒有繼續討論這種分布的性質,在往後的研究中,Poisson 似乎也把它忘掉了。
在十九世紀的許多統計研究報告上,Poisson 這個名字經常出現,但這與 Poisson 分布無關,大家所關注的是他在常態分布方面的研究。常態分布在解釋理論與數據變異之間的關係非常成功,當時許多人認為常態分布是機率與統計之間唯一的橋梁了。
直到十九世紀末,Bortkiewicz 才注意到 Poisson 分布與某些數據之間也有類似的關聯。Ladislaus von Bortkiewicz(1868∼1931年)是出生在俄國聖彼得堡的波蘭人。他在德國 Göttingen 大學得到學位(1893年),並曾在 Strassburg 做過研究。在 Strassburg 時,他寫了一本小冊子《小數法則》(Das Gesetz der Kleinen Zahlen),專門研究 Poisson 分布。他不但在理論方面推演了 Poisson 分布的許多性質,並且在應用方面,也比較了一些實際發生的、有關於自殺或意外傷害的數據。Poisson 分布雖然出於 Poisson 之手,但真正使它為人重視,使它成為統計學一部分的可要算是 Bortkiewicz了。
在這本書中,Bortkiewicz 舉了一個至今仍是膾炙人口的例子,說明數據契合 Poisson 分布的情形。從1875到1894年的20年間,德國的十四個軍團部有士兵被馬踢傷因而致死的人數紀錄。這 20×l4 = 280個(團年)紀錄,按死亡人數來分,則如表一的左二欄所示。
在280個紀錄中,死亡的人數共有196,因此致死率為
Poisson 分布既然是二項分布的極限情形,反過來 Poisson 分布也可以做為二項分布的近似值。譬如 p=0.04,n=49,則
我們發現對應的值相當接近。一般,若用列表方式,則二項分布 b(x;n,p) 要兼顧三個變數 x,n,p,而 Poisson 只要兩個:x,λ,所以較為方便。若直接計算,則因
b(x;49,0.04)=Cx49(0.04)x(0.96)49-x
所以二項分布算起來相當費事。另一方面
通常只要 n 很大,p 很小,
由表三可知售量達到 5 罐以上的機率只有 5.3%,而達到 6 罐以上則只有 1.7%。所以合理的庫存量為 4 罐(平均19星期才會有一次缺貨),如果怕萬一,那麼 5 罐就非常保險(平均59星期才會有一次缺貨)。
我們從另一個角度來看上面的數據。假設某工廠每做100個螺絲釘,平均會有兩個不合規格,而這是合理的不合格率。根據 Poisson 分布,偶而出現 3 個或 4 個不合規格的螺絲釘也是正常的現象。但是如果出現的頻率太高,或出現 5 個以上的不合規格的螺絲釘,那麼生產過程就可能出了問題。Poisson 分布是品質管制的利器,它可以幫助我們決定生產過程是否出了毛病。
Poisson 分布還有種種的用途:放射性物質的蛻變、細胞間因受 X 光照射而引起的染色體交換次數、細菌和血球的計數、交通事故數及死亡率等等莫不遵行 Poisson 分布。其實,無論在自然科學、在工業、在農業、在商業、在醫藥、在交通、在社會或在軍事上,無不可找到 Poisson 分布的應用。
和二項分布一樣,我們也可以從理論方面來探討 Poisson 分布的期望值 μ 及散布差 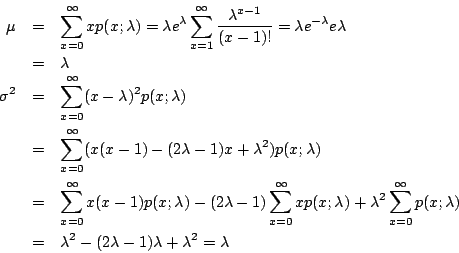
所以 Poisson 分布的確是以 λ 為期望值。
在〈二項分布與大數法則〉(《科學月刊》第十六卷第六期)一文中,我們曾導出二項分布的 Chebyshev 不等式
如果把二項分布換成 Poisson 分布或任何離散型分布,不等式也照樣成立,因為在導出不等式的過程中只用到 b(x;n,p) 是種機率分布這件事,並沒有用到 b(x;n,p) 之值。現在既然知道 Poisson 分布的 亦即:在 Poisson 分布的機率模型假定之下,只要試驗的次數 n 夠大,則事件發生的次數比
|
對外搜尋關鍵字: .Poisson .常態分布 .Chebyshev |
|
|
|
|
(若有指正、疑問……,可以在此 留言 或 寫信 給我們。) |
|
|
|
EpisteMath (c) 2000 中央研究院數學所、台大數學系 各網頁文章內容之著作權為原著作人所有 |
| 編輯:李渭天 | 最後修改日期:2/17/2002 |