二項分布與大數法則

．原載於科學月刊第十六卷第六期
．作者當時任教於台大數學系

‧註釋

二項分布與大數法則
理論與實際相連

曹亮吉

在〈藥效如何〉（《科學月刊》第十六卷第五期）一文裏，我們假設某藥的治療率為 0.6，然後算出 10 人中有 x 人痊癒的機率為 C¹⁰_x(0.6)^x(0.4)^10-x。這是一種機率分布；我們的目的是把試驗的結果拿來和此機率分布模型相對照，以決定治癒率為 0.6 的假說是否合理。

上面這種機率分布稱為二項分布。一般的二項分布是這樣的：假設某事件的發生率為 p，而試驗做了 n 次。則 n 次中，某事件發生 x 次的機率為

b(x;n,p)=C_xⁿp^x(1-p)^n-x

通常我們把 n、p 固定，讓 x 變動，以研究其機率變動的情形。這種機率分布之稱為二項分布。因為它可經由二項式 (p+(1-p))ⁿ 的展開式而得：

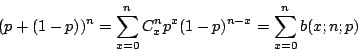
$\begin{displaymath} (p+(1-p))^n=\sum_{x=0}^{n}C_x^np^x(1-p)^{n-x}=\sum_{x=0}^n b(x;n;p) \end{displaymath}$

（上式的左邊等於 1；這正表示各種可能的 x 值，其發生的機率之和為 1。）因此有關二項分布的理論與計算和二項係數 C_xⁿ 的性質有密切的關係。

讓 x 變動，則 b(x;n,p) 變化的情形如何？我們以 n=10,p=0.6 為例，列成下表

x	b(x;10,0.6)	x	b(x;10,0.6)
0	0.0001	5	0.2007
1	0.0026	6	0.2508
2	0.0106	7	0.2150
3	0.0425	8	0.1209
4	0.1125	9	0.0060

我們發現 b(x;10,0.6) 之值隨著 x 之值逐漸升高，到了 x=6 時最大，然後又逐漸變小。這種現象毋寧說是預期的，因為 n=10，p=0.6，所以預期 x=np=6 最可能發生，而 x 離開 6 愈遠愈不可能發生。

一般的 n,p 也有類似的現象。直接從公式來看，我們可以這樣解釋： $x \leq 1$ 時

$\begin{displaymath} \frac{b(x;n,p)}{b(x-1;n,p)}=\frac{n-x+1}{x}\cdot\frac{p}{1-p} \end{displaymath}$

當 x 小的時候，這個比值會大於 1，而當 x 大過某種程度後，這個比值會小於 1，這只表示 b(x;n,p) 之值由小變大，然後再變小。什麼時候達到最大值？當上述比值由大於 1 變成小於等於 1 的時候。假設

$\begin{displaymath} \frac{n-x+1}{x}\cdot\frac{p}{1-p}>1\quad \mbox{{\fontfamily{... ...\char 55}}\quad\frac{n-(x+1)+1}{x+1}\cdot \frac{p}{1-p} \leq 1 \end{displaymath}$

則 np-x>-p 而 $np-x\leq 1-p$ 。兩式合併得 $1-p \geq np-x>-p$ 。因為 0<p<1，所以當 x 為兩個最接近 np 向的整數之一時（np 不一定是整數），b(x;n,p) 達到最大值。

我們可以從另一個觀點來看 np 這個值。由於我們有 b(x;n,p) 的機率得到 x 值，所以平均起來得到的 x 值應為

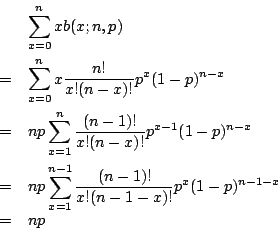
$\begin{eqnarray*} & &\sum_{x=0}^{n} xb(x;n,p)\\ &=&\sum_{x=0}^{n} x \frac{n!}{x... ...m_{x=1}^{n-1} \frac{(n-1)!}{x!(n-1-x)!}p^x(1-p)^{n-1-x}\\ &=&np \end{eqnarray*}$

$\mu=np$ 就稱為二項分布 b(x;n,p) 的期望值或平均值。

雖然 x 的期望值是 np，但這不就表示 x 值常出現在 μ 值附近。也許有很多 x 值比 μ 小得多，而正好有很多 x 值比 μ 大得多，兩相抵消，平均起來，x 值就在 μ 附近。為了估計 μ 與 p 差多少，又兼顧 x 值發生的機率，我們要引進方差 ^註1 $\sigma^2=\sum_{x=0}^n(x-\mu)^2 b(x;n,p)$ ，它要等於

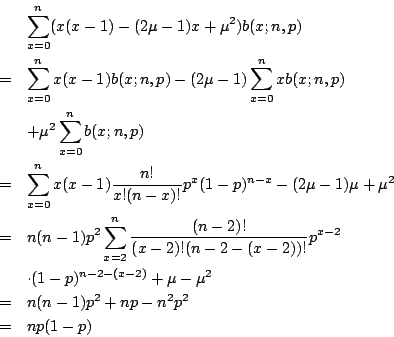
$\begin{eqnarray*} &&\sum_{x=0}^n(x(x-1)-(2\mu-1)x+\mu^2)b(x;n,p)\\ &=&\sum_{x=0... ...p)^{n-2-(x-2)}+\mu-\mu^2\\ &=&n(n-1)p^2+np-n^2p^2\\ &=&np(1-p) \end{eqnarray*}$

若 c 為正數，我們要估計有多大的機會， $\vert x-\mu\vert$ 會大於 c。由 σ 的定義，我們得

$\begin{eqnarray*} \sigma^2&=&\sum_{\vert x-\mu\vert>c}(x-\mu)^2b(x;n,p)+\sum_{\v... ...c}(x-\mu)^2b(x;n,p)\\ &>&c^2 \sum_{\vert x-\mu\vert>c} b(x;n,p) \end{eqnarray*}$

因此我們就得到 Chebyshev 不等式：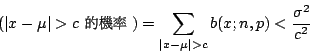

$\begin{displaymath} (\vert x-\mu\vert>c \mbox{ {\fontfamily{cwM1}\fontseries{m}\... ...}) = \sum_{\vert x-\mu\vert>c} b(x;n,p) < \frac{\sigma^2}{c^2} \end{displaymath}$

假設 $\epsilon$ 為正數，令 $c=n\epsilon$ ，則上式可改寫成

$\begin{displaymath} (\vert\frac{x}{n}-p\vert>\epsilon \; \mbox{{\fontfamily{cwM1... ...2} =\frac{np(1-p)}{n^2 \epsilon^2} =\frac{p(1-p)}{n\epsilon^2} \end{displaymath}$

因為上式的右邊也隨著 n 增大而趨近於 0，所以無論 $\epsilon$ 原來有多小，只要 n 夠大， $\frac{x}{n}$ 與 p 之差要大於 $\epsilon$ 的機率就會任意小，亦即

$\begin{displaymath} \lim_{n \longrightarrow \infty}(\vert\frac{x}{n}-p\vert> \ep... ...1pt{\fontfamily{cwM7}\fontseries{m}\selectfont \char 48}}) = 0 \end{displaymath}$

這就是所謂的大數法則：在二項分布的機率模型假定之下，只要實驗的次數 n 夠大，則事件發生的次數比 $\frac{x}{n}$ ，從機率的觀點來看，就會很接近 p 值。這是機率論萌芽初期的一個重要定理，它由 Jakob Bernoulli（1654～1705年）首先證得完整，而在他死後發表於1713年。可注意者，Chebyshev（1824～1894年）是十九世紀的數學家，生在 Bernoulli 之後，我們用他的不等式反推 Bernoulli 的大數法則是有違歷史順序的。不過 Chebyshev 不等式非常簡單，而且很容易推廣到其他的機率分布，正足以說明大數法則的基本所在。

二項分布 b(x;n,p) 的 p 是個非常重要，但不容易理解的概念。譬如我們說一個「公正」的骰子其出現 1 的機率為 $p\frac{1}{6}$ ，那是假定投擲「公正」的骰子時，1、2、3、4、5、6 出現的機會都一樣；反過來說，出現的機會一樣多，我們才說骰子是公正的。所以「公正」的骰子是理想的、數學式的產物，因為只有等待多次的投擲，才能確定某個骰子出現各數的機會是否都一樣。

又譬如說，某藥的治癒率是什麼呢？我們下能試完所有的人以決定 p 值，我們只能假定有個 p 值，使得藥效的數據遵行二項分布 b(x;n,p)。所以這個 p 值是抽象的、未知確值的假定值。

Bernoulli 的大數法則首先把這種基於定義、理想中的的數學產物 p 和實際的、實驗的結果 $\frac{x}{n}$ 相連起來；雖然大數法則並不保證長期實驗的比值 $\frac{x}{n}$ 一定會愈來愈靠近原先假定的機率 p，但至少保證這個比值靠近 p 值的機率，會隨著實驗次數增加而靠近 1。也就因為有此保證，我們常常以長期實驗所得的比值代替理想中的 p 值。我們說某藥的治癒率為 0.6，其所代表的意義正是如此。

二項分布的起源與賭博有密切的關係。當然二項分布的應用自不限於賭博，藥效的檢定、產品好壞的檢定等等莫不涉及。此外二項分布還可以導出其他的機率分布，著名的 Poisson 分布就是。這正是我們下次的話題。

對外搜尋關鍵字：
．二項分布
．Chebyshev不等式
．大數法則
．Jakob Bernoulli
．Chebyshev
．Poisson分布


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：朱安強

最後修改日期：2/17/2002