代數學基本定理

首頁 | 搜尋

．原載於科學月刊十六卷第一期
．作者當時任教於台大數學系

‧註釋

代數學基本定理

曹亮吉

附錄：另一種證法（高中生也能懂的）

狹義的代數學史可以說是一部解多項式方程式的歷史。解方程式的問題大約可以分成有沒有解、如何找解兩部分；代數學基本定理就是問題第一部份的一個重要答案，它說：一個多項式方程式一定會有一個複數根。

一次方程式當然有一個根，二次方程式 ax²+bx+c=0 當然有兩個根

$\begin{displaymath} x=\frac{-b \pm \sqrt{b^2-4ac}}{2a} \end{displaymath}$

這些事實很早就知道了；但是前人處理的是實數的問題，如果 b²-4ac<0，他們會說根居然含有虛數（負數的平方根），是荒謬的，該揚棄的。不過就二次方程式而言，什麼時候有（實數）解，如何求解都不成問題。

三次呢？三次（和四次）方程式的求解歷史雖然相當曲折有趣 ^註1 ，但我們想談的是它與虛數的關係。

一般的三次方程式都可以經由移根的處理而變成 x³+px+q=0。當你注意到

(u+v)³-3uv(u+v)-(u³+v³)=0

這樣的恆等式，就知道三次方程式的解法訣竅在那裏：令

$\begin{displaymath} u^3+v^3=-q,\quad uv=-\frac{p}{3} \end{displaymath}$

如果 u,v 有解，那麼 x=u+v 就是 x³+px+q=0 的解了。因為 u³,v³ 滿足，

$\begin{displaymath} u^3+v^3=-q,\quad u^3 v^3=-\frac{p}{27} \end{displaymath}$

所以它們滿足二次方程式 $y^2+qy-\frac{p^3}{27}=0$ ，由此解得

$\begin{displaymath} u^3,v^3=-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}} \end{displaymath}$

所以

$\begin{displaymath} \begin{eqalign} x&=u+v\\ &=\sqrt[3]{\frac{-q}{2}+\sqrt{\fr... ...ac{-q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}\\ \end{eqalign}\end{displaymath}$

(1)

這是所謂的 Cardano 公式。 Cardano（1501～1576年）以 x³+6x=20 為例，說明這種解法。因為

$\begin{displaymath} \frac{q^2}{4}+\frac{p^3}{27}=\frac{(-20)^2}{4}+\frac{6^3}{27}=108 \end{displaymath}$

所以

$\begin{displaymath} x=\sqrt[3]{10+\sqrt{108}}+\sqrt[3]{10-\sqrt{108}} \end{displaymath}$

可是當 Cardano 用同樣方法解 x³=15x+4 時，卻讓他嚇了一大跳：因為

$\begin{displaymath} \frac{q^2}{4}+\frac{p^3}{27}=\frac{(-4)^2}{4}+\frac{(-15)^2}{27}=-121 \end{displaymath}$

因此

$\begin{displaymath} x=\sqrt[3]{2+\sqrt{-121}}+\sqrt[3]{2-\sqrt{-121}} \end{displaymath}$

它含有負數的平方根，但 x=4 明明是一個解啊！

其實，由複數的計算可知

$\begin{displaymath} (2 \pm \sqrt{-1})^3=2 \pm 11\sqrt{-1}=2 \pm \sqrt{-121} \end{displaymath}$

所以 u、v 可取為 $2+\sqrt{-1}$ 及 $2-\sqrt{-1}$ ，而

$\begin{displaymath} x=(2+\sqrt{-1})+(2-\sqrt{-1})=4 \end{displaymath}$

正好是所要的答案。虛數居然可以幫助解決實根的問題，它除了荒謬外，又加上一層神秘的色彩。

將 x-4 這個因式從 x³-15x-4 除去後，得商 x²+4x+1。所以 x³=15x+4 還有 x²+4x+1=0 的兩個解 $x=-2 \pm \sqrt{3}$ 。然而它們在 Cardano 的解法中怎麼沒有出現？毛病在於把 $2+\sqrt{-121}$ 開三次方時，我們只取其中的一個根 $2+\sqrt{-1}$ 。如果以 w 表 1 的三次方根 $-1+\frac{\sqrt{-3}}{2}$ ，則 $2+\sqrt{-121}$ 的其他兩個三次方根為

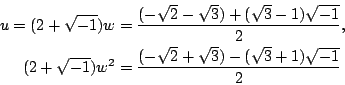
$\begin{eqnarray*} u=(2+\sqrt{-1})w &=&\frac{(-\sqrt{2}-\sqrt{3})+(\sqrt{3}-1)\sq... ...{-1})w^2 &=&\frac{(-\sqrt{2}+\sqrt{3})-(\sqrt{3}+1)\sqrt{-1}}{2} \end{eqnarray*}$

因為 $uv=-\frac{p}{3}$ ，所以相應的 v 值為

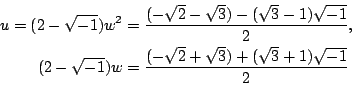
$\begin{eqnarray*} u=(2-\sqrt{-1})w^2 &=&\frac{(-\sqrt{2}-\sqrt{3})-(\sqrt{3}-1)\... ...rt{-1})w &=&\frac{(-\sqrt{2}+\sqrt{3})+(\sqrt{3}+1)\sqrt{-1}}{2} \end{eqnarray*}$

由此可得 $x=u+v=-2-\sqrt{3}$ 或 $-2+\sqrt{3}$ 。

從這個例子可知，除了(1)外，x³+px+q=0 的其他兩根為

$\begin{displaymath} \begin{eqalign} x&=\sqrt[3]{\frac{-q}{2}+\sqrt{\frac{q^2}{4}... ...c{-q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}} \;w \end{eqalign}\end{displaymath}$

(2)

由(1)(2)可知， $\frac{q^2}{4}+\frac{p^3}{27}\leq 0$ 時，方程式有三個實根，而當 $\frac{q^2}{4}+\frac{p^3}{27} > 0$ 時，方程式有一實根(1)及兩個共軛複根(2)。雖然一定有實根，在這些公式中虛數有如魔鬼附身，想將其揚棄都身不由己。

虛數在 Cardano 公式中出現後，大家又幾乎忘了它的存在。一直到1700年左右，在部分分式的積分中，虛數又重新出現，激起了數學家對虛數及其對數的辯論。雖然 Euler（1707～1783年）、d'Alembert（1717～1783年）、Lagrange（1736～1813年）等數學家使複數的使用有長足的進展，但十八世紀數學家的態度，卻可以用 Euler 的一段話來代表：

所有可能的數不是大於 0 就是小於 0 或等於 0，所以負數的平方根就不能是個數。既然是不可能的數，……，我們只能稱之為虛數，因為只有在虛幻中才會有這樣的數。

從來，在西方的數學中，數總是以幾何量的形態出現，而且要以幾何量的形態出現，才會令人安心，使人接受， $\sqrt{2}$ 或負數都是例子。虛數如果無法與幾何量連在一起，它在數學上總是像私生子一樣，無法有合法的地位。

使虛數合法化的努力，經過 Wallis、Kuhn、Buée、Argand 等人的嘗試，總算漸有眉目。到了十九世紀，數學家終於習於把一個複數 x+yi 與平面上的點 (x,y) 對應起來，虛數才完全為人所接受。

隨著虛數使用的日見活躍，任一多項方程式都會有（複數）根的信念就愈加增強。Euler、d'Alembert、Lagrange 等人都嘗試著去證明。直到 Gauss（1777～1855年）的出現，才使證明有長足的進步。1799年，Gauss 在 Helmstädt 大學的博士論文中，就將前人的證明的缺失一一指出，然後提出自己的見解。除了博士論文外，在1815年及1816年，他又分別提出另外兩種的證法。到了晚年（1849年）Gauss 又回到博士論文的方法，提出更完整的說明。

在博士論文中，Gauss 的想法是這樣的：假定 f(z) 是個複數 z=x+yi 的多項式，f(z) 是個複數，可以寫成為

f(z)=p(x,y)+q(x,y)i

p(x,y)、q(x,y) 都是實數，都是 x,y 的函數。求 f(x)=0 的根就等於求 p(x,y)=0, q(x,y)=0 的共解。p(x,y)=0 及 q(x,y)=0 在 xy 平面上各代表一條曲線，所以 Gauss 的主要論點就是在說明這兩條曲線一定會有交點的；這個交點所對應的 z 值，自然就是 f(z)=0 的根了。

Gauss 的第二個證明用的是兩個多項式的結式 (resultant)。若 $g(x)=a_m x^m+a_{m-1} x^{m-1}+\cdots+a_0$ 、 $h(x)=b_n x^n+b_{n-1} x^{n-1}+\cdots+b_0$ 為兩個多項式，則行列式

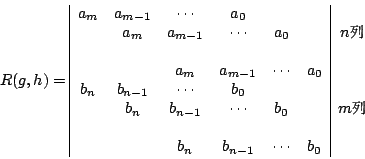
$\begin{displaymath} R(g,h)= \begin{array}{\vert cccccc\vert c} a_m & a_{m-1}&\cd... ...& & & & &\\ & & b_n & b_{n-1}& \cdots & b_0 & \\ \end{array}\end{displaymath}$

就是這兩個多項式的結式。g(x)=0 與 h(x)=0 有共解的條件是 R(g,h)=0，以 g(x)=x(x-a)=x²-ax, h(x)=(x-1)(x-b)=x²-(1+b)x+b 為例，

$\begin{displaymath} R(g,h)= \begin{array}{\vert cccc\vert} 1 & -a & 0 & 0 \\ ... ... &-(b+1)&b& 0 \\ 0 & 1 &-(b+1)& b\\ \end{array}=(a-1)b(a-b) \end{displaymath}$

所以當 a=1 或 b=0 或 a=b 時，R(g,h)=0，而此時 g(x)=0，h(x)=0 有共解顯然是對的。

如果 f(z) 的次數 n 為奇數，則 f(z)=0 至少有一實根，這是因為 z 是很大的正實數時，f(z) 與其首項係數同號，而當 z 是很大的負實數時，f(z) 與其首項係數異號，所以由中間值定理，可知 f(z)=0 必有一根（見圖一），

圖一：f(a)f(b)< 0，所以f(x)=0有解。

當 n 為偶數，且只含 2 的一次因數時，Gauss 考慮

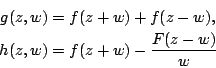
$\begin{eqnarray*} g(z,w)&=& f(z+w)+f(z-w),\\ h(z,w)&=& f(z+w)-\frac{F(z-w)}{w} \end{eqnarray*}$

它們對 z 而言各為 n 次及 n-1 次。它們的結式 R(g,h) 為 w 的 n(n-1) 次多項式，但是因為在 g 與 h 中，w 的奇次項並不出現，所以 R(g,h)=0 可以看成 t=w² 的 $\frac{n(n-1)}{2}$ 次方程式；它是奇次的，所以有個解 t=t₀。因此 $g(z,\sqrt{t_0})=0$ 與 $h(z,\sqrt{t_0})=0$ 有共解，此共解必為 $f(z+\sqrt{t_0})=0$ 的解，由此得知 f(z)=0 有解。如果 n 含有 2 的二次以上的因數，則一再使用結式，也可以得到同樣的結論。

Gauss 的第三個證明，用的是複變函數的積分理論，相當深入，在此略過不表。

Gauss 對代數學基本定理所給的證明是劃時代的。從希臘以來，數學的實體必先找到，才能談它的性質；也就是說證明的過程必須從已知的量出發，一步一步作出中間過程的補助量，以達到最後所要的量。這是所謂建構型的證明。 Gauss 的方法卻不按步就班，他只用學理肯定所要量的存在性，而所要的量是否按步就班可得，卻不是證明所關心的，這是一種存在型的證明。

從 Gauss 開始，存在型的證明逐漸蔚為風氣，變成現代數學的特色之一。

對外搜尋關鍵字：
．代數學基本定理
．Cardano
．Euler
．d'Alembert
．Lagrange
．Wallis
．Gauss
．建構型的證明
．存在型的證明

附錄：另一種證法（高中生也能懂的）

假設 $f(z)=a_n z^n+a_{n-1} z^{n-1}+\cdots+a_0$ ，當 z 點離原點很遠時，也就是當 |z| 很大時，因為

$\begin{eqnarray*} \vert f(z)\vert& \geq & \vert a_n\vert\vert z\vert^n-(\vert a_... ...vert z\vert}+\cdots +\frac{\vert a_0\vert}{\vert z\vert^n})]\\ \end{eqnarray*}$

所以 |f(z)| 可以變得很大。由此可知，這個曲面在較遠的部分，高度會變得很大，所以從幾何圖形的觀點來看，整個曲面會至少含有一個最低點 f(z₀)。我們的目的就是要說 |f(z₀)|=0，亦即 f(z₀)=0。

圖二

如果不然，則 |f(z₀)>0|。畫個圖來說（見圖二），這表示 f(z) 決不會落入以原點為中心，|f(z₀)| 長為半徑的圓內。我們考慮 z₀ 附近的點 z₀+w，觀察 f(z₀+w) 的變化情形：

$\begin{eqnarray*} f(z_0+w)&=& a_n (z_0+w)^n+a_{n-1}(z_0+w)^{n-1}+\cdots+a_0 \\ ... ...inus0.1pt{\fontfamily{cwM2}\fontseries{m}\selectfont \char 225}} \end{eqnarray*}$

令 $w_0 = r_0(\cos{\theta_0}+i \cos{\theta_0})$ , $w = r(\cos \theta+i \sin \theta)$ ，則

$\begin{displaymath} w w_0 = r_0 r[\cos(\theta_0+\theta)+i \sin(\theta_0+\theta)] \end{displaymath}$

我們可以選適當的 θ 角及很小的 r 值，使得 f(z₀)+w₀ w 落入圓圈內，而且當 r 值夠小時，含 w² 因數的各項，對 f(z₀+w) 的位置不會引起有意義的變化，也就是說 f(z₀+w) 會隨著 f(z₀)+w₀ w 也在圓圈內。這就與先前圓圈內無值的假定相矛盾了。也就是說 |f(z₀)|>0 的假定不能成立。


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：洪瑛 ∕ 繪圖：簡立欣

最後修改日期：3/19/2002