���D���ԭz����²��A���ӫ䤧�U�A�o�o�{��ä���²��C�o�D�z�������աA�]���i�U�`����k��b�Ӧh�F�A�n�@�@����O���i��C
���F�n�J�A�W���һ����x���A�ƾǮa�����Ҽ{�X�ؤ���i�ର�H�̱ĥΪ���k�A
�o�Ǥ�k�ҥH���`�ĥΡA���b�O�ѩ�ı�W�{�����̥i�Q�Ħ�C���M�A��ı���{�w�����O���i�a���A�ҥH�̦n��z�פ���C�U���N���ФT�إi���k�A�ä�����u�H�C
- ��k�@�B�C���ҧ��U��` 1 ���C�]��M�A�o�˪��U�`�k�̫O�u�A�ڭ̺٤����O�u���U�`�k�C�^
- ��k�G�B�����ҤU 1 ����`�C�Y�LĹ�F�A�h�U�����U 1 ���F�Y��F�A�h�N��`�[���A�̦������C�������A����u�n�@Ĺ�A�L�N�U 1 ���A�_�h�N��U�`���B�[���C���M�A�ڭ̰��]�ҤU���B�O�X�z���C�]��M���o�ؤU�k���z�ѬO�]���u�n�@Ĺ�A����D���Ҧ��骺���B�Y�����^�ӡA�åB�ϦhĹ 1 ���A�ڭ̩h�B�٤����餣�_���U�`�k�C�^
- ��k�T�B�u�n�\�i�A�ҴN�N�Ҧ��䥻�U�`�A�]���u�n�@���A�Y�ҴN�奻�L�k�C�]��M�o�ؤ�k�O�̤j�x���A�ڭ̴N�٤������ݫ��U�`�k�C�^
�A�|�ĥέ��ؤ�k�O�H��ӹD�z�X�ӶܡH�ƹ�W�A���רä�²��A���� p �s���j��B����Τp�� 1/2 �����A�]�Y��A�O�_����a�j�����C�ڭ̴N�| c=2 ���Ҥl�ӻ����C����K�p�A�ڭ̥H�u�ϡv����Ĺ�A�H�u�Сv���ҿ�A�åH�ϡB�ЩҧΦ������C���ܥҦb���ɧ���Ĺ�����ǡC
�����ڭ̦Ҽ{�O�u���U�`�k�A���ɥu���b�U�C�ѳ��X�A�Ҥ~�|Ĺ�]�Y���a�䥻����^�C
++,
+-++,-+++,
+-+-++,+-+++,-++-++,-+-+++,
    �C �C
�b�Ĥ@�C �ϡ� ���A�ҳsĹ�⦸�A�������v�� 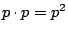 �C�b�ĤG�C���A��Ĺ�F�T���A��F�@���A�åB����إi��ʡA�ҥH����v�� �C�b�ĤG�C���A��Ĺ�F�T���A��F�@���A�åB����إi��ʡA�ҥH����v��
 �]q ���骺���v�A�G p+q=1�^�C�̦����ɥi�o�b�� n �C���A��Ĺ�F n+1 ���A�ӿ�F n-1 ���A�åB�� 2n-1 �إi��ʡA�ҥH����v��
2n-1pn+1qn-1�C�]���i�o�b����ɧ����A��Ĺ�����v�� �]q ���骺���v�A�G p+q=1�^�C�̦����ɥi�o�b�� n �C���A��Ĺ�F n+1 ���A�ӿ�F n-1 ���A�åB�� 2n-1 �إi��ʡA�ҥH����v��
2n-1pn+1qn-1�C�]���i�o�b����ɧ����A��Ĺ�����v��
�{�b���ڭ̦Ҽ{�餣�_���U�`�k�C���ɥu���b�U�C�ѳ��X�A�Ҥ~�|Ĺ�C
++,+-+,
-+++,-++-+,�]�`�N�G�ҲĤG���ȯ�U�` 1 ���^
-+-+++,-+-++-+,
 , ,
 , ,
�C
��W���p��A�i�o���ɥ�Ĺ�����v��
�̫�]�Y�ұķ��ݪk�A�h�ҲĤ@���Y�U�`2���A�]���@���N�M�w�F��Ĺ�A�ҥH��Ĺ�����v�� p �C
�{�b�ڭ̦A�^�����D�G�s���b�o�T�ؤ�k���A�H���ؤ�k�̦n�H�ѩ�۹���Ĺ�����v�����w�D�o�A�ҥH�ڭ̥u�ݱN p �ȥN�J�A�i�Ӥ����j�p�Y�i�A�|�Ҩӻ��A�� 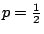 �ɡA�T�̤��ȬҬ� �ɡA�T�̤��ȬҬ� 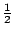 �F�ӷ� �F�ӷ� 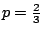 �ɡA�T�̤��Ȩ̧Ǭ� �ɡA�T�̤��Ȩ̧Ǭ� 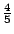 �B �B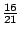 �B �B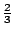 �F�ܩ�� �F�ܩ�� 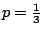 �ɡA�h��Ȩ̧Ǭ� �ɡA�h��Ȩ̧Ǭ� 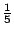 �B �B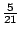 �B �B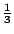 �C
�o�Ǽƭȧi�D�ڭ̡A�� �C
�o�Ǽƭȧi�D�ڭ̡A�� 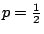 �ɡA�T�ؤU�`�k�S�v�T��Ĺ�����|�F�� �ɡA�T�ؤU�`�k�S�v�T��Ĺ�����|�F�� 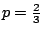 �ɡA�h�H�O�u�k���n�F�� �ɡA�h�H�O�u�k���n�F�� 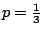 �ɡA�o�H���ݪk�̨ΡA�O�u�k�̮t�C �ɡA�o�H���ݪk�̨ΡA�O�u�k�̮t�C
�o�ǵ��סA�O���O���ǥX�A�N�ƩO�H�����D�٨S�����ѨM�A�����ڭ̶ȴN�O�u�B�餣�_�B���ݤT���ӧ@����C�O�_�|����L�����U�`�k�|�ϱo���ק�n�H�٦��A�ڭ̶ȴN�S�ҨӦҼ{�A�b�@�몺���ΤU�A���פS�O��˩O�H
�{�b�A����̤@��ʪ����G�g�b�U���A�䤤 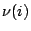 �N�����Ҧ� i ���ɷ|Ĺ�����v�C �N�����Ҧ� i ���ɷ|Ĺ�����v�C
- ���p�@�G
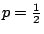
���ɤ��ץҦp��U�`�A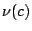 �ڵ��� c/(m+c)�C �ڵ��� c/(m+c)�C
- ���p�G�G
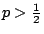
���ɤ��ץҦp��U�`�A
![$\nu(c)\leq[1-(\frac{q}{p})^c]/[1-(\frac{q}{p})^{m+c}]$](img21.gif) �A�ӥk�ݬ��O�u���U�`�kĹ�����v�C�]���A�b�����p�H�O�u�����U�`�k����í���C�t�@�譱�A���ݤU�`�k��Ĺ���̧C�C �A�ӥk�ݬ��O�u���U�`�kĹ�����v�C�]���A�b�����p�H�O�u�����U�`�k����í���C�t�@�譱�A���ݤU�`�k��Ĺ���̧C�C
- ���p�T�G
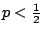
���ɥH���ݪk�̨ΡA�O�u�k�̮t�C�P�˦a�A�O�u���U�`�kĹ�����v��
![$[(\frac{q}{p})^c-1]/[(\frac{q}{p})^{m+c}-1]$](img23.gif) �C �C
�{�b�ڭ̴N�Ӭ�s�A������|���o�ӵ��סI�o�Ψ�F�@�ǼƾǤu��A���L��䤤�������������A�]�U�Υ��媺�iŪ�ʡA���̥u�ܧ�n���ԭz�@�U�C
�ѩ�b�W���������ءA�O�u�k�B��@�ө~�����a��A�ҥH�ڭ̥��N���k�i��Q�סA
�M��A�i�@�B��s��Ӱ��D�C
�p�P�H�e�A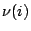 �N�����ҩҾ֦����ꥻ�F i ���ɡA�L�|Ĺ�����v�C�ѩ�Ҥβ��a���`�ꥻ�B�� m+c ���A�ҥH i ���i��Ȭ� i = 0, 1, �K, m + c�C��M�a�A �N�����ҩҾ֦����ꥻ�F i ���ɡA�L�|Ĺ�����v�C�ѩ�Ҥβ��a���`�ꥻ�B�� m+c ���A�ҥH i ���i��Ȭ� i = 0, 1, �K, m + c�C��M�a�A �A �A �A�� �A�� 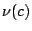 ���ڭ̳̦��ҷQ�D�o�����v�C ���ڭ̳̦��ҷQ�D�o�����v�C
- ���p�@�G
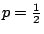
���w�Y�Ҳ{�� i ���A���� 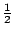 �����|�A�L���ꥻ�|���� i+1 �� i-1 ���C�]�� �����|�A�L���ꥻ�|���� i+1 �� i-1 ���C�]��
�o�˪���� �h�A�b�ƾǤW�O�@�ӽu�ʨ�ơA�]���Ѫ��q���� 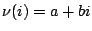 �C�ѩ�A �C�ѩ�A �B �B �A�o a=0�B �A�o a=0�B
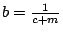 �C�]�� �C�]��
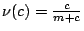 �A��Y�Ҫ�Ĺ���� c/(m+c)�C �A��Y�Ҫ�Ĺ���� c/(m+c)�C
- ���p�G�G
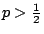
�O q=1-p�C���ɹ� �h �ڭ̦���{��
�o�˪��@�դ�{���A�b�ƾǤW�٧@�O�t����{���C���]���@�ӨD�Ѫ��@���k�A����D�z���`�C�������G�A�ڭ̯S�ĥΤU������k�C
�Q��p+q=1�A�W�դ�{���i��g��
����ۥ[�A�çQ�� 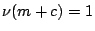 �B �B �A�o �A�o
�Y���e c ���ۥ[�A�h�o
- ���p�T�G
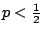
��G���Ѫk�A�i�D�o
�O�u�k�� 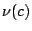 �w�D�o�A�{�b�ڭ̨Ӭ�s������b���p�G�ɡA�H�O�u�U�`�k�� �w�D�o�A�{�b�ڭ̨Ӭ�s������b���p�G�ɡA�H�O�u�U�`�k�� 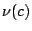 ���̤j�F
�Ӧb���p�T�ɡA�ϥH�O�u�U�`�k�� ���̤j�F
�Ӧb���p�T�ɡA�ϥH�O�u�U�`�k�� 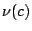 ���̤p�F�P�ɥt�@�譱�A�b���p�G�ɡA�h�L�צ�ؤU�`�k�A ���̤p�F�P�ɥt�@�譱�A�b���p�G�ɡA�h�L�צ�ؤU�`�k�A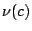 �Ҥ@�ˡC �Ҥ@�ˡC
�����ڭ̤i�@�өw�z�C�O Sn �N���b�� n ���ɧ��ɡA�ҩҾ֦����ꥻ�B�A�]�� Sn �O�@���H���ܼơC�ڭ̨ó] S0=c�A�Y��ꥻ�C�O N �������ɧ��һݤ��ɶ��A�]�� SN=0 �� c+m�C�ڭ̨åH E ������ȡC
- �w�z�G
- �] f ���@�w�q�� Sn �W�����ɨ�ơC�Y�b Sn ������U�Af(Sn+1) �������
E[f(Sn+1)] = f(Sn)�A�h
E[f(SN)] = f(S0) = f(c)�C
�Y�N�u=�v�אּ�u
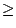 �v�A�h���ץ�u�C �v�A�h���ץ�u�C
���w�z�b���v�ǤW�A�Y�ۦW����ܼ˥��w�z (optional sampling theorem)�A�����ҩ��w�W�L���Z�{�סA�ҥH���h���ҡA���������[�N�q�o�����F�ѡC�N���u=�v�����Ψӻ��A���O���Y�A���� n+1 ���ɧ��A�����Ө��ä�����ܦb�� n ���ɧ��� f ���ȡA�h������ɧ������ɡAf �������Ȥ]�P����Ȥ@�ˡC�t�@�譱�A�Y�b�u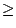 �v�����p�A��Y�A���� n+1 ���ɧ������Ө��|��i f ���e���ȡA�h���ɧ������ɡAf �������Ȥ]�������Ȭ��ΡC �v�����p�A��Y�A���� n+1 ���ɧ������Ө��|��i f ���e���ȡA�h���ɧ������ɡAf �������Ȥ]�������Ȭ��ΡC
�{�b�ڭ̴N���o�w�z���ҩ����e�ڭ̩ҤU�����סC
�����A�ڭ̦Ҽ{���p�@�C���ɨ� f(Sn)=Sn�A�h�����ؤU�`�k�A�]�ӭt���|�����A
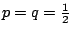 �A
�ҥH�Y���w Sn�A�h
ESn+1 = Sn�C�]���ѤW�w�z�� ESN = c�C�� �A
�ҥH�Y���w Sn�A�h
ESn+1 = Sn�C�]���ѤW�w�z�� ESN = c�C��
![$ES_N = (c+m)\nu(c)+0[1-\nu(c)]$](img38.gif) = = 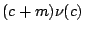 �A
�ҥH�����ץH��ؤ�k�A �A
�ҥH�����ץH��ؤ�k�A
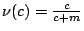 �C �C
�ܩ�b���p�G�ΤT�ɡA�ڭ̨�
 �C���ɭY���w Sn�A�h �C���ɭY���w Sn�A�h
�䤤 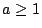 ���ҤU�`�����B�C�Q�� ���ҤU�`�����B�C�Q��
�i�o���ץH��ؤU�`�k�U�`�A�Y���w Sn�A�h
![$E[f(S_{n+1})]\geq f(S_n)$](img45.gif) �C�ҥH�ѩw�z�� �C�ҥH�ѩw�z��
![$E[f(S_N)]\geq(\frac{q}{p})^c$](img46.gif) �C
�� �C
��
�]���i�o�b���p�G�A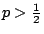 �ɡA �ɡA
�Ӧb���p�T�A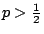 �ɡA �ɡA
��
![$[1-(\frac{q}{p})^c]/[1-(\frac{q}{p})^{m+c}]$](img50.gif) ���ĥΫO�u�U�`�k��Ĺ�����v�A�ҥH���b���p�G�ɡA�H�O�u�k�� ���ĥΫO�u�U�`�k��Ĺ�����v�A�ҥH���b���p�G�ɡA�H�O�u�k�� 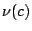 ���̤j�F���b���p�T�ɡA�o�H�O�u�k�� ���̤j�F���b���p�T�ɡA�o�H�O�u�k�� 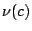 ���̤p�C ���̤p�C
�ܩ���b���p�G�ɡA�H���ݪk��Ĺ�����̧C�F���b���p�T�ɡA�o�H���ݪk��Ĺ�����̤j�C�o�䤤�S�o�A���`���z�סA�u�n�q���F�C
|