曹亮吉

實數除了常見的整數、分數，還有無理數。除了數學家，一般人對實數（尤其是無理數）的了解實在有限得很。即便是數學家也要到十九世紀後半，才完全弄清楚實數到底是什麼，那麼，在此之前，人類怎樣摸索實數的意義呢？

在中國，很早就能應用分數與小數，遇有根號。就用開方法，求得近似值。中國的數學以應用為主，關心的是怎樣求得近似值，從來也不問 2 的平方根到底是什麼，更不用說會問：除了有根號的數外還有什麼樣的數？

巴比倫人也講求實用，他們心目中的數就是六十進位的整數及有限小數。古埃及人就有點不一樣，也們不懂得小數，而分數都要化成分子為 1（分母各不同）的小數之和才能計算（如 ）。可想而知，這種算法非常笨拙，無疑地妨礙了埃及數學的進展。當然，這種埃及分數是很有趣的數學題材，但不是本文討論的要點 ^註1。

古希臘的數學掌握在哲學家手中，注重的是理論，根本瞧不起實際的計算。他們對數的看法持原子論，認為宇宙的一切事物都可以用自然數或兩自然數之比來了解。可是他們並不把比當做數來看待（只有商業計算才用分數，但那不是數學家的事），因此所謂「數」就是自然數。

「等腰直角三角形斜邊與一股之比（）不是自然數之比」，這件事的出現使原子論陷於困境。Eudoxus (408-355B.C) 於是創比例論，用幾何方法處理同類兩幾何量之比，暫時使希臘的數學基礎脫離此困境^註2。 由於比例論的成就，使得幾何學成為希臘數學的主流，代數問題幾乎全用幾何方法來處理。另一方面，比例論雖然解決了一些無理比的問題，但它都還是不把量比當做數，使得算術和代數的發展受到阻礙，這是古希臘數學的最大缺陷之一。

由於代數的問題用幾何方法處理，也由於古希臘的幾何學限於直尺與圓規，所以古希臘所能處理的數，就是尺規所能做出的「數」，也就是尺規所能做出的長度（與單位長度相比的比值），透過這種幾何方式，希臘人試圖了解由整數經四則運算及開方運算所得的「可做數」^註3。

古希臘的幾何三大難題，倍立方、圓化方及三分角，其實就是想要造出 、π 及某類三次方程的根這些數。希臘人萬沒想到他們的幾何方法有時而盡，居然這些數是用尺規造不成的。希臘人看不出尺規作圖和四則運算或開方之間會有什麼關係，這種代數問題只有等到代數成熟之後的十九世紀才得解決^註4。

亞歷山大時期的希臘數學學風漸有改變。天文、三角採用小數計算，實用問題不再完全摒棄，小數、分數才納入數的系統。我們把分數又叫做有理數 (rational number)，其實 rational 源出 ratio，應該譯成比數才對，才合乎原來的意思。至於 irrational 當然是非比數，譯成無理數真是無理之至。但約定俗成，我們還是接受通用的譯名。此期，阿基米德、Heron、Ptolemy 等人，用了很多分數做為平方根的近似值，另一方面，帶根號的「量」偶而也看做純粹的數來處理，但絕不像幾何那樣有嚴格的邏輯基礎。印度人和阿拉伯人更進一步，他們不但把帶根號的量當做數，而且這些數之間也可以做代數式的運算。他們不像希臘人那樣哲學心重，計算的需要使他們只重算，而未觸及無理數的邏輯問題。

西元1500年以後的歐洲，無理數的使用更加自由。譬如 Stifel（1486∼1567年）研究 型的無理數；Vieta（1540∼1603年）考慮圓內接正 2ⁿ 邊形，而得^註5

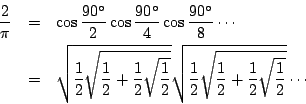
雖然有些歐洲數學家把無理數當做數，但受到希臘幾何學的影響，許多數學家如 Pascal（1623∼1662年）、Barrow（1630∼1677年）、Newton（1642∼1727年）等都認為： 若脫離幾何就沒有意義，所以只有 這種量比，沒有 這種數。這種對無理數之不安，可用 Stifel 的話做代表^註6：

「在證明幾何圖形時，有時候有理數不管用，而無理數取而代之，居然很管用。這使我們不得不承認無理數確實是數。可是其他的理由卻使我們不得不放棄這種想法。亦即，當我們用小數表示無理數，我們發現小數沒有個結尾。既然它是那麼不確定，它就不是真正的數。因此，就像無窮大不是一個數，無理數也不是真正的數，它躲藏在一種無窮的雲霧裡。」 ^註7

雖然如此，由於三角的需要、對數的發展等，使得數學家漸漸接納無理數為數，且使用無窮小數、無窮連分數。無窮數列。無窮乘積、無窮級數等方法來逼近無理數。十七、十八世紀，由於微積分的出現，使大家亟亟於應用這個犀利的新工具，而少做理論性的討論，只有十八世紀少數幾個數學家在無理數的理論探討方面有些小突破。

1737年，Euler 將自然對數的底數 e 用連分數展開，發現它是個無窮連分數，因此證得 e 是無理數（他同時也證明 e² 是無理數） ^註8 。J.H. Lambert（1728∼1777年）也用連分數的方法證明下面的重要結果：若 x 是不為 0 的有理數，則 e^x、 都是無理數。根據這個結果，既然 不是無理數，那麼 ，因此 π，不能是有理數。

Legendre（1752∼1833年）更猜測說：π 不但不是有理數，不是帶根號的無理數，而且也不是任何整係數多項式方程式的根。滿足一個整係數多項式方程式的數稱為代數數，否則稱為超越數──超越了代數的方法。代數數（如整數、有理數、可做數都是）和超越數的區分，是十八世紀研究無理數在觀念上的小突破，可是終此世紀，數學家沒法找出一個超越數來。

大致說來，在十九世紀以前，無理數是位無法理解的數。