漫談費布那齊數列 (第 3 頁)

　1│2│3│4　

漫談費布那齊數列（第 3 頁）

黃敏晃;方述誠

首頁 | 搜尋

．原載於科學月刊第五卷第七期
．作者當時任教於台大數學系

‧註釋
‧對外搜尋關鍵字

費氏數列的一些性質

費氏數列，也可以由楊輝三角中得到。楊輝三角又叫巴斯卡三角 (Pascal trinangle)。楊輝三角是由 (n+1)ⁿ 的展開式中，各項係數所構成的。在下表中，我們可以看到其間的關係：

由上表，不難聯想到費氏數列中各項，與組合數 Cⁿ_k 之間的關係是 ^註1

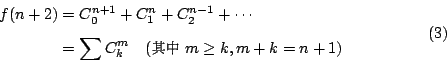
$\begin{displaymath} \begin{eqalign} f(n+2) &= C^{n+1}_0+C^n_1+C^{n-1}_2 + \cdots... ...ectfont \char 50} } m\geq k, m+k=n+1) \end{eqalign} \eqno{(3)} \end{displaymath}$

費氏數列除上述的(2)與(3)的性質外，還有下列的關係；其中甲、乙、丙、丁諸陳述是比較簡單的，戊、己則比較困難，所以附上例子。至於這些關係的證明，就此省略，請讀者自行研究：

甲、 $f(1) + f(2) + \cdots + f(n) = f(n+2)-1$ 。

乙、 $f(1) + f(2) + \cdots + f(10) =11 f(7)$ 。

丙、 f(n)f(n-1)-f(n-1)f(n-2) = f(2n-1)。

丁、 f²(n-1) + f²(n) = f(2n-1)。

戊、如果f(p)是個質數(p>4)，則p必然是個質數。例如，f(11)=89 為質數，則 p=11 也是質數。注意，此性質的逆陳述並不成立。例如，31是個質數，但f(31)=1346269=557×2417。

己、 (1)如果 p 是 $10k\pm 1$ 形式的質數，則 f(p) 成 pa+1 的形式，其中 a 與 k 為整數。

(2)如果 p 是 $10k\pm 3$ 形式的質數，則 f(p) 成 pb-1 的形式，其中 b 與 k 為整數。

例(1)

$\begin{displaymath} \begin{array}{c\vert c} p=10k\pm 1&f(p) \\ \hline 11&89=11\t... ...mes 43428+1 \\ 41&165580141=41\times 4038540+1 \\ \end{array}\end{displaymath}$

例(2)

$\begin{displaymath} \begin{array}{c\vert c} p=10k\pm 3&f(p) \\ \hline 7&13=7\tim... ...\times 1246-1 \\ 37&24157818=37\times 652914-1 \\ \end{array}\end{displaymath}$

　1│2│3│4　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：陳文是 ∕ 繪圖：簡立欣

最後修改日期：6/17/2002