�K���J���D �]�� 2 ���^
���ӱX
�D������Ǥ�Z�ĤT���Ĥ���
�D�@�̷��ɥ��Щ��ƾǨt
�E����
�E��~�j�M����r
|
�K���J���D �]�� 2 ���^ ���ӱX
|
�D������Ǥ�Z�ĤT���Ĥ��� �D�@�̷��ɥ��Щ��ƾǨt �E���� �E��~�j�M����r |
���F²�Ƴ\�h�����n���W���A�H�W�����D�i�H�Q���@�ӳU�l�̦�N�Ӳy�C�C�Ӳy�W�����b�|���ƥءC���w�b�|�����ۦP�A �j�p�ڭ̤����D�C�ڭ̨C���H�K���@�Ӳy�X�ӡA�ݤF�b�|����N�o�M�w�n���n�C�p�G�n�A���y�N������C�p�G���n�A �A���U���A������A�^�Y�n������y�C�o�ˤU�h�A����N�Ӳy��������C�ڭ̪��ت��O���쨺�ӳ̤j�b�|���y�C 1
�b���ڭ̩w�y�����Ŭ�;�̤j�y��N���A���j�y��N-1���A
���ڭ̨��X�Ĥ@�y�ɡA�ڭ̬ݨ������b�|�Or1�A�������������šC�{�b���G�ӿ�ܡC�@�O�ڭ̴N�n�F���A
�G�O�ڭ̤��n���A���U�@�ӬݬݡC�p�G�ڭ̭n�F���A�ڭ̮���̤j�y�����|��M�O
�p�G�ڭ̤��n���A�ڭ̬ݨ�F�ĤG�Ӳy���b�|�Or2�C�ڭ̤S���G�ӿ�ܡA�n���n��?�p�G�ڭ̴N�n�o�ĤG�Ӳy�A
�ڭ̮���̤j�y�����|���O
�P�z�A���ڭ̬ݨ�ĤT�y���b�|r3�ɡA�ڭ̪���ܬO:
�p���A�ڭ̪��@��W�h�O�G
�{�b�ڭ̥H�|�y���ҡA�ݬݱ��Φp��C�ڭ̥H 1,2,3,4 ���ܲy�����šA�]���@�^���ܥ��̪��X���ǡC
�ھڱƦC����k�A�@��
���ӤW�z���W�h�A�Ys=1�A�N�O�ڭ̴N�n�Ĥ@�ӡA�ڭ̦�6�رƦC�k�i�H����̤j��(�Y�ĥ|�C������)�A
�]���ڭ̮���̤j�y���εM�v�O
�Ѧ��i������̤j�y�̦n����k�O�Os=2�A�]�N�O���V�L�Ĥ@�y�A�q�ĤG�y�}�l��j��Ĥ@�y�����Ӳy�C
��@��N�Ө��A�ڭ̭Y�q��s�y�}�l����A�ڭ̮���̤j�y���εM�v�O
2
�G
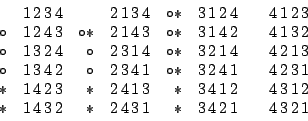
���@:�|�y���X����
���G�G�̨βq�y�k,�u�q�@��.N���ܲy��,s*���ܶ}�l�i�n���y,PN(s*)���ܲq�諸�εM�v.
�q�W�����A�ڭ̤����N�J�Ҧ���
�q���G����ܥX�A���y�ƷU�h�ɡA�Y�ϧڭ̥γ̦n����k�A���̤j�y�����|���|��p�C�o�ä����Q���A
�]���y�h�F�A���ߤ@�̤j���N����F�C�ھڲz�פW������
3
�A�o�εM�v�ä��ͪ��s�A
���ͪ��e-1�C�o�q��e�O�۵M��ƪ����A������2.72�C�]���ڭ̬ݨ�A���زq�k�q�諸�εM�v�û��j��
|
�b�K���J���D���A�p�G�ڭ̧�����e�@�I�A���\�p�k�ĥ��K�@�K�A�M��i�H�A���@���A��ܪ���k�S�p��O? �ڭ̤����Q���o���M���䰨����k�b��`�ͬ����O�ܱ`�����C���L�������Ƥ���Ӧh�A�_�h�@����j�����U�h�A �@�w�i�H����̤j�����ӡC�ڭ̰��w�u�ഫ�@���C
���M�^�쮳�y�����D�W�ӡC�{�b�ڭ̤��\�q�y�̴��@���C�����ڭ̤]�\�|�Q������Ĥ@�ӡA�M�ᵥ�@�q�ɶ��A�A�ݤj�����C
�ھڰ��D���@�P�˪����z�A�ڭ̥i�H�ݥX�����Ĥ@�Ӫ���k�ä����o�̦n�A�]���Ĥ@�ȬO�̤j�y���εM�v�u��
�bR(t,s)���A�Ys=t+1�A�h���ܨ��L�Ĥ@�y����A�ߨ�N�i�H���C�o�Ӱ��D�b�p��W����D���@�����ܦh�A �ڭ̤��⤽���C�X�ӡC���T����ܥX�̦n��t�As�ϧڭ̮e�����쨺�ӳ̤j���y�C
���T�G�i���@�y���̨Ψ��k�CN���ܲy�ơAt*�Bs*�Y�Ĥ@���P�ĤG���W�L���y�ơAP���q�諸�εM�v�C
�q���T�ڭ̥i�H�ݥX�A�ڭ̮���̤j�y���εM�v�l�פj��
�J�Ӭݪ��T����s*�A�ڭ̷|�o�{���P���G����s*�ۦP�C�ڭ̬ݥX�{�b����k�u�O���Ϧb�}�l�ɶV�L���y�Ӧh�C
|
�b�e���G�Ӱ��D���A�ؼг��b�̤j�����J�W�C�p�G�̤j�����J�b�e���ڭ̶V�L���a��A�ڭ̴N�����n�F�C �o�ءu�笰�ɸH�v����k�A���ɨä��i���C�b�� (�@)�B(�G)�B(�T)���A���q�`�o��@�ӤH�A�ڭ��`�n���Фl�A �Ĥl�`�n�Yī�G�A�̦n�����B���O�H�H�����A�ڭ̦p��h�ӨD�䦸�ɥi���X�̦n���H��A�Фl�A�Pī�G�O?
�A�γU�l�̮��y���Ҥl�ӻ��A���w�ڭ̮���̤p���y�i�o1���A���p���y�i�o2���A�K�A�̤j���y�oN���A �ڭ̥u���@���A����^�Y��A��������@�ӡA�ڭ̦p���~�i�H�o�찪���O?
��M���D�p�G�ڭ��H�K���@�Ӳy�A�δN���Ĥ@�Ӳy�A�ڭ̱o��������ȬO
�p�G���@�ʭӲy�A�H�K�����ܡA�o��������ȬO50.5�A���p�G�ھڲz�ױ��X�̦n�����k�A�ڭ̥i�H�ϱo��������Ȱ��F97.4�C �ѨM�o�Ӱ��D�������P�t��۷��������A���ڭ̨ä������X�ѨM�����D����V�C
�ڭ̬J�n�V�L�Ĥ@�y�A�P�z�ڭ̤]�i�H�V�L�e���Y�z�Ӳy�C���w�y��N=10�A���w�ڭ̶V�L�e�T�y�C�p�G�ĥ|�y�����Ƥ�e�T�y�����A �ڭ̦۵M����(�_�h�ڭ̴N�w���V�L�e�|�y�F)�C�p�G�����ƧC�A�ڭ̮��Ĥ��y�A�����A�p�G�ڭ̮���ĤK�y�A�٥��J����ư����y�A �ڭ̴N�o�p�ߤF�A�]���ҳѪ����|�w�g���h�A�ĤK�y�����ƧY�Ϥ��ܰ��A�p�G�u���ˡv���ܡA �ڭ̴N�i�H�n�F�C�Ҧp�ĤK�y�O�w���y�����Ʀ�ĤG�쪺�A�ڭ̴N�Ө��U�F�C�p�G�ĤK�y��b�ܤp�A �ڭ̤����A�ղĤE�y�A�������o���C�F�C�p�G�ĤE�y�b�e���E�Ӳy�����Ĥ���H�W�N�ȱo�n�F�A �]���̫�@�y�������(���ɧA�D�n���i)�u��5.5�C
�]���A���D�����k�O
��@��N�Ө��A����L���c���A�ڭ̥u�|N=4���ҡA�ݳ̨Ϊ����k�p��CN=4�ɳ̨Ψ��k�O:
�p�����k���o������Ȭ� 3.125�A���H�K����2.5�j�F���֡C��@��j N �Ө��A�̪�V�L���y�Ƭ�����
|
�K���J���D�٥i�H�Ψ��k�k�B�ͤW�h�C��ڤW�D�o�Ӱ��D�b�\�h�ƾǩβέp���x�W�N�O�H�u������D�v�Ρu�B�ð��D�v�o�����C �ڭ̭ɥε����ت��հ����l�P�˪L���D�ӰQ�צ����D���t�@�o�i�C
�˪L���D���b�űC�a�q�A�űC���T�Ӥk��C���@�Ѥ��l��űC�a���e�ӱa���D���C�L���{�o�֬O���D�֬O�űC���k��F ���L���D���D�O�̺}�G���C(�űC�k��]������A�_�h�N�Ӯe���q�F�C)�q���覡�P���D�@�ˡA�k�Ĥl�@�ӭӥX�ӡA �e���X�ӫ���i�h�A���l�o�ߨ�U�M�߱a���a�o���A����^�Y�a�C���l���ت��O�{�X���D�C��ثe����P���D���@�����@�ˡC �{�b�t�[������O�A�űC���v�w�Ƥ��D�X�������ǡA�o���Ʊ���l�{�X���D�C
���w���l�����h�ѡA�ӧűC�o�]���p�h�ݡA�G�ӳ��O�����o�����H�C�{�b�ݡG�Ӱ��D���@���Ѫk�A ���l�̦n����ܪk�N�O�V�L�Ĥ@��X�����k�Ĥl�A�q�ĤG��}�l����A�a��Ĥ@��}�G���^�a�C ���űC�o�]���D���D���@����k�A�o�⤽�D��b�Ĥ@��A���l���N���ѤF��?�����l�����O���z�D�L�]�|�Q��o�I�A �q�Ĥ@�줣�N�Ǧ��\�F��?���űC��D�L�ध���A�o�⤽�D����ĤG��N�O�F�K�C�p���Ĥ߰����A��F�{�H���ɨ�A ���l����˻{�A�űC����˱ơA�~�i�H�y���ۤv�̦��Q���Բ��O?
�����ܩ��㪺�@�I�O����n���Բ������O�T�w���ӬO�εM���C�������A�Y�űC�̦n����k�O�⤽�D��b�ĴX��X���A ���l��i�P�˱��X�o�Ӧ�m�A���G�@�q�Y���A�i���űC�L�T�w�ƪk�C�t�譱�A�p�G���l�̦n����k�O 1.�a���Ĥ@��A�α��@��L����� 2.���a�Ĥ@��A�űC���i�H�ϥL���ѡC�]���L���q�k�]���O�T�w���C �εM���Բ��O�o�˪�:�űC�H�εM�v p1 �⤽�D�Ʀb�Ĥ@��Ap2,p3,p4�A�⤽�D��b�ĤG�B�T�B�|����m�C ��ɭ��{�ɩ��ҩΥ��l(�H�W�z���εM�v)�w�Ƥ��D����m�C���l�i�H��X�űC�����t�k p1, p2, p3, p4�A ���o�L�k�T�w�ҩλ�l���M�w�C�p�G�ڭ̥� si ���ܤ��l�V�L�e�� i �Ӥk�Ĥl���q�k�A�h���l�n���Բ��]�O�H p1, p2, p3, p4(���@�w�P�űC���ۦP)���εM�v�Ĩ�sO, s1, s2 �P s3 ����k�C
�ڭ̥Hx���ܤ��l���Բ��Ay���ܧűC���Բ��Ap(x,y)���ܦb����Բ��U�A���l�q�X���D���εM�v�C ���l�Ʊ�p(x,y)�U�j�U�n�A�ӧűC�Ʊ�p(x,y)�U�p�U�n�C�]���l�P�űC�����o���A ���w�L�̳����F�L�̪��̨ξԲ�x*�Py*�C����x*�Py*�Ӧ��U�����ʽ�4 �G
�p�G��ӳ����γ̨ξԲ���?�����Ӳ³J�b�@�_�A����ǨƳ��i��o�͡A�ڭ̤������L�̶˸����C
�p��D�X����1���P2����x*�Py*�O�C���� (Game Theory) �������U�A�����n�ιq�l�p����w��C�����D���������רä������C
���w�űC�i�H�H�N�w�Ƴo�|�Ӥk�Ī���m�C�űC�̨Ϊ���k�O�P�H1/4���εM�v�w�ƤU������@�إX���ǡG
����1,2,3,4���O���ܤk�Ĥl�}�G���{�סA4�N�����D�C���l�̨Ϊ��q�k�O�H�K�q�D�L���\���εM�v�O0.25 5 �C
���w�űC�u�i�H�w�Ƥ��D�����ǡA�T�Ӥk�ण�������������᪺�ñơA����űC�̨ξԲ�y*�O�G �H6/17,3/17,2/17,6/17���εM�v�⤽�D�Ʀb�Ĥ@�B�G�B�T�B�|��m�W�C
�Ӥ��l���̨ξԲ�x*�O�G�H 6/17,6/17,3/17,2/17 ���εM�v�� s0, s1, s2 �P s3 ���q�k�C (si �b�e���w�q�L�A�Y���V�L i �Ӥk�Ī���k�C)
�b�o�ر��ΤU�A���l�q�諸�εM�v�O 0.353�A�� 0.25(���l���Τ߭p�H�K�q)�j�A���� 0.458(�űC���Τ߭p�H�K��)�p�C ����έp�A�Ҧ�����A�űC�H���j���εM�v�⤽�D��b�Y���A�ܦX�G�ڭ̪���ı�C
��@�� N �Ө��A�p�G�Y�H�i�H�w�ƥ������X���ǡA�L�i�H�ϲq�̲q�諸�εM�v��� 1/N�C
���p�G�L�u���v�w�Ƴ̦n��(�γ̦n���u���v�M�w�ۤv���ê���m)�A��������賣�γ̨ξԲ��ɡA
�q�̲q�諸�εM�v����
|
|
|
|
|
�]�Y�������B�ðݡK�K�A�i�H�b�� �d�� �� �g�H ���ڭ̡C�^ |
|
|
|
EpisteMath (c) 2000 ������s�|�ƾǩҡB�x�j�ƾǨt �U�����峹���e���ۧ@�v����ۧ@�H�Ҧ� |
| �s��G�H�f�� | �̫�ק����G4/29/2002 |