我們這次討論的主要目的就是Stokes'定理與Gauss定理如何應用到電磁學上面, 然後得到電磁學的方程式, 就是Maxwell's equations, 所以我們來看一下電磁學在實驗上面、在觀察上面有那些基本的現象, 這些現象其實一共只有三個, 我們來看這三個實驗定律:

第一個實驗定律, 我們叫做Coulomb定律

圖3

Coulomb定律也就是說如果有兩個電荷q₁和q₂(如圖3), 這兩個電荷中間有吸引力或排斥力, 相同的電荷相斥, 不同的電荷就相吸, 然後這個力量的大小和q₁q₂成比例, 且和反平方1/r²成比例, 而r就是q₁ 和q₂的距離, 方向是在兩點的連線上, 如果把方向表示出來的話, 就變成 , q₁、q₂可正可負表示相斥或相吸。Coulomb 定律是在1785年左右, 由Cavendish 和 Coulomb 分別做實驗發現的現象, 所有的電磁現象的研究, 也就從這個年代開始。

第二個電磁現象, 我們叫做Biot-Savart 定律, 差不多是在1820年左右由Biot、Savart 及Ampere幾個人所發現的, 它的現象就是說, 假設有兩個線圈, 上面有電流通過, 一個是I₁, 一個是I₂(如圖4)

圖4

我們發現這兩個線圈中間也會有吸引力或相斥力, 這個現象我們叫做Biot-Savart定律。我們曉得電流是由電荷流動產生的, 這個力和庫侖力一樣也是由電荷產生的, 只不過它是由電荷的流動產生的, 雖然是由電荷產生, 但並不是電力, 而是一個新的力, 原因是如果我們把一個磁針放在線圈附近的話, 磁針會受到電流的影響, 產生偏移, 換句話說, 這個磁針會受到電流的作用力, 經由Biot、Savart和Ampere 等等長時間的研究後, 認為電流產生的力和磁針產生的力是同一性質的力, 並不是歸在剛剛我們所講的庫侖力, 這是一個新的力, 我們叫做磁力, 這個力的公式是這樣的:

第三個定律叫做Faraday定律, 是在1831年由Faraday和Henry發現的。 假設我們有一個線圈, 然後我們讓磁場(稍後定義)在這個線圈附近變動(如圖5)

圖5

比如把一個磁鐵放在這個線圈裡面移動的話, 我們便會發現線圈中有電流通過, 所以, 磁場的變動就會產生電流,當然經過實驗之後, 它也可以歸納出一個定律出來, 這個定律可以寫成這個公式:

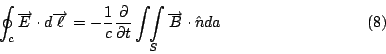
這三個現象都是從自然界所發現的定律, 所有的電磁現象, 都是建立在這三個觀察現象上面(除了一點點重要的小修正外)。