| |
有「內積」就應該有「外積」,聽起來似乎理所當然,
其實並不盡然,只有三維空間中,才有外積的定義。
再說「內」、「外」之分,
似乎是歷史的錯誤;兩個向量的內積,並不是個向量,而是個純量(數),
然而兩個三維向量的外積,卻仍是個向量,絲毫不見「外」。
在三維空間中,兩個向量的外積,可以自然地描述,也可以藉由座標來定義。
設 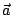 , ,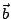 為空間中兩個不平行的非零向量,
其外積 為空間中兩個不平行的非零向量,
其外積
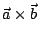 為一長度等於 為一長度等於
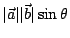 ,(θ為 ,(θ為 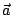 , ,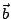 兩者交角,且 兩者交角,且 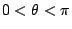 ),
而與 ),
而與 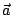 , ,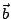 皆垂直的向量。通常我們採取「右手定則」,
也就是右手四指由 皆垂直的向量。通常我們採取「右手定則」,
也就是右手四指由 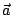 的方向轉為 的方向轉為 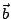 的方向時,大拇指所指的方向規定為 的方向時,大拇指所指的方向規定為
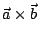 的方向。例如在右手系的空間座標中,
若 的方向。例如在右手系的空間座標中,
若
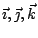 分別代表 x軸、y軸、z 軸正向的單位向量,則 分別代表 x軸、y軸、z 軸正向的單位向量,則
另外,顯而易見的是,
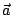 , ,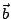 的外積與其次序有關, 的外積與其次序有關,
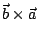 並不等於 並不等於
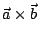 ;
事實上, ;
事實上,
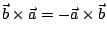 。當 。當 , , 中有一個零,
或者兩者平行時,則令 中有一個零,
或者兩者平行時,則令
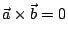 。 。
如果選定一組座標系,
 為對應的三正交單位向量,則 為對應的三正交單位向量,則  與 與  的外積,可藉由其分量表示出來:
若 的外積,可藉由其分量表示出來:
若
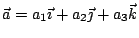 , ,
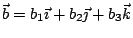 ,則 ,則
假使我們借用行列式的符號,不妨把它寫成
不但容易記,而且也可以經由行列式的性質,驗證一些外積的性質。
這兩個方法,各有千秋,前者易懂,後者好算。借助於座標化,
我們可以透過機械的運算(可能繁但不會難),驗證一些類似
的複雜式子。即使只知道定義,你一樣可以驗證,然而自然的描述法,就很難辦到。
不過,引進座標系來定義,終不免有個疑慮,那就是:選擇不同的座標系,會不會導致不一樣的外積?
由行列式的性質可知,若將
 分別代以a1, a2, a3 或 b1, b2, b3,則(*)之行列式等於 0,也就是說 分別代以a1, a2, a3 或 b1, b2, b3,則(*)之行列式等於 0,也就是說
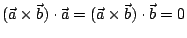 。換句話說, 。換句話說,
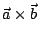 與 與 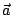 , ,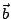 兩向量都正交。
另外 兩向量都正交。
另外
而我們知道,
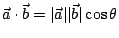 ,因此, ,因此,
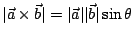 ,總而言之, ,總而言之,
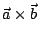 為一長為
為一長為
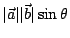 ,而與 ,而與 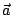 , ,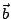 皆正交的向量,可見與座標系的選取無關。 皆正交的向量,可見與座標系的選取無關。
外積的運算,與一般的乘積,有同有不同。相同的是,分配律成立:
不同的是,交換律與結合律並不成立。
(試舉一例,說明
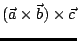 不必等於 不必等於
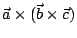 !)
取而代之的是,反交換律 !)
取而代之的是,反交換律
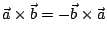 及
Jacobi 恆等式 及
Jacobi 恆等式
另外,純量與向量的混合結合律則無問題:
現在,我們來看一些簡單的應用:
- [例1] 正弦定律
如下圖
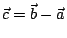 ,故 ,故
 即
即
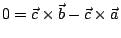 ,故 ,故
 ,
從而 ,
從而
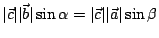 ,因此 ,因此
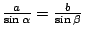 。 。
- [例2] 平行六面體的體積
如下圖,
 垂直於底面,即 垂直於底面,即 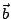 與 與 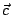 所生成的平面,其長 所生成的平面,其長
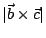
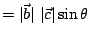 ,也就是底面平行四邊形的面積,因此 ,也就是底面平行四邊形的面積,因此
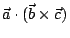
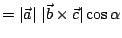 ,
而 ,
而
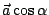 即為高 h,故 即為高 h,故
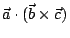 代表 代表 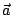 , ,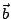 , ,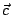 三向量所張之平行六面體的體積。 三向量所張之平行六面體的體積。
若
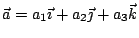 , ,
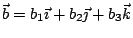 , ,
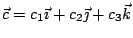 ,則 ,則
又,由行列式的性質,易知
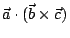
 。 。
- [例3]平行四邊形與三角形之面積
在例2中,若取 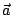 為垂直於底面之單位向量,則平行六面體之體積,即底面平行四邊形之面積。因此, 為垂直於底面之單位向量,則平行六面體之體積,即底面平行四邊形之面積。因此,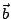 , ,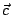 二向量所張之三角形面積,即為此三重積 二向量所張之三角形面積,即為此三重積
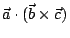 之半。 之半。
例如,平面上三點 P1(x1,y1),P2(x2,y2),P3(x3,y3) 所形成之三角形面積可計算如下:取
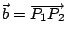
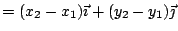 , ,
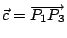
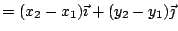 ,而 ,而
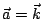 ,
則 ,
則
- [例4]平面方程式
設
P1(x1,y1,z1),
P1(x2,y2,z2),
P3(x3,y3,z3) 為空間中不共線三定點,
P(x,y,z) 為空間中任一點,則 P1,P2,P3 所決定之平面上,其充要條件為
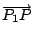 , ,
 , ,
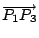 所張之平面六面體之體積為 0。換言之, 所張之平面六面體之體積為 0。換言之,
為P1,P2,P3所決定之平面方程式。
這個方程式還可以這樣看:
與
 及 及
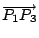 皆垂直,故為此一平面之一法線向量,
而此面又通過 P1 點,因此 皆垂直,故為此一平面之一法線向量,
而此面又通過 P1 點,因此
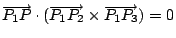 。 。
前面我們引進了
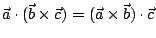 這種純量值的三重積,
現在我們考慮另一種向量值的三重積 這種純量值的三重積,
現在我們考慮另一種向量值的三重積
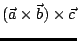 ,
我們可以證明 ,
我們可以證明
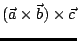 = =
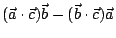 ,
從而Jacobi恆等式立即得證: ,
從而Jacobi恆等式立即得證:
這個式子,我們自然可以將
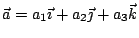 , ,
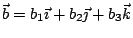 , ,
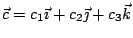 代入驗證。如果利用內積和外積的線性(分配律和混合結合律),當然簡化到只須檢查 代入驗證。如果利用內積和外積的線性(分配律和混合結合律),當然簡化到只須檢查 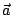 , ,
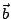 , ,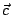 為座標單位向量 為座標單位向量
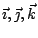 就夠。然而機械式的演算,到底難以深刻地瞭解與記憶,因此,我們從另一個角度來分析。 就夠。然而機械式的演算,到底難以深刻地瞭解與記憶,因此,我們從另一個角度來分析。
假設 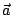 , ,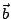 為二不平行的非零向量,則 為二不平行的非零向量,則
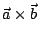 與 與 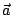 及 及 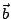 皆正交,
而 皆正交,
而
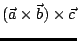 則又與 則又與
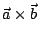 正交,
因此必須與 正交,
因此必須與 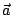 , ,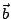 所張的平面平行,
也就是說 所張的平面平行,
也就是說
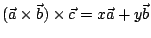 ,
又因 ,
又因
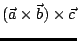 與 與 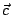 也正交,
故 也正交,
故
 。 。
若 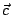 與 與 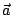 , ,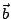 皆不正交,則有 皆不正交,則有
因此
在
 的特別情況時,不難看出 的特別情況時,不難看出 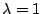 ,
也就是說 ,
也就是說
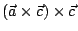
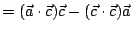 :
因為兩邊分別與 :
因為兩邊分別與 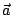 作內積,
則得 作內積,
則得
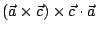
![$=\lambda \big[ (\vec{a}\cdot\vec{c})^2 -
(\vec{c}\cdot\vec{c})(\vec{a}\cdot\vec{a}) \big]$](img65.gif) ;
因此 ;
因此
即
從而 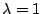 。 。
至於一般情況,
可將
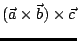

![$-(\vec{b}\cdot\vec{c})\vec{a}]$](img69.gif) 兩邊與 兩邊與 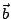 作內積而得: 作內積而得:
故 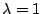 。 。
- [例5]
設 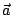 , ,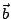 為二已知向量,且 為二已知向量,且 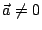 而 而
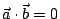 ,
又設 c 為一已知實數,試求一向量 ,
又設 c 為一已知實數,試求一向量 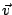 ,使其滿足 ,使其滿足
 。 。
- [解]
設 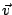 為所求之向量,則 為所求之向量,則
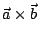
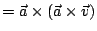

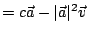 ,
故 ,
故
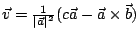 ,
代入檢驗,確實滿足。 ,
代入檢驗,確實滿足。
|
|
對外搜尋關鍵字:
.Hamilton
|

