熱力學中熵是一個極其重要的概念,最初由 Clausius 引進。
後來 L. Boltzmann 在他發表在1866年關於氣體動力學理論的開創性工作中給出了熵的另一形式。
這個熵在物理、化學的若干領域裡自始至終扮演著關鍵性的角色。
可是 Boltzmann 熵和我們先前定義的 Kolmogorov 熵或拓樸熵並非一致。
儘管如此,它們在數學的背景下,仍存在著千絲萬縷的聯繫。
在這最後一節,我們將遨遊於 Boltzmann 熵的數學描述。
設
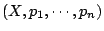 為一有限樣本空間,
則其 Shannon 熵為 為一有限樣本空間,
則其 Shannon 熵為
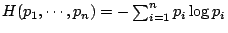 ,現設
,現設
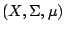 為一測度空間。
記 L'(X) 為定義在 X 上的 Lebesgue 可積函數全體。
L'(X) 中滿足等式 為一測度空間。
記 L'(X) 為定義在 X 上的 Lebesgue 可積函數全體。
L'(X) 中滿足等式
的非負函數了 f(x) 稱為密度函數,其集合記為 D。
易見等式
定義了 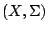 上的一個概率測度,其對應的密度就是 f(x)。
概率空間 上的一個概率測度,其對應的密度就是 f(x)。
概率空間
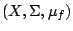 可看成是無窮樣本空間。
由 Shannon 熵的啟迪,我們可以如下定義 f 的 Boltzmann 熵。
為此,令函數 可看成是無窮樣本空間。
由 Shannon 熵的啟迪,我們可以如下定義 f 的 Boltzmann 熵。
為此,令函數 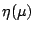 定義為 定義為
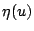 的圖像由圖4-1表示。 的圖像由圖4-1表示。
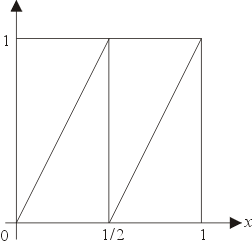
圖4-1
|
-
- 定義4-1:
- 設
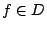 且 且
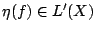 則 f 的 Boltzamann 熵定義為 則 f 的 Boltzamann 熵定義為
由 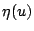 定義知, 定義知,
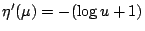 , ,
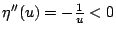 。因而η是 。因而η是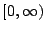 上的嚴格遞增凹函數,
由Taylor展式,任給 上的嚴格遞增凹函數,
由Taylor展式,任給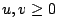 , ,
即,
簡化之,我們便有有名的 Gibbs 不等式,
任給函數 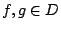 ,由 Gibbs 不等式和積分的單調性, ,由 Gibbs 不等式和積分的單調性,
由於
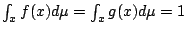 ,我們有如下重要的積分不等式: ,我們有如下重要的積分不等式:
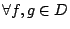
在有限的樣本空間 (X,p1,…,pn) 中,Shannon 熵在 p1=p2= … =pn=n 時為最大,Boltzmann 熵在概率測度空間裡也有類似的性質。
-
- 命題4-2:
- 設
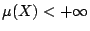 ,則密度函數 ,則密度函數
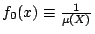 滿足
滿足
- 證明:
- 首先易見
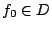 。其次,任給 。其次,任給 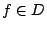 ,由不等式(4-1) ,由不等式(4-1)
為了描述一些與Boltzmann熵有關的條件極值問題。
我們引進一些概率論常用的術語。設X為一個隨機變量(Random Variable)
,即X為某一固定樣本空間上的可測實函數。
f(x)為這個測度空間的密度函數,則
稱為 X 的期望值 (Expected Value 或 Expectation)。
而數
則稱為 X 的變異數 (variance)。期望值是關於於隨機變量 X 平均值的一個度量,
變異數則表示隨機變量偏離其平均值的程度。下列性質,可以輕易的被驗證:
- (i)
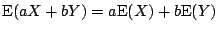
- (ii)
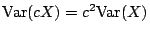
- (iii)
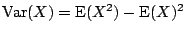
- (iv) 若 X 和 Y「獨立(independent)」則
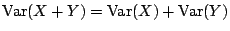
設有一列獨立隨機變量
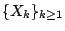 , ,
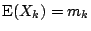 , ,
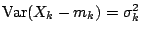 ,令 ,令
則,
我們標準化 Sn,即令
則
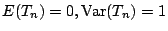
概率理論中有個非常重要的基本定理:中央極限定理
(central limit theorem)。它大概的意思是說,
在漸近狀態下,通常隨機變量 Tn 的概率分佈 (Probability distribution)
是遵循 Gauss 分佈規律的,也就是說,
其中 P 為樣本空間的概率分佈。
但是,為什麼大家都遵循的是 Gauss 分佈規律,而不是其他的分佈規律呢?事實上,
這和熱力學第二定律有異曲同工之妙。熱力學第二定律大致上說,自然界的規律是,一切動態系統都是在向「熵」高的方向發展。
從這個角度來看,在
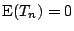 , ,
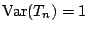 的條件下,
Gauss 分佈的確有最大的 Boltzmann 熵,我們用下面的命題,對這點略加說明。 的條件下,
Gauss 分佈的確有最大的 Boltzmann 熵,我們用下面的命題,對這點略加說明。
記
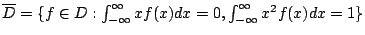
-
- 命題4-3
- 設
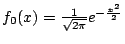 ,則 ,則 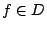 且 且
- 證明:
- 由公式
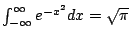 ,易知
,易知
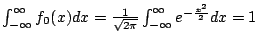 即
即 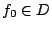 ,又由部分積分法易證 ,又由部分積分法易證
以及
則
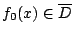 ,由不等式(4-1) ,由不等式(4-1)
類似地,記
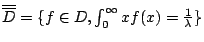 比照上述證明,我們有
比照上述證明,我們有
-
- 命題4-4:
- 設
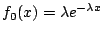 ,則 ,則
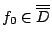 ,
且 ,
且
上述兩命題,可推廣到下述一般情形。設
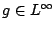 ,給定約束 ,給定約束
則H(f)在此約束下,最大值的密度函數應為
其中r為一常數。同樣,若有兩個約束
和
則密度函數
給出了H(f)在這兩個約束下的最大值H(f0),
其中r1,r2為兩常數。更一般地,我們有
-
- 命題4-4:
- 設
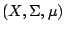 為一測度空間,非負函數 為一測度空間,非負函數
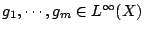 及正常數 r1,…,rm 滿足條件 及正常數 r1,…,rm 滿足條件
則 H(f) 在約束
下最大密度值函數為
- 證明:
- 為簡單起見,令
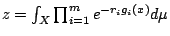 ,則 ,則
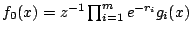 。
不難算出 。
不難算出
任給密度函數 f 滿足上述約束條件,由不等式(4-1)知,
特別,當 m=1 時,若 g(x) 看成是系統的能量時,
f0(x)= z-1 e-rg(x) 恰好就是 Gibbs 典型分怖函數,且
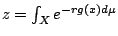 為其分析函數,而對應的最大熵 為其分析函數,而對應的最大熵
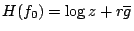 恰好就是眾所周知的熱力學熵。 恰好就是眾所周知的熱力學熵。
|