| |
我們再來做旋轉光滑硬幣的遊戲。為了方便起見,
我們稱硬幣的正面為 l,反面為 0。讓我們考察連續旋轉 n 次,
其每次正反面出現的各種可能性。旋轉一次,有兩個可能性,
或正面朝上,或反面朝上,即 1,0;旋轉兩次有 4=22 種可能性,
即 11,10,01,00;一般來說,旋轉 n 次則有 2n 種可能性。
把連續旋轉 n 次的任一可能結果看成一個「基本事件」,
我們則得到一個具有 2n 個基本事件的樣本空間,
其每一基本事件有同樣的概率 2-n。
上節中所談 Shannon 熵給出了這個樣本空閒的不確定度──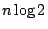 。
現在我們要進一步問的是:如果我們已知旋轉硬幣第一次,第二次,…
第 n-1 次的結果,那麼第 n 次會是正面或會是反面的不確定度該是多少? 。
現在我們要進一步問的是:如果我們已知旋轉硬幣第一次,第二次,…
第 n-1 次的結果,那麼第 n 次會是正面或會是反面的不確定度該是多少?
我們希望能用數學上的語言來描述這個問題。
首先讓我們來考慮定義在 [0,1] 上的函數
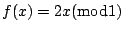 ,也就是 ,也就是
(見圖2-1),取 Lebesgue 測度 m 做為 [0,1] 上的測度,
令
![$\overline{A}=\{ [0,\frac{1}{2}],[\frac{1}{2},0] \}$](img61.gif) 為 [0,1] 上的一個劃分 (partition),
則
為 [0,1] 上的一個劃分 (partition),
則
![$f^{-1}(\overline{A})=
\{ f^{-1}([0,\frac{1}{2}]),f^{-1}([\frac{1}{2},1])\}$](img62.gif)
![$=\{ [0,\frac{1}{4}] \cup [\frac{1}{2},\frac{3}{4}],$](img63.gif)
![$[\frac{1}{4},\frac{1}{2}] \cup [\frac{3}{4},1]\}$](img64.gif) 也是 [0,1] 上的一個劃分。
任給兩個劃分
也是 [0,1] 上的一個劃分。
任給兩個劃分  和 和 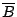 ,令 ,令
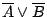 為由下式定義的劃分 為由下式定義的劃分
由此,我們則有
![$f^{-1}(\overline{A})\vee\overline{A}
=\{[0,\frac{1}{4}],[\frac{1}{4},\frac{1}{2},
[\frac{1}{2},\frac{3}{4}],[\frac{3}{4},1]\}$](img69.gif) 如此這般下去,我們會有
如此這般下去,我們會有
的劃分,這個劃分裡的每個區間
![$[\frac{i-1}{2^n},\frac{i}{2^n}]$](img71.gif) 都有 2-n 的 Lebesgue 概率測度。
事實上,它和旋轉硬幣 n 次那個樣本空間裡的 2n 個基本事件是一一對應的。 都有 2-n 的 Lebesgue 概率測度。
事實上,它和旋轉硬幣 n 次那個樣本空間裡的 2n 個基本事件是一一對應的。
拿 n=3 其中的一個簡單情況來看。把
![$[\frac{3}{8},\frac{4}{8}]$](img72.gif) 這個區間左端的 這個區間左端的 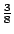 寫成 寫成
然後將
![$[\frac{3}{8},\frac{4}{8}]$](img72.gif) 這個區間和 011(第一次反面,第二次正面,第三次反面)對應。一般來說,我們可以把 這個區間和 011(第一次反面,第二次正面,第三次反面)對應。一般來說,我們可以把
![$[\frac{i-1}{2^n},\frac{i}{2^n}]$](img71.gif) 這個區間左端的 這個區間左端的
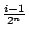 寫成
寫成
其中 ak=0 或 1, k=1,…,n。這個區間對應的是旋轉硬幣 n 次,
出現
 的基本事件。
總的來說,旋轉硬幣 n 次,2n 個基本事件,
大家的機率都是 2-n 的樣本空間,拿 的基本事件。
總的來說,旋轉硬幣 n 次,2n 個基本事件,
大家的機率都是 2-n 的樣本空間,拿
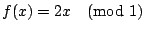 和劃分 和劃分
![$\overline{A}=\{ [0,\frac{1}{2}],[\frac{1}{2},1]\}$](img79.gif) 來描述,
則是:拿劃分 來描述,
則是:拿劃分
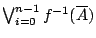 裡的 2n 個元素 裡的 2n 個元素
![$[\frac{i-1}{2^n},\frac{i}{2^n}]$](img71.gif) 做基本事件,
大家的 Lebesgue 概率測度都是 2-n 的樣本空間。 做基本事件,
大家的 Lebesgue 概率測度都是 2-n 的樣本空間。
「已知旋轉硬幣第一次,第二次,…,第 n-1 次的結果,
那麼第 n 次會是正面或反面的不確定度是多少?」
的這一問題,拿
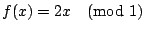 和劃分 和劃分
![$\overline{A}=\{ [0,\frac{1}{2}],[\frac{1}{2},1]\}$](img79.gif) 來描述,
事實上是在問:已知 x,…,fn-1(x)
在劃分 來描述,
事實上是在問:已知 x,…,fn-1(x)
在劃分  裡的位置,那麼 fn(x) 會在 裡的位置,那麼 fn(x) 會在
![$[0,\frac{1}{2}]$](img81.gif) 裡
或在 裡
或在
![$[\frac{1}{2},1]$](img82.gif) 裡的不確定度是多少呢? 裡的不確定度是多少呢?
讓我們來看 n=4 這個特殊情形。比如說我們已知前三次的結果,
它們是 101(第一次正面,第二次反面,第三次正面),這在
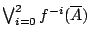 中所對應的區間是 中所對應的區間是
![$[\frac{5}{2^3},\frac{6}{2^3}]$](img84.gif) ,因為 ,因為
仔細的看,這個間區事實上是,
![$[\frac{1}{2},1]$](img82.gif) 和 和
![$f^{-1}([0,\frac{1}{2}])=$](img86.gif)
![$[0,\frac{1}{4}]\cup [\frac{1}{2},\frac{3}{4}]$](img87.gif) 以及 以及
![$f^{-2}([\frac{1}{2},1])=[\frac{1}{8},\frac{1}{4}]$](img88.gif)
![$\cup [\frac{3}{8},\frac{1}{2}] \cup [\frac{5}{8},\frac{3}{4}]$](img89.gif)
![$\cup [\frac{7}{8},1]$](img90.gif) 的交集,也就是說 的交集,也就是說
元素x在這交集所代表的意義是:
![$x \in [\frac{1}{2},1],f(x)\in [0,\frac{1}{2}]$](img92.gif) 和
和
![$f^2(x)\in [\frac{1}{2},1]$](img93.gif) 。
一般說來,已知前三次旋轉硬幣的結果相當於已知 x,f(x),f2(x)
在劃分 。
一般說來,已知前三次旋轉硬幣的結果相當於已知 x,f(x),f2(x)
在劃分
![$\overline{A}=\{ [0,\frac{1}{2}],[\frac{1}{2},1]\}$](img79.gif) 中的位置。
問第四次是正面還是反面的不確定度,相當於問 f3(x) 究竟是在 中的位置。
問第四次是正面還是反面的不確定度,相當於問 f3(x) 究竟是在
![$[0,\frac{1}{2}]$](img81.gif) 中還是在 中還是在
![$[\frac{1}{2},1]$](img82.gif) 中的不確定度。 中的不確定度。
已知
 在那裡,問 fn(x) 在那裡的不確定度,
當 n 趨近於無窮大時的變化就是我們在這一節要談的 Kolmogorov 熵。 在那裡,問 fn(x) 在那裡的不確定度,
當 n 趨近於無窮大時的變化就是我們在這一節要談的 Kolmogorov 熵。
我們將把我們的著眼點放在一般的概率測度空間 (Probability measure space) 和定義在它上面的可測變換 (measurable function)。
設
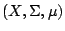 為一概率測度空間。即 X 為一集合,
Σ 為 X 上的一些子集合所構成的一個 為一概率測度空間。即 X 為一集合,
Σ 為 X 上的一些子集合所構成的一個  代數,
μ 為 Σ 上的概率測度,也就是說 代數,
μ 為 Σ 上的概率測度,也就是說 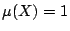 。
假設 。
假設
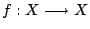 為一個可測變換。
這是指,Σ 中每個元素的逆像 f-1(A) 仍在 σ 中。
我們任取 X 的一個有限劃分 (finite partition) 為一個可測變換。
這是指,Σ 中每個元素的逆像 f-1(A) 仍在 σ 中。
我們任取 X 的一個有限劃分 (finite partition)
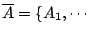 ,Am} 即 ,Am} 即
 中每個集合 Ai 屬於 Σ,
它們之間互不相交(交集的測度為 0)且聯集恰為 X。
這樣 中每個集合 Ai 屬於 Σ,
它們之間互不相交(交集的測度為 0)且聯集恰為 X。
這樣  可看成具有「基本事件」
A1,A2,…,Am 且有概率分布 可看成具有「基本事件」
A1,A2,…,Am 且有概率分布 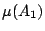 ,…, ,…,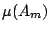 的一個有限樣本空間。這個樣本空間經常被稱為「試驗結果」。上節中談到,這個「試驗結果」的 Shannon 熵應為: 的一個有限樣本空間。這個樣本空間經常被稱為「試驗結果」。上節中談到,這個「試驗結果」的 Shannon 熵應為:
對給定的 f,集族
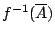
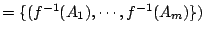 也可給出 X 的一個劃分。首先我們要提出這樣的問題:
在試驗結果
也可給出 X 的一個劃分。首先我們要提出這樣的問題:
在試驗結果
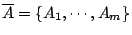 為已知的前提下,試驗結果
為已知的前提下,試驗結果
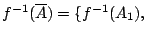 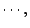 f-1(An)}
的不確定度為多少?也就是說,我們欲知:已知 x 在 Ai 中,
問 f(x) 在何處的不確定度為多少?
我們可以從條件概率的角度來探討之。為簡單起見,
設 n=3,即 f-1(An)}
的不確定度為多少?也就是說,我們欲知:已知 x 在 Ai 中,
問 f(x) 在何處的不確定度為多少?
我們可以從條件概率的角度來探討之。為簡單起見,
設 n=3,即
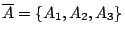 。
假如,已知 x 在 A1 中我們來看 f(x) 在 A1,A2 或 A3 的概率為如何。
對 。
假如,已知 x 在 A1 中我們來看 f(x) 在 A1,A2 或 A3 的概率為如何。
對
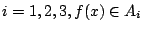 ,當且僅當 ,當且僅當
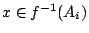 ,
故 x 在 A1 中且 f(x) 在 Ai 中之集合為 ,
故 x 在 A1 中且 f(x) 在 Ai 中之集合為
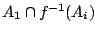 ,
因而其條件概率為 ,
因而其條件概率為
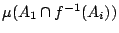 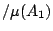 。
由 Shannon 熵的定義知,在 。
由 Shannon 熵的定義知,在 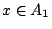 的條件下,
f(x) 會在 A1,或 A2,或 A3 的不確度應為 的條件下,
f(x) 會在 A1,或 A2,或 A3 的不確度應為
類似地,在 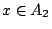 ,或 ,或 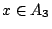 的條件下,試驗
結果 的條件下,試驗
結果
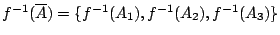 的不確定度應分別為
的不確定度應分別為
和
由推導 Shannon 熵定義的條件(ii)易知,
在試驗結果
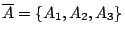 為已知的條件下,
試驗結果 為已知的條件下,
試驗結果
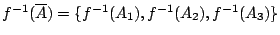 的不確定度 的不確定度
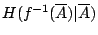 為H1,H2,H3的加權和,即
為H1,H2,H3的加權和,即
如法炮製,對一般的有限劃分
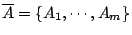 我們可得到所謂的「劃分
我們可得到所謂的「劃分
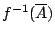 關於劃分 關於劃分  的條件 shannon 熵」,
的條件 shannon 熵」,
下面,我們來給出上述
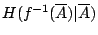 的另一等價型式以便後面推廣。 的另一等價型式以便後面推廣。
-
- 命題2-1:
-
- 證明:
-
命題2-1在直觀上看也很顯然:試驗結果
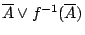 的不確定度
的不確定度
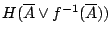 應為試驗結果 應為試驗結果 的不確定度
的不確定度
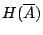 在試驗結果 在試驗結果 為已知條件下,
試驗結果 為已知條件下,
試驗結果
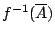 的不確定度 的不確定度
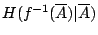 之和。
之和。
上述已知試驗結果 ,問試驗結果f-1(A)的不確定度,
相當於已知x在 ,問試驗結果f-1(A)的不確定度,
相當於已知x在 中的位置,
我們問f(x)在 中的位置,
我們問f(x)在 中的位置的不確定度。
已知 中的位置的不確定度。
已知
 在分劃 在分劃 中的位置,
問 fn(x) 在 中的位置,
問 fn(x) 在  中的位置的不確定度,
則相當於已知試驗結果 中的位置的不確定度,
則相當於已知試驗結果

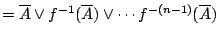 ,問試驗結果
,問試驗結果
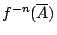 的不確定度。
Kolomogorov 熵基本上是在刻劃這個不確定度在當 n 趨近於無窮大時的漸近性質。 的不確定度。
Kolomogorov 熵基本上是在刻劃這個不確定度在當 n 趨近於無窮大時的漸近性質。
任給自然數n,
 和
和
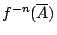 都是 X 的有限劃分。
在已知試驗結果, 都是 X 的有限劃分。
在已知試驗結果,
 的條件下,
試驗結果 的條件下,
試驗結果
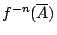 的不確定度,
實際上是劃分 的不確定度,
實際上是劃分
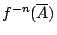 的條件 Shannon 熵,它是 的條件 Shannon 熵,它是
-
- 定義2-2:
- 設
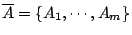 為
X的有限劃分,則可測變換 為
X的有限劃分,則可測變換
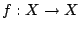 關於 關於 的熵定義為
的熵定義為
- 定義2-3:
- 設 (X,Σ,μ) 為一概率空間,
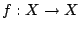 為一可測變換,
則 f 的 Kolomogorov 熵定義為 為一可測變換,
則 f 的 Kolomogorov 熵定義為
對一般的可測變換
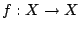 ,
上述定義2-2中的上極限符號不能改為極限符號。
但對遍歷理論中所研究的一類重要可測變換-保測變換
(measure preserving transformation)我們可以證明極限 ,
上述定義2-2中的上極限符號不能改為極限符號。
但對遍歷理論中所研究的一類重要可測變換-保測變換
(measure preserving transformation)我們可以證明極限
 確實存在並有一另一種等價定義。該定義顯然不及前者直觀易懂,
但它卻給出了計算上的許多方便。所謂保測變換是指
確實存在並有一另一種等價定義。該定義顯然不及前者直觀易懂,
但它卻給出了計算上的許多方便。所謂保測變換是指
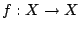 ,
任給 ,
任給 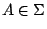 , ,
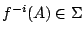 且有 且有
-
- 定義2-2:
- 設
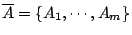 為 X 的有限劃分,
則保測變換 為 X 的有限劃分,
則保測變換
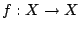 關於 關於 的熵定義為 的熵定義為
在證明此定義合理,且與定義2-2等價之前,我們首先注意到如下的事實:
若f為保測變換,則
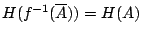 這由條件
這由條件
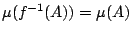 易見。
若 易見。
若 和 和 為X的兩個有限劃分,
我們記 為X的兩個有限劃分,
我們記
 ,若 ,若
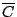 的每一元素是 的每一元素是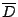 中某些元素之聯(Union)
(即 中某些元素之聯(Union)
(即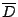 是 是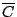 的一個細分(refinement))
我們需要下列引理,其證明稍後給出。 的一個細分(refinement))
我們需要下列引理,其證明稍後給出。
-
- 引理2-4:
- 若
 ,
則 ,
則
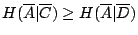
現在可以敘述並證明我們的等價定理了。
-
- 定理2-5:
- 若
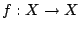 為保測變換,則對 X 的任一劃分 為保測變換,則對 X 的任一劃分 
- 證明:
- n=1,則
當 n=2 時,
用歸納法易證,一般地有
由上述引理2-4,故極限存在。從而,定義2-2中的極限實際上存在。
另一方面,對 i=1,2,…,n-1,由
各式相加,我們有
故有
借用初等微積分的已知結果:
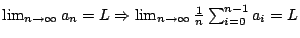 ,我們得到 ,我們得到
現在我們來證明引理2-4。
設
 , ,
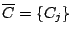 , ,
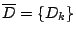 ,
我們要證 ,
我們要證
只須證明對每一 i 和 j
令
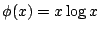 , , 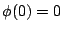 則上式為 則上式為
由於 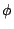 是凸函數(這由 是凸函數(這由
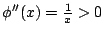 可知)
和假設 可知)
和假設
 ,易知 ,易知
即我們證明了
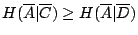
歷史上,引進 Kolmogorov 熵概念的主要動力是關於概率空間保測變換之間共軛關係的不變量的研究。
設
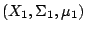 和 和
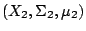 為兩個概率空間, 為兩個概率空間,
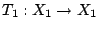 和 和
 為保測變換。
我們說 T1 和 T2 共軛 (conjugate) 是指存在一個保測同構 為保測變換。
我們說 T1 和 T2 共軛 (conjugate) 是指存在一個保測同構
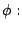
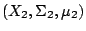 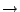
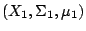 使得
使得
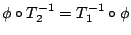 。
我們稱一個數量為共軛保測變換的「不變量 (invariance)」
是指二個保測變換若是共軛,這個數量一定一樣。
這個數量若不一樣,這兩個保測變換一定不共軛。
共軛的保測變換具有同樣的遍歷性質。
我們若能找到關於共軛保測變換的不變量,我們就可從本質上刻劃不同共軛類保測變換的特徵:Kolmogorov 熵就是這樣的一個重要的不變量。 。
我們稱一個數量為共軛保測變換的「不變量 (invariance)」
是指二個保測變換若是共軛,這個數量一定一樣。
這個數量若不一樣,這兩個保測變換一定不共軛。
共軛的保測變換具有同樣的遍歷性質。
我們若能找到關於共軛保測變換的不變量,我們就可從本質上刻劃不同共軛類保測變換的特徵:Kolmogorov 熵就是這樣的一個重要的不變量。
早在1943年,人們就知道 Bernoulli 的 (
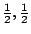 )
-雙邊移位算子 (two side shift) 和
( )
-雙邊移位算子 (two side shift) 和
(
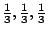 )-
雙邊移位算子都具有可數個 Lebesgue 譜點,因而是譜同構的,但不知道它們是否共軛。
直到1958年才由 Kolmogorov 證明了它們分別具有 )-
雙邊移位算子都具有可數個 Lebesgue 譜點,因而是譜同構的,但不知道它們是否共軛。
直到1958年才由 Kolmogorov 證明了它們分別具有  和 和 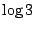 的
Kolmogorov 熵,故非共軛。從而消除了遍歷理論這個重大懸念,並開創了一個嶄新的研究領域。
我們這裡介紹的 Kolmogorov 熵的概念是由 Kolmogorov 的學生 Sinai 在1959年改進的,和 Kolmogorov 1958年給出的原始定義稍有不同。 的
Kolmogorov 熵,故非共軛。從而消除了遍歷理論這個重大懸念,並開創了一個嶄新的研究領域。
我們這裡介紹的 Kolmogorov 熵的概念是由 Kolmogorov 的學生 Sinai 在1959年改進的,和 Kolmogorov 1958年給出的原始定義稍有不同。
|
|
|