斯坦納二重奏 (第 3 頁)

　1│2│3│4│5│6　

斯坦納二重奏
斯坦納系和斯坦納樹（第 3 頁）

黃光明

首頁 | 搜尋

．原載於數學傳播十卷一期
．作者當時任職於美國電話公司貝爾實驗室
‧對外搜尋關鍵字

三、斯坦納系樂章

一個 (v,b,r,k,λ) 設計，也稱區組設計 (block design)，指的是 v 元集 V 上由 b 個 k-子集（每一 k-子集也稱一區組）組成的一個子集族。它滿足下列兩條件：

(甲) V 的每個元素恰出現在 r 個區組中。
(乙) V 的每一對元素恰出現在 λ 個區組中。

下例是一個 (6,10,5,3,2) 設計：

$\begin{displaymath} \begin{array}{l} \{2,3,6\},\{1,3,4\},\{3,4,5\},\{2,4,5\},\{3... ... \{1,4,6\},\{1,5,6\},\{1,2,3\},\{2,4,6\},\{1,2,5\} \end{array}\end{displaymath}$

元素 1 出現在區組 2,6,7,8,10 中共五次，其他元素也各出現五次，元素 1 和 2 共同出現在區組 8，10中共二次，其他任二元素亦同出現二次。
在一個 (v,b,r,k,λ) 設計中，v 個元素每個出現 r 次，所以共出現 vr 次。另一方面，b 個區組每一個中有 k 個元素出現，所以共出現 bk 次，因此

$\begin{displaymath} vr=bk \eqno{(1)} \end{displaymath}$

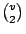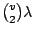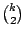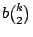v 個元素共有 ${v \choose 2}$ 對，每對出現 λ 次，所以共出現 ${v \choose 2} \lambda$ 對次。另一方面 b 個區組每一個中有 ${k \choose 2}$ 對出現，所以共出現 $b {k \choose 2}$ 對次。因此

$\begin{displaymath} {v \choose 2} \lambda = b {k \choose 2} \eqno{(2)} \end{displaymath}$

所以 v,b,r,k,λ 五個參數中事實上只有三個獨立參數，設為 v,k,λ。由(1)和(2)解得

$\begin{displaymath} r=\frac{\lambda(v-1)}{k-1} \end{displaymath}$

及

$\begin{displaymath} b=\frac{\lambda v(v-1)}{k(k-1)} \end{displaymath}$

由於 r 和 b 必須是整數，故知

$\begin{displaymath} \begin{eqalign} \lambda(v-1) &\equiv 0 \pmod{k-1} \\ \lambda v(v-1) &\equiv 0 \pmod{k(k-1)} \end{eqalign}\eqno{(3)} \end{displaymath}$

是 (v,b,r,k,λ) 設計存在的必要條件。問題是(3)是否也是充分條件？

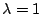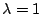讀者很容易自行檢驗當 k=1 和 2 時，唯一的區組設計分別是 V 的全部 1-子集和 V 的全部 2-子集。這兩種平凡情形一筆帶過即可。 k=3 時是第一個需要研究的情形，而 k=3 的情形仍需一步步做。第一步是解決 $\lambda = 1$ 的問題。注意當 k=3， $\lambda = 1$ 時，(3)可簡化為

$\begin{displaymath} v \equiv 1 \mbox{ {\fontfamily{cwM1}\fontseries{m}\selectfont \char 67} } 3 \pmod{6} \eqno{(4)} \end{displaymath}$

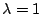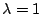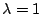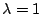英國的伍爾豪斯 (Woolhouse) 在1844年首先提出 k=3, $\lambda = 1$ 的區組設計問題，三年後同為英籍的柯克曼 (Kirkman) 牧師證明了(4)式的確是 (v,b,r,3,1) 設計存在的充要條件。但基於「好事不出門，惡事傳千里」的原則，這一發現並未傳到海峽對岸的歐洲大陸。 1853年斯坦納「閉門家中坐」在研究四次曲線的二重切線問題時也遇到了 k=3， $\lambda = 1$ 的區組設計問題，他猜測了六年前柯克曼已證明了的結果，1859年賴斯 (Reiss) 證明了斯坦納的猜測。從此，k=3, $\lambda = 1$ 的區組設計就被稱為斯坦納三元系 (triple system)。一個名稱一被發明後就無孔不入，因此 k=3, λ 一般的區組設計就叫做三元系，而 k 一般， $\lambda = 1$ 的區組設計當然順理成章的叫斯坦納系。

區組設計存在的充要條件這一問題一直到一百年後才獲得了重大的突破。 1961年猶太人哈納尼 (Hanani) 證明了(3)式確是三元系區組設計存在的充要條件，他也證明了(3)式也是 k=4 時的充要條件。但當 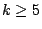$k\geq 5$ 時人們早就知道有些滿足(3)式的區組設計並不存在，因此提出下一猜想：「對給定的定 k，除去有限對數值 (v,λ) 之外， (3)式是區組設計存在的充要條件。」 1975年美國人威爾遜 (Wilson) 證明了這一猜想，一百三十年來這一問題在組合學界引起的波動與震撼，至此塵埃落定。

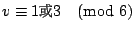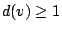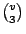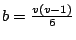在組合學的研究上往往在解決了存在的問題後下一個要回答的問題是有多少？因此我們也可以問對於一個給定的正整數 v，究竟有多少個不同的斯坦納三元系存在？這個問題也許太難了，我們把範圍收歛一點。如果在同一個 v 元集上的兩個斯坦納三元系沒有相同的區組，則我們說這兩個三元集不相交。定義 d(v) 為給定 v 後互不相交的斯坦納三元系最大的數目，對於 d(v) 的探討稱為斯坦納三元系大集 (large set) 問題。從斯坦納三元系的充要條件我們只需討論 $v\equiv 1 \mbox{{\fontfamily{cwM1}\fontseries{m}\selectfont \char 67}} 3 \pmod{6}$ 的情形，且已知 $d(v)\geq 1$ 。另一方面，V 共有 ${v \choose 3}$ 個 3-子集，而每一個斯坦納三元集含 $b=\frac{v(v-1)}{6}$ 個 3-子集，故知

$\begin{displaymath} d(v)\leq \frac{ {v \choose 3} }{b}=v-2 \end{displaymath}$

如果 d(v)=v-2，我們說對於這一 v 值，斯坦納三元系大集存在。

大集問題的誕生幾乎和斯坦納三元系同時。 1850年英國大數學家凱萊 (Cayley) 證明了 d(7)=2，即大系只包含 D1 和 D2 兩設計：

$\begin{displaymath} D1: \begin{array}{l} \{1,2,3\},\{1,4,5\},\{1,6,7\},\\ \{2,4,6\},\{2,5,7\},\{3,4,7\},\{3,5,6\} \end{array}\end{displaymath}$

$\begin{displaymath} D2: \begin{array}{l} \{1,2,7\},\{1,3,4\},\{1,5,6\},\\ \{2,3,6\},\{2,4,5\},\{3,5,7\},\{4,6,7\} \end{array}\end{displaymath}$

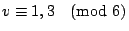同年柯克曼證明了 d(9)=7。但不像斯坦納三元系在數年內即分別被柯克曼和賴斯解決，大集問題在下一百年內幾乎毫無進展，由此可以看出它的難度。一直到1972年始，多延 (Doyen)，考席 (Kotzig)等從尋求 d(v) 的下界入手，引進遞歸方法，才使這個問題有了新的進展。 1973年和1974年丹尼斯頓 (Denniston)，施賴伯 (Schreiber) 和威爾遜陸續對 205 以內，滿足 $v\equiv 1,3 \pmod{6}$ 的大部份 v 值給出了斯坦納三元系大集。此外泰爾林克 (Teirlinck) 和羅莎 (Rosa) 分別給出了 v 到 3v 和 v 到 2v+1 的遞歸結果。但是總而言之到1980年止，關於斯坦納三元系大集的存在問題只有零碎的結果而無全面破案之計。

我們現在把鏡頭自北美大陸迅速拉開，越過太平洋，越過山東半島，越過華北平原而到達內蒙古境內，可以聽到黃河，可以望見長城的包頭市。在這兒的包頭九中一位年輕的物理老師陸家羲，在六十年代初期即在繁忙的物理教學課後，埋頭從事他業餘興趣，組合設計研究。六十年代初期正是組合學的輝煌時代，1960年玻色 (Bose)、血汗 (Shrikhande)，派克 (Parker) 粉碎了歐勒 (Euler) 在拉丁方陣上的猜想，第一次把數學帶上了紐約時報的頭版。 1961年哈納尼獲得了 k=3,4 時區組設計的充要條件，這些都是組合學上百年來的大事。陸家羲1961年解決了在組合學上號稱三大疑案之一的「柯克曼女學生」問題，他的文章投寄給中國的數學雜誌，卻遭到屢投屢退的命運，現在他的原稿已經遺失，只留下了投稿退稿的記錄，及1965年的修正稿。這份修正稿的正確性現已由蘇州大學的吳利生教授肯定，當年卻仍不能受到審稿者的青睞。在中國明珠被藏的時候，國外的學者卻在生氣勃勃的叩關攻堅。 1971年美國俄亥俄州大的博士生威爾遜和他的導師印籍雷小杜里 (Ray-Chaudhuri) 終於接受著大家的恭賀成為「柯克曼女學生」問題的法定征服者。

然後是四人幫的混沌時期，學校關閉，教師下放，除了少數親朋外全世界大概沒有人知道陸家羲的下落也沒有人會關心。像中國眾多的年輕科學家，有發光的潛能，有發熱的內涵，卻因命運的播弄而含苞未放，像天際一顆遙遠的星星在人們還來不及注意它時已被厚黑的雲層吞沒。

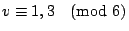吞沒了嗎？在下一個浪潮中陸家羲卻又平地一聲雷的站了起來。隨著中國大陸的對外開放政策，陸家羲這次越過了中國的障礙而把研究成果投寄到美國頗有權威性的「組合論雜誌」。從1981到1983年，該雜誌先後發表了陸家羲六篇論文，宣佈了斯坦納三元系大集問題的徹底解決。他證明了當 $v\equiv 1,3 \pmod{6}$ 且 v>7 時除了

$\begin{displaymath} v\in \{141,283,501,789,1501,2365\} \end{displaymath}$

六個數外，d(v) 恆等於 v-2。這一顆曾被柯克曼、凱萊、西爾威斯特 (Silvester) 等數學界大賢灌溉過的鐵樹，終於百年後在陸家羲的手上開了花。

對於六個沒有答案的 v 值，陸家羲也在1983年的數學會議上宣佈了他已明珠在握，將寫成第七篇論文。可惜同年十月陸家羲在寫下了二十四頁的綱領後，即突然去世了，留待後人來舉起他苦撐四分之一世紀積成疾放下的火炬。

　1│2│3│4│5│6　


	（若有指正、疑問……，可以在此留言或寫信給我們。）

EpisteMath (c) 2000 中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有

編輯：蔡宇軒

最後修改日期：5/6/2002