| |
假想一個粒子在水平直線上一步步的左右移動而且每步的距離皆為一個單位長;其向右及向左的機率各為 p 與 q=1-p (0<p<q)。此外,我們假設每一單位時間只移動一步而且第 n 步在第 n 個瞬間獨立做動作。若視直線為 R1 而視一個單位長為 1(向右一步以 +1 表示,向左一步以 -1 表示),則此粒子在 R1 上之可能位置為整數,其數學模式描述如下:
設 Xn 為粒子第 n 步的位移,則 {Xn:
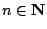 } 為一族取值 {+1,-1} 的獨立隨機數,而且對任一整數 } 為一族取值 {+1,-1} 的獨立隨機數,而且對任一整數 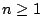 , ,
若以 W0 表粒子之原始位置,則在時間 n 時粒子的位置為
此一序列的隨機變數 {Wn:
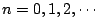 } 便叫做隨機漫步。{Wn} 所在的樣本空間 Ω 可取為 } 便叫做隨機漫步。{Wn} 所在的樣本空間 Ω 可取為
然後定義
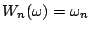 。當 。當
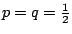 時,我們稱 {Wn} 為隨機漫步。以下我們概述隨機漫步的幾個基本性質。 時,我們稱 {Wn} 為隨機漫步。以下我們概述隨機漫步的幾個基本性質。
令 Prn(i,j)=
P{Wn+r=j|Wn=i},Pn(i,j)=P1n(i,j),
pij=P0(i,j),prij=Pr0(i,j)。
顯然,當 i=j 時 p0ij=1,否則 p0ij=0。
- 定理一:
-
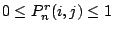 ,而且 ,而且
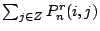 =1 =1
-
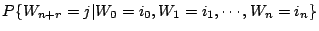
=
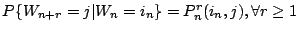 。 。
- Prn(i,j)=Pr0(i,j)=prij,
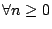 ,特別地, ,特別地,
- 設
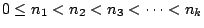 ,則
{Wnk-Wnk-1,…,Wn2-Wn1} 為獨立隨機變數 ,則
{Wnk-Wnk-1,…,Wn2-Wn1} 為獨立隨機變數
定理一之(1)顯然成立。(2)說明了當「現在」(指時間 n)之位置為已知時,則「過去」(指小於 n 之時間)與「未來」(指時間 n+r)無關。此性質稱為馬可夫性質 (Markov Property)。因此隨機漫步為一馬可夫過程。性質(3)表示粒子之位置從 i 轉移至 j 的機率與原位置之時間無關,此性質叫時間齊一性 (time-homogeneous)。
pij 叫做隨機漫步的轉移機率 (transition probability)。
(4)的性質是因 {Xn} 為獨立隨機變數之故;
由於該性質我們 {Wn} 具有獨立增量 (independent increments)。
- 系一:
- 令 P=(pij) 為 pij 所成之矩陣。P 稱為轉移矩陣或轉移函數。則
此外,
pnij = Pn(i,j)。
令
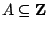 。定義 。定義
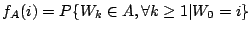 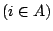 。fA(i) 表示 {Wn} 從 A 中之點 i 出發一直留在 A 中之機率。 。fA(i) 表示 {Wn} 從 A 中之點 i 出發一直留在 A 中之機率。
- 定理二:
- 若 A 只包含有限個整數,則 fA(i)=0,
 。 。
- 證明:
- 我們只證明
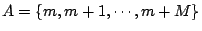 的情形就足夠了。令 Q 為由矩陣 P 去掉不在 A 中之行列後所形成的矩陣,顯然, 的情形就足夠了。令 Q 為由矩陣 P 去掉不在 A 中之行列後所形成的矩陣,顯然,
對  , ,
令
 。
由(2.1)得知 。
由(2.1)得知
而且
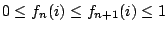 , ,
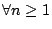 ,
故 ,
故
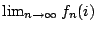 存在且其值恰為 fA(i)。
又由於
Qn+1 = QQn,我們有 存在且其值恰為 fA(i)。
又由於
Qn+1 = QQn,我們有
在(2.2)中,令
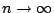 得 得
設
xi = fA(m+i), i=0,1,2, ,M,由(2.3),(xi) 滿足以下聯立方程組 ,M,由(2.3),(xi) 滿足以下聯立方程組
由(2.4)前 M 個方程式解得
特別地,
但是由(2.4)最後的等式,我們又得到
比較(2.6)與(2.7)得 x0=0,故由 (2.5)得 xi=0, 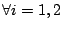 ,…,M。
所以 fA(i)=0, ,…,M。
所以 fA(i)=0,
 。 。
定理二說明了作隨機漫步的粒子非常「不安於位」,此性質與布朗運動粒子相似(見定理四之(3))。
以下我們只討論 {Wn} 為對稱的情形,而且我們讓所有的隨機漫步皆從原點開始,也就是說 W0=0。
- 定理三:
- E
[Wn+k|Wn=i]=
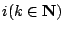 。 。
- 證明:
-
定理三說明了當粒子進行隨機漫步中,某甲在時間n時開始觀察,剛經過 k 時間後,粒子的預期位置為某甲開始觀察的位置 Wn。當 i 任意變動時,定理三可改寫為 E
[Wn+k|Wn]=Wn。
若我們把 Wn 看作某賭徒在時間n時身上所有金錢總數,則照定理三的意思,該賭徒在時間 n 時帶著 i 元進入賭場參與賭博,而 k 時間後,該賭徒應是不輸也不贏的帶著 i 元離去。因此,定理三之性質又稱平賭性質 (martingale property)
(martingale 是法國民間一種公平的對局)。下一節我們將發現布朗運動也是一種平賭過程,從隨機漫步的軌跡來看,我們可視隨機漫步為布朗運動離散化之情形,它的確可幫助我們了解布朗運動。
|
|
|