| |
�ڭ̭����Q�צb���ΤU
���F�Ϥ������u�����v�_���A�ڭ̧Ʊ�
�_�h
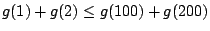 �N�S���Ӧh�����ȤF�C�q�Y��ƪ��ʽ�A�Y�ڭ̥i�H���@�� �N�S���Ӧh�����ȤF�C�q�Y��ƪ��ʽ�A�Y�ڭ̥i�H���@�� 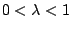 �A�B �A�B
�h(6)�P(7)����M���ߡA�q��2���A(8)������ y1,y2 �� x1 �P x2 �n���ǡC

��2
|
���n��ϧ�2���u���v�[������ n �תŶ��A�Y�� n �Ӥ��q���V�q(x1,x2,�K,xn) �� (y1,y2,�K,yn) �N���Ӯe���F�C���������Ϋ���M�AĴ�p��

��1
|
�h�ѹ�3�ݥX (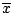 , ,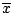 ,�K, ,�K,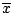 ) ��M�� (y1,y2,�K,yn) �n���C
�]�ӧڭ̦���(4)���A�Y ) ��M�� (y1,y2,�K,yn) �n���C
�]�ӧڭ̦���(4)���A�Y
�����Q��F�o�ˤ@�Ӥ����V�q X=(x1,x2,�K,xn)�AY=(y1,y2,�K,yn) ���ʪ���k�C
-
- �w�q:
- �O X = (x1,x2,�K,xn)�AY = (y1,y2,�K,yn) ���⺥��ǦC�A�Y
�B
�ڭ̻�X�i�H�u�\�o���vY�A��Y��X����A�p�G
�@��ڭ̥� Y<X ���ܤ��C
�ڭ̩ұĪ��w�q���u�A�Ω��Ӻ���ǦC�A���b�@�뱡�ΤU���������A�X�G���P�ǦC x1,x2,�K,xn, y1,y2,�K,yn ���ƦC�L���F�ҥH�ڭ̩ұĪ��w�q�ä�����@��ʡC�|�ӨҤl�AX=(3, 2, 1),
Y=(2.5, 2.3, 1.2)�A�h
3+2+1=2.5+2.3+2.1
�B
�G Y<X�C
�S����M��
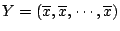
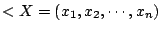 �CŪ�̤����ո��ҩ����@�ƹ�C�]�H��\�h�a��n�Ψ즹�@�ƹ�^ �CŪ�̤����ո��ҩ����@�ƹ�C�]�H��\�h�a��n�Ψ즹�@�ƹ�^
- ��:
- �ڭ̦b�夤���ɧ� (x1,x2,�K,xn) �H�ǦC�ݤ��C
���ɤ]��
 �A���V�q�ݤ��C�b���ǦC�ݮɡA
x1,x2,�K ���i�٬������A�b���V�q�ݮɡAx1,x2,�K ���H���q�٤��C
�ڭ̺� X �� Y ����Ӥ����Τ��q�ۦP�ɡA�O���F�ƭȥ����~�A�B�㦳�ۦP�����ǩΦ�m�C�Ҧp (3,2,1,5,3) �� (3,1,2,5,3) ��V�q�� 3 �露���ۦP�C �A���V�q�ݤ��C�b���ǦC�ݮɡA
x1,x2,�K ���i�٬������A�b���V�q�ݮɡAx1,x2,�K ���H���q�٤��C
�ڭ̺� X �� Y ����Ӥ����Τ��q�ۦP�ɡA�O���F�ƭȥ����~�A�B�㦳�ۦP�����ǩΦ�m�C�Ҧp (3,2,1,5,3) �� (3,1,2,5,3) ��V�q�� 3 �露���ۦP�C
�U�����w�z��\���[���P�Y��ƪ����Y���F�@�Ӥu�C
-
- �w�z4
- �OX=(x1,x2,�K,xn),Y=(y1,y2,�K,yn)�����ƦC�A�BX�PY�u����Ӥ������ۦP�A�]���m�bi��j�W(�Yxk=yk���Dk=i��k=j)�A�h�U�C����(i)�P(ii)�����R�n����C
- (i)Y<X
- (ii)���@�ӹ�ƣ\;
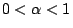 �B �B
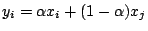 , ,
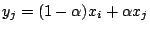
- ��:
- �]i�Pj�i�������m�C�]���ڭ̤������]
�ڭ̥���(i)���ɥX(ii)�C�]���F�b i,j ��m�W�������ҬۦP�A�S Y<X�A
�h������
��Y
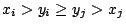 �C�Y�O �C�Y�O
�h 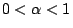 �ëܮe���ѥN�J �\ ���Ȧ��ұo(ii)�C �ëܮe���ѥN�J �\ ���Ȧ��ұo(ii)�C
�{�Y(ii)���ߡC�h�ѩ�bi���e��x,y�Ҭ۵��A�G��k<i�Ө�
�S�b k=i ��
�o�ؤ��������Τ@���� 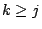 �ɤS��_�F�����]�]��
yi+yj=xi+xj�^�A�G���w�z�o�ҡC �ɤS��_�F�����]�]��
yi+yj=xi+xj�^�A�G���w�z�o�ҡC
-
- �w�z5
- �]��ƦC
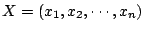 �A �A
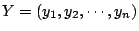 ���AX �P Y �����ۦP�åB Y<X�A
�h�ڭ̥i���@�ӼƦC Z=(z1,z2,�K,zn) ��ƤU�C�T�өʽ�: ���AX �P Y �����ۦP�åB Y<X�A
�h�ڭ̥i���@�ӼƦC Z=(z1,z2,�K,zn) ��ƤU�C�T�өʽ�:
- (1) Y<Z<X(�YY<Z,Z<X)
- (2) Z�PY��X�PY�ܤ֦h�@�ӬۦP������
- (3) Z�PX�ܦh�u����Ӥ������P�C
- ��:
- �]���w�z���ҩ��P X,Y ���������ƦC�L���A�������w X,Y �w������ƦC�A
�Y
�] Y<X�A�G
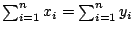 �A�S�] xi �P yi �����ۦP�A
�����@�� k �ϱo xk>yk �Τ@�� l �ϱo xl<yl�A�� i ���̤j�� k �� xk>yk ���ʽ�̡A
j ���̤p�� l>i �ú��� xl<yl �̡A�h X,Y�A�P i,j �����Y�p�U�G �A�S�] xi �P yi �����ۦP�A
�����@�� k �ϱo xk>yk �Τ@�� l �ϱo xl<yl�A�� i ���̤j�� k �� xk>yk ���ʽ�̡A
j ���̤p�� l>i �ú��� xl<yl �̡A�h X,Y�A�P i,j �����Y�p�U�G
�Y�� k=i+1,i+2,�K,j-1 �� yk=xk(�_�h i �i�V�k���� j �V�����P�Ҩ��� i �� j �ʽ褣��)�A
�S xt>yt,
 ��ys>xs, ��ys>xs,
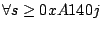 �C�O �C�O
�ѩ�
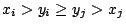 �A�i�� �A�i�� 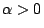 �A�� �A�� 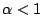 �C
�O zk �P xk �� k=i,j �ɬҬۦP�A�S �C
�O zk �P xk �� k=i,j �ɬҬۦP�A�S
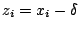 , ,
 �C�� �\ ���w�q�A�i�o �C�� �\ ���w�q�A�i�o
�ѩw�z3�o�� Z<X�A�] Z �P X ���F i,j ��m�W�������~�A�ҬۦP�A�G�ܮe���D�X
��
�G Y<Z�A�Y(1)�o�ҡC�ھ� �_ ���w�q�A�Y
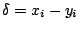 �hzi=yi�A�Y �hzi=yi�A�Y
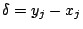 �hzj=yj�A�G(2)���ߡC�]X�PZ��i�Aj
��m�~���ۦP�A(3)��]���ұo�C
�hzj=yj�A�G(2)���ߡC�]X�PZ��i�Aj
��m�~���ۦP�A(3)��]���ұo�C
-
- �t�z:
- �̤W���w�z�A�ڭ̥i�H��� z1,z2,�K,
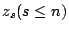 �ӼƦC�A�ϱo �ӼƦC�A�ϱo
(1)
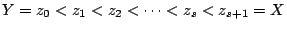
(2)�Ҧ�zi�Pzi+1����(
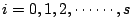 )�ܦh����Ӥ��P�������C )�ܦh����Ӥ��P�������C
- ��:
- �] X �P Y �ܦh���� n �Ӥ��P�������A�ѤW�w�z(2)����
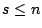 �C �C
�{�b�ڭ̥i�H�ԭz���ҩ����g�̥D�n�����G�F�C
-
- �w�z6(�����w�zSchur's Theorem)
- �] f(x) ���϶� [a,b] �W���@�Y��ơA�S X=(x1,x2,�K,xn), Y=(y1,y2,�K,yn) ����ƦC�A
�䤸���Ҧb [a,b] ���A�Y Y<X �h
- ��:
- �ѩw�z5���t�z�A�ڭ̥u���ҩ� Y �P X �u����Ӥ������ۦP�����δN��F�C�]�_�h�ڭ̥i�� z1,z2,�K,zs �@�����U�h�^
�O xi,xj �P yi,yj �U���ۦP�Ө�l�� x,y �ҬۦP�A�h(9)�ܦ��F
�] Y<X�A�G�ѩw�z4���A�ڭ��`�i���@�� �\, 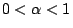 �B �B
�� f ���Y�ʽ�A�ڭ̦�
�G(10)�����ߡC�w�z6�]���o�ҡC
�{�b�ڭ̬ݬݩw�z6���@�ǥγ~�C
-
- ��1�G
- �O
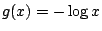 , , 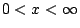 ���@�Y��ơA�S�Ѩƹ� ���@�Y��ơA�S�Ѩƹ�
�G�ѩw�z6�i�o
�Y
�o�N�O��N�����j��X�����ҩ��C
- ��2�G
- x1,x2,�K,xn �� n �ӥ��ơA
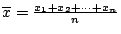 �A�h�] �A�h�]
 �� ��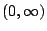 �W���@�Y��ơA�G�� �W���@�Y��ơA�G��
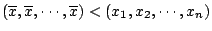 �Ωw�z6�i�o �Ωw�z6�i�o
�Y
- ��3�G
- �] x1,x2,�K,xn ������ 0<xi<1;
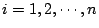 �� n �ӼơA�B �� n �ӼơA�B
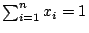 �A�h �A�h
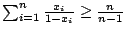
- ��:
- �ڭ̥���
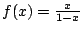 �b (0,1) �����Y��ơA�ڭ̥u������ �b (0,1) �����Y��ơA�ڭ̥u������
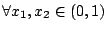
���۵���
��²�o
�����ڦ��ߡA�G f ���@�Y��ơC
�S�]
 �� ��
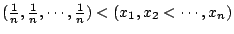 �ѩw�z6�i�o
�ѩw�z6�i�o
�Y
- ��4�G
- �] xi,
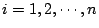 �� n �ӹ�ơAa ���@�w�ơC�O �� n �ӹ�ơAa ���@�w�ơC�O
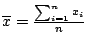 ���� ����
- ��:
- ��M�ѹϧΥi��f(x)=|x-a|���@�Y��Ƥ�
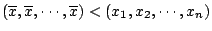 �A�̾کw�z6�즡�ߧY�o�ҡC
�A�̾کw�z6�즡�ߧY�o�ҡC
- ��5�G
- �]
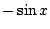 �b�϶� (0,�k) �������Y��ơA�S�b�@�T���Τ��A�Y�H A,B,C ���T�����A�h�ܮe���o�� �b�϶� (0,�k) �������Y��ơA�S�b�@�T���Τ��A�Y�H A,B,C ���T�����A�h�ܮe���o��
�G�ѩw�z6�i�o
�Y
�P�z�i�ұo
- ��6�G
- �O
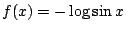 , , 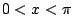 �h f(x) ���Y��ƪ����ץi�� �h f(x) ���Y��ƪ����ץi��
�Y�ƹ�
�S�ѩ�
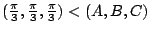 �̩w�z6�i�o �̩w�z6�i�o
�Y
�����w�z�����Υi�H���s��ܦh�W�X���g�{�ת��������A���\�h�O�b�έp�B�x�}���譱�����ΡC�ڭ̤��b���h�@���СC�Ʊ�Ū�̯�q���g�o��}�һ\�z���_�w���_�͡A�i�ӯ�藍�����z�ק@��`�J���s���ΰ^�m�C
- 1. G.H. Hardy, J.E. Littlewood, and G. Polya,�mInequalities�n, Cambridge University Press,1934.
- 2. A. Marshall and I. Olkin,�mInequalities: Theory of Majorization and its Applications�n, Academic Press, 1979.
|
|
|